Аннотация
Лопатина А. А., Еркаев Н. В. - Математическое моделирование колебаний балки мостового крана. Построение математическая модель колебаний балки с переменной массой и нагрузкой.
Общая постановка проблемы
Краном мостового типа называется кран с грузозахватным устройством, подвешенным к грузовой тележке, которая перемещается по подвижной стальной конструкции (мосту). Этот кран активно применяют в области строительства, в цеховом производстве, в заводском производстве и на складских терминалах.

Рисунок 1 – Кран мостовой двухбалочный.
Создание перспективных конструкций мостовых кранов требует хорошей проработки информации по конструкциям и параметрам мостовых кранов, разновидности конструкции, узлов и деталей, а также расчета поведения конструкции на определенное воздействие нагрузки в заданный момент времени. Установлено, что перемещения балки мостового крана могут быть описаны дифференциальным уравнением движения балки, нагруженной распределенной нагрузкой:
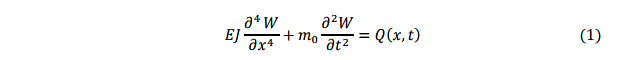
Здесь ЕJ- изгибная жесткость материала, m0 - масса единичного участка, Q(x,t) - сила тяжести тележки.
Вводим безразмерные переменные:


Получим уравнение в виде:
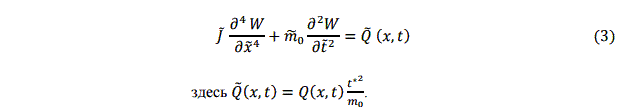
В дальнейшем мы рассматриваем только безразмерное уравнение колебаний, и знак волны над безразмерными переменными опускаем для простоты.
Для построения конечномерной модели балки используем уравнение Лагранжа второго рода:
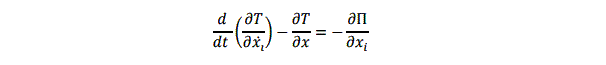
где T - кинетическая энергия, П – потенциальная энергия, которые нашем случае равны:

Применяя конечноразностную аппроксимацию, разбиваем балку на N равных участков и записываем кинетическую и потенциальную энергии в виде конечных сумм:

Здесь Δl- длина малого участка разбиения, равная 1/N
Подставляя выражения кинетической и потенциальной энергий в уравнение Лагранжа, получаем конечномерные уравнения:
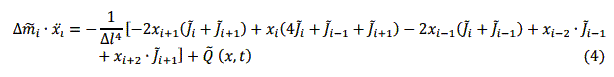
Здесь индекс i – номер участка разбиения.
Система уравнений (4) интегрировалась численно с использованием пакета MATHCAD для N = 10 при краевых условиях заделки:

Результаты расчетов представлены на рис. 2, 3.
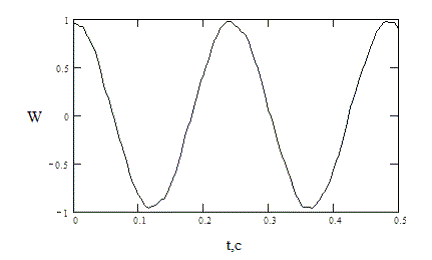
Рисунок 2 – Зависимость от времени средней точки балки.
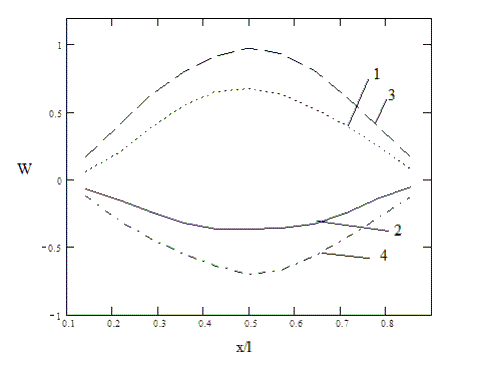
Рисунок 3 – Распределение прогиба по длине балки в разные моменты времени: 1– при
t=0,02 с, 2 – при t=0,11 с, 3 – при t=0,17 с, 4– при t=0,22 с.
Выводы
На основе уравнения Лагранжа второго рода построена математическая модель колебаний балки с переменной массой и нагрузкой. Выполнены численные расчеты в MATHCAD и получена функция прогиба балки в зависимости от времени. Объектом приложения разработанной модели является балка мостового крана, применяющаяся в колесном цехе электровагоноремонтного завода для перемещений колесной пары. Модель позволяет оценить имеющиеся наблюдения и дает адекватную оценку поведения конструкции при определенном воздействии нагрузки в заданный момент времени.