Анотація
О. Л. Сокольський, І. І. Івіцький, В. І. Сівецький, І. О. Мікульонок Визначення в’язкості пристінного шару у формуючих каналах обладнання для переробки полімерів. The research objective is definition of the processed polymeric material melt properties in a wall boundary layer of working equipment channels. Setting the slip coefficient, that provides a linear relation between the viscosity in the boundary layer and the slip coefficient which often don't correspond to reality is a standard procedure in one of the most common polymer melts flow numerical simulation software package Ansys Fluent. The experimental researches of the viscosity boundary layer slip coefficient for the three types of polyolefins have shown its non-linear, noninvariant for different polymers types, in some cases with the extreme presence. The form of this dependence varies with the flow rate increase of the polymer passes through three stages caused by the wall effect is established. The results of these researches allow more accurate considering of the boundary conditions for the polymer processing numerical modeling and optimize the accuracy of the design parameters.
Вступ
Проектування екструзійних головок, зокрема визначення геометричних параметрів каналів, по яких рухається розплав полімеру та набуває форми профілю одержуваного виробу і які безпосередньо впливають на якісні показники цього виробу, є важливим питанням у практиці перероблення полімерів і пластичних мас.
На розподіл основних параметрів розплаву в каналах екструзійних головок, а отже, і на експлуатаційні властивості виробів, значною мірою впливають пристінні ефекти. Врахування під час моделювання процесу течії реологічних властивостей рідини з пристінним шаром, що має в’язкість, відмінну від в’язкості основного шару (ядра потоку
), надасть можливість підвищити точність опису аномальних ефектів, які проявляються під час течії полімерів.
У праці [1] розглядається аналітичне розв’язання однієї з найпростіших задач розподілу швидкості в ламінарному пристінному шарі під час руху тонкої пластини великої довжини в стаціонарному незбуреному потоці в’язкого середовища. Спрямування пластини збігається з лініями течії. Передбачається, що пластина має нульову товщину, а товщина пристінного шару настільки мала, що лінії течії не змінюють свого розміщення. Проте такі спрощення надто ідеалізують задачу і зумовлюють значну похибку для реальних умов переробки полімерних матеріалів.
Також було розглянуто розрахунок пристінного шару під час течії в’язкого середовища в круглій трубі [2]. При цьому було зроблено припущення про зміну швидкості в ядрі потоку розплаву за параболічною залежністю, а в пристінному шарі — за прямою.
Одним із методів моделювання впливу пристінного шару на течію ядра потоку полімеру є введення в розрахункову схему тонкого шару матеріалу біля стінки із властивостями, відмінними від властивостей основного шару, що імітує наявність низькомолекулярних фракцій у пристінному шарі полімеру (застосування змащувальних домішок під час екструзії) [3].
Постановка задачі
Течію розплаву полімеру в пристінному шарі можна розглядати як потік між двома паралельними нескінченими стінками, одна з яких нерухома, а інша, якою є поверхня між пристінним шаром та основним потоком полімеру, рухається з постійною швидкістю. При цьому зробимо припущення, що в напрямі руху існує довільний градієнт тиску, відмінний від нуля. Такий підхід дає змогу визначити основні параметри процесу течії полімеру в каналі.
Метою дослідження є визначення властивостей розплаву перероблюваного матеріалу в пристінному шарі, зокрема — в’язкості цього розплаву.
Розв’язання задачі й аналіз отриманих результатів
Якщо для певного полімеру відомі коефіцієнти тертя по різних матеріалах, то можна розрахувати швидкості руху та в’язкість у пристінному шарі.
Залежність між напруженням зсуву на обмежувальній поверхні (твердій стінці) каналу та в’язкістю в пристінному шарі може бути описана різними законами залежно від природи полімеру та умов течії. В загальному випадку для певної температури
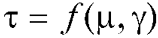 ,
,
де 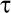 — напруження зсуву на стінці, Па;
— напруження зсуву на стінці, Па;  — в’язкість пристінного шару, Па·с;
— в’язкість пристінного шару, Па·с;  — швидкість зсуву на стінці, 1/с.
— швидкість зсуву на стінці, 1/с.
В’язкість своєю чергою є функцією швидкості зсуву, але згідно із законом Ньютона

Коефіцієнт пристінного тертя між твердою стінкою та в’язкою рідиною відповідно до [4] становить

де 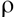 — густина в’язкої рідини в пристінному шарі, кг/м3; V — швидкість руху в’язкої рідини на межі пристінного шару та основного потоку, м/с. При цьому товщину пристінного шару можна визначити за рекомендаціями [5].
— густина в’язкої рідини в пристінному шарі, кг/м3; V — швидкість руху в’язкої рідини на межі пристінного шару та основного потоку, м/с. При цьому товщину пристінного шару можна визначити за рекомендаціями [5].
З урахуванням (1) і (2) можна отримати залежність для визначення в’язкості пристінного шару:

З формули (3) видно, що в’язкість пристінного шару прямо пропорційно залежить від коефіцієнта пристінного тертя та обернено пропорційно — від швидкості зсуву. Ця формула може бути використана для розрахунку в’язкості в пристінному шарі з урахуванням експериментально визначеного чи довідкового значення коефіцієнта пристінного тертя і разом з положеннями математичної моделі та її основними залежностями — для числового моделювання.
Отже, для застосування запропонованого методу визначення в’язкості пристінного шару потрібне знання залежності коефіцієнта пристінного тертя від температури T, яку визначають обробленням експериментальних даних.
Авторами були проведені відповідні дослідження для різних марок полімерів. Так, для поліетилену високої густини (ПЕВГ) марки 18802-020 зазначену залежність наведено на рис. 1.
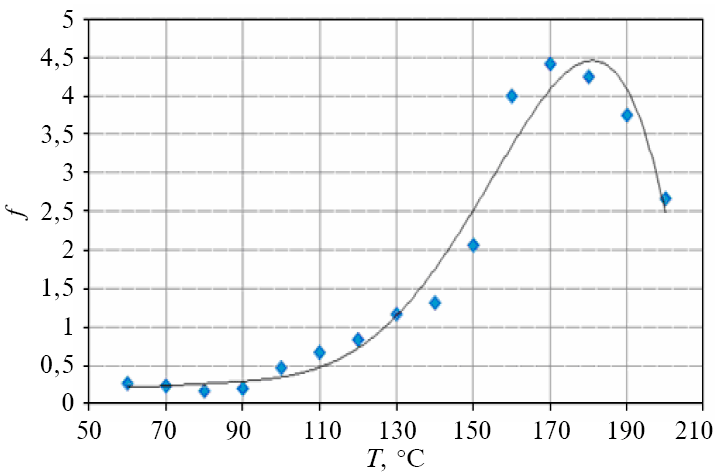
Рисунок 1 – Залежність коефіцієнта пристінного тертя від температури для ПЕВГ 18802-020
Для зручності використання в розрахунках отримані дані були апроксимовані методом найменших квадратів:
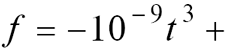

На рис. 2 наведено залежність між температурою та в’язкістю в пристінному шарі для трьох полімерів: поліетилену високої густини (ПЕВГ) марки 18802-020, поліетилену низької густини (ПЕНГ) марки 15803-020 і поліпропілену (ПП) марки 010.
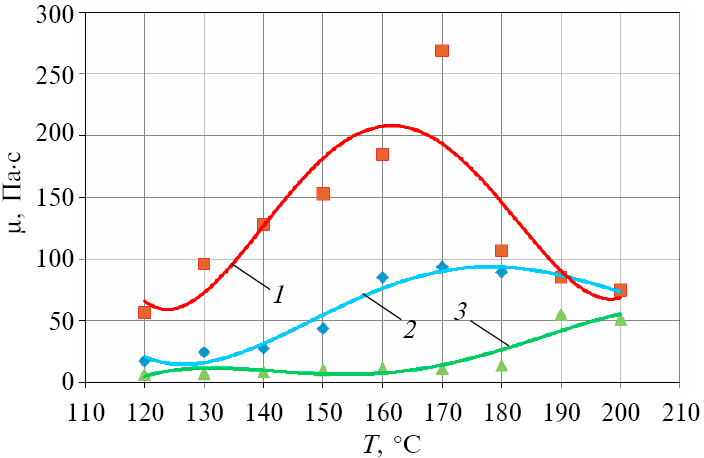
Рисунок 2 – Залежність в’язкості пристінного шару від температури:
1 — ПЕНГ; 2 — ПЕВГ; 3 — ПП
Наведені на рис. 2 залежності також апроксимовані методом найменших квадратів поліномами:
— для ПЕНГ з достовірністю R = 0,83
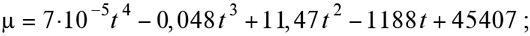
— для ПЕВГ з достовірністю R = 0,96
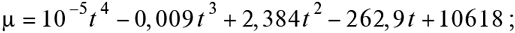
— для ПП з достовірністю R = 0,86
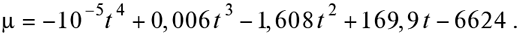
Виходячи з наведених на рис. 2 графічних залежностей, можна зробити висновок, що для кожного полімеру є певний діапазон температури, в якому пристінний шар набуває максимальної в’язкості і відбувається прилипання матеріалу до твердої стінки. Цей діапазон становить: для ПЕВГ 18802–020 – 160–165 °С, для ПЕНГ 15803–020 – 175–180 °С, для ПП 010 – 195–200 °С.
Відповідно до стандартної процедури задання коефіцієнта пристінного тертя перероблюваного полімеру в програмному комплексі Ansys Fluent [6] на рис. 3 наведена залежність між в’язкістю в пристінному шарі потоку розплаву полімеру та коефіцієнтом пристінного тертя.

Рисунок 3 – Залежність в’язкості пристінного шару розплаву полімеру від коефіцієнта пристінного тертя, задана в програмному комплексі Ansys Fluent
Із зображеного на рис. 3 графіка видно, що зазначена залежність є прямолінійною і в’язкість пристінного шару потоку розплаву полімеру не залежить від типу і марок досліджених поліолефінів, тому значення максимальної в’язкості відповідає значенню максимального коефіцієнта пристінного тертя. Але, як показали проведені експериментальні дослідження, це не відповідає дійсності й суттєво впливає на точність числового моделювання.
Авторами було проведено числове моделювання течії трьох зазначених полімерів з урахуванням наявності пристінного шару та експериментально визначеними коефіцієнтами пристінного тертя за швидкості екструзії 0,01; 0,022 і 0,037 м/c і температури 150 °C. У результаті було отримано уточнені залежності між коефіцієнтом пристінного тертя та в’язкістю в пристінному шарі (рис. 4).
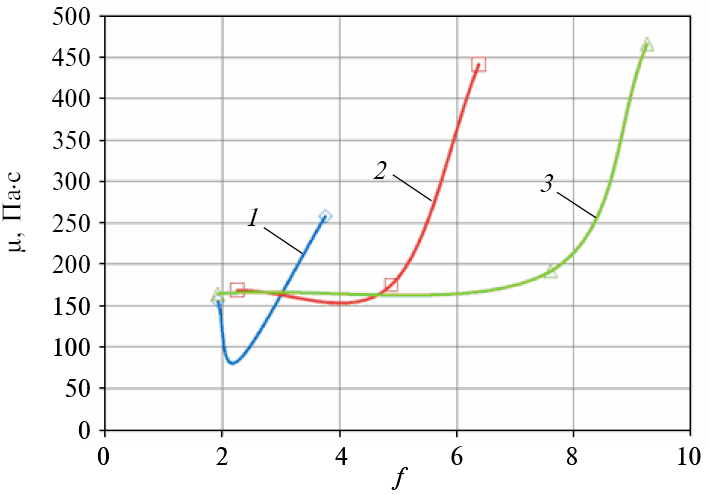
Рисунок 4 – Залежність в’язкості пристінного шару від коефіцієнта пристінного тертя:
1 — ПП; 2 — ПЕВГ; 3 — ПЕНГ
З рис. 4 можна зробити висновок, що характер залежності між коефіцієнтом тертя та в’язкістю пристінного шару для плоского щілинного каналу має нелінійний характер.
Висновки
Результати проведених експериментальних досліджень дадуть змогу виконувати уточнене числове моделювання процесу течії полімерів і пластмас у робочих органах технологічного обладнання з урахуванням пристінного тертя перероблюваного матеріалу й отримати залежності коефіцієнтів тертя від в’язкості пристінного шару та швидкості екструзії.
За результатами проведених досліджень можна зробити такі висновки.
1. За невеликих значень коефіцієнта тертя в пристінному шарі має місце лише в’язке тертя з прилипанням пристінного шару перероблюваного матеріалу до обмежувальної поверхні (твердої стінки), внаслідок чого в’язкість пристінного шару сумірна із в’язкістю ядра потоку. За подальшого збільшення коефіцієнта тертя в’язкість пристінного шару поступово зменшується (див. рис. 4).
2. Для деяких типів полімерів існують певні значення коефіцієнта тертя (у проведених дослідженнях — для поліпропілену марки ПП–010), за якого в’язкість пристінного шару внаслідок нелінійного характеру в’язкості досягає явно вираженого мінімуму.
3. За достатньо високих значень коефіцієнта тертя може виникати ефект відривання потоку матеріалу від обмежувальної поверхні каналу, що обумовлює релаксацію напружень у пристінному шарі та збільшення його в’язкості. Під час експериментальних досліджень у цьому разі спостерігався режим течії з періодичним відривом потоку перероблюваного матеріалу від поверхні каналів технологічного обладнання та його оснастки.
Напрямом подальших досліджень може бути проведення числового моделювання процесів переробки полімерів з урахуванням ефектів пристінного тертя з метою одержання виробів широкої номенклатури з різноманітних полімерних матеріалів.
Список літератури
1. Кирпиков В.А., Шорин Г.Н. Введение в теорию пограничного слоя: Учеб. пособие / Под ред. А.А. Гухмана. — М.: МИХМ, 1974. — 287 с.
2. Шиллер Г. Теория пограничного слоя. — М.: Наука, 1969. — 774 с.
3. Сівецький В.І., Сокольський О.Л., Бурла Ю.В. Дослідження процесу екструзійного формування полімерів з урахуванням ефекту пристінного ковзання // Вісник НТУУ КПИ
. Хімічна інженерія, екологія та ресурсозбереження. — 2009. — № 1. — с. 17—21.
4. Романченко П. Н. Гидродинамика и тепломассообмен в пограничном слое. — М.: Энергия, 1974. — 235 с.
5. Клаз С.И., Канавец И.Ф. Пристенные эффекты при экструзии термопластов // Пластические массы. — 1966. — № 3. — С. 47—50.
6. ANSYS Fluent Features [Online]. Avaliable: http://www.ansys.com/