Анотація
Л.Г. Воронін, М.П. Швед, Д.М. Швед, І.В. Луценко Дослідження процесу плавлення полімеру при черв’ячній екструзії. У статті досліджується процес плавлення в каналі одночерв’ячного екструдера з метою зменшення енергоємності процесу та підвищення ефективності плавлення полімеру. Проведено аналіз основних підходів для отримання кількісного результату процесу дисперсійного плавлення гранульованого полімеру при черв’ячній екструзії. Отримана залежність розподілу температури по радіусу диспергованої сферичної частини полімеру Ключові слова: черв’ячна екструзія, плавлення, полімер, дисперсійна модель плавлення, гранула.
1. Вступ
Процесам переробки полімерів приділяється значна увага, оскільки з року в рік зростає питома вага виробів із полімерів. Зростаючі обсяги виробництва та переробки полімерних матеріалів вимагають від галузі полімерного машинобудування оптимізації процесу та ширшого використання ресурсоенергозберігаючих технологій.
Найбільш поширеною залишається одночерв’ячна екструзія. При цьому одночасно виконуються наступні операції: живлення, стискання, плавлення твердого полімеру, змішування, створення тиску та дозування розплаву.
Всі названі процеси тісно пов’язані між собою і виконуються в черв’ячному екструдері одним робочим органом - черв’яком, що ускладнює оптимізацію процесів [1, 2, 4].
Метою роботи є підвищення ефективності плавлення в каналі черв’ячного екструдера, що дасть змогу зменшити енергоємність процесу екструзії.
2. Аналіз літературних даних і постановка проблеми
В дослідженнях процесу плавлення полімеру в каналі черв’ячного екструдера використовують різні фізичні та математичні моделі, які відрізняються трактуванням процесу, врахуванням різних чинників і точністю процесу.
Вперше процес плавлення в одночерв’ячних екструдерах описаний Маддоком [4-6]. Тип плавлення, який досліджувався Маддоком відносився до моделі плавлення безперервного шару твердої фази. В середині 1980-х років Тадмором було проведено експериментальну роботу та теоретичний аналіз з розробкою класичної математичної моделі плавлення.
В цій, так званій «пробковій» моделі процес плавлення розглядається в декартовій системі координат. Умовою руху матеріалу в зоні плавлення є більше тертя між пробкою й циліндром, аніж тертя між пробкою і черв’яком. Унаслідок тертя й передачі теплової енергії від поверхні стінки циліндра утворюється тонка плівка розплаву. Поступово плівка стовщується і, коли вона стає більшою, аніж радіальний зазор між циліндром і гребенем черв’яка, останній починає зіскрібати шар розплаву, який збирається біля його штовхаючої поверхні. Із просуванням пробки гранул уздовж каналу її ширина зменшується, а плавлення закінчується, коли пробка зникає.
Таку модель побудовано на припущенні, що рух матеріалу в зоні плавлення є стаціонарним, поля швидкостей і температур у кожному перерізі каналу є сталими, а полімер має чітко виражену температуру плавлення. Подальші спрощення полягали в тому, що пробку вважали гомогенною, однорідною й безперервною, а поперечний переріз області розплаву й пробки – прямокутним. Теплота до твердої пробки передається від внутрішньої поверхні циліндра крізь тонку плівку розплаву, що рухається над пробкою. Додаткова теплота генерується в плівці внаслідок роботи в’язкого тертя [2, 3].
Теплопередачею в напрямку вісі циліндра та від штовхаючої стінки гребня черв’яка до шару розплаву нехтують, оскільки на більшій частині зони плавлення ширина твердої пробки набагато перевищує її висоту. Товщину шару гранул в пробці вважають значною, і, оскільки коефіцієнт теплопровідності гранул є малим, температура гранул, що контактують з плівкою, швидко знижується від температури розплаву до температури шарів пробки, досить віддалених від зони контакту. Швидкість плавлення в тонкому шарі на поверхні розділу розплав – пробка
в будь-якому поперечному перерізі визначається потужністю теплового потоку, що підводиться до поверхні плавлення [7, 8].
Як було зазначено, плавлення безперервного шару твердої фази представляє собою найбільш поширену методику підходу при моделюванні процесу екструзії. Проте в деяких дослідженнях було встановлено, що тверді частинки за певних умов насправді не стикаються, а є диспергованими в розплавленому матеріалі. Найяскравішими прикладами є екструдери з циліндрами, які оснащені канавками, двошнекові екструдери, або такі, де передбачено повернення частини розплаву в зону плавлення. Дисперсійна модель плавлення зображена на рис. 1.
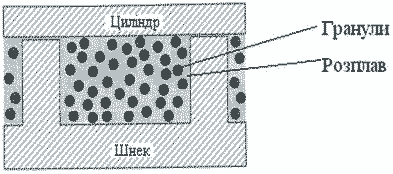
Рисунок 1 – Дисперсійна модель плавлення полімеру
Попередньо проведені дослідження показали, що довжина зони плавлення при застосуванні дисперсійної моделі значно зменшується і складає 3-5D проти 10-15D по моделі Тадмора.
З метою інтенсифікації процесу та зменшення загальної довжини зони плавлення запропоновано реалізувати модель дисперсійного плавлення при одночерв’ячній екструзії.
Найчастіше для цього розроблюються спеціальні конструкції черв’яків прикладами яких є багатозахідні шнеки і шнеки для високих тисків [9].
Автори вважають, що дисперсійної моделі плавлення в черв’ячному екструдері можна досягти без зміни конструкції головного органу, а за допомогою голодного
живлення, тобто при обмеженій подачі матеріалу в зону завантаження. Дисперсійна модель плавлення з обмеженою подачею представлено на рис. 2.
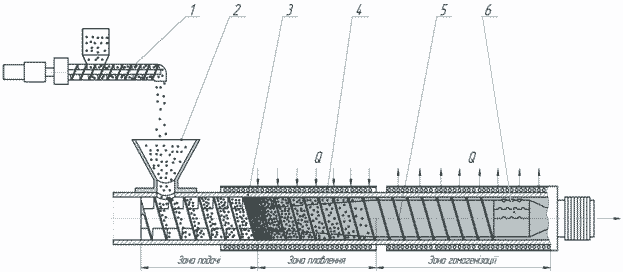
Рисунок 2 – Дисперсійна модель плавлення з обмеженою подачею:
1-дозатор, 2-завантажувальна воронка, 3-циліндр, 4-нагрівник, 5-черв’як, 6-змішуючий елемент
3. Математична модель процесу
У дисперсійній моделі плавлення приймається, що частинки однорідні, мають сферичну форму і дисперговані в розплавленому полімері. Для заповнення простору між твердими частинками необхідно деякий мінімальний об’єм розплаву. Це означає, що дана модель може бути застосована після того, як деяка кількість твердого матеріалу вже розплавлена, або частина розплаву після зони гомогенізації повертається в зону плавлення [2].
Приймається, що нагрівання твердих частинок відбувається шляхом теплопровідності рівномірно, і незалежно від місцезнаходження частинки у каналі. Теплота, що витрачається на нагрівання частинок визначається сумою теплоти, яка підводиться через канал (через циліндр і черв’як) і теплотою в’язкого тертя, що генерується в розплаві полімеру [10].
Однією з головних задач дисперсійної моделі плавлення є визначення тривалості плавлення і довжини каналу зони плавлення. При кожному значенні часу визначається розподіл температур по радіусу частинки, яка знаходиться у розплаві. Розрахунок закінчується, коли в центрі гранули температура досягає температури плавлення.
Зміна температури всередині гранули може бути представлено законом теплопровідності (Закон Фур’є):

де 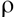 - густина полімеру, Cp - питома теплоємність,
- густина полімеру, Cp - питома теплоємність, 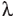 - теплопровідність, які є функціями від температури.
- теплопровідність, які є функціями від температури.  - оператор Лапласа, який в сферичних координатах має вигляд:
- оператор Лапласа, який в сферичних координатах має вигляд:
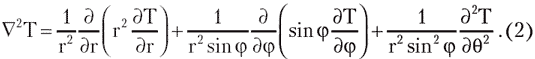
Якщо прийняти, що температура по координаті  та Q не змінюється, то рівняння теплопровідності (1) в сферичних координатах приймає вигляд:
та Q не змінюється, то рівняння теплопровідності (1) в сферичних координатах приймає вигляд:

Після перетворення рівняння теплопровідності (3) з граничними умовами записується:

де T0 - початкова температура, Tp - температура розплаву, r - поточний радіус, який змінюється від r = 0 в центрі сферичної гранули до r = R на її поверхні, 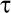 - поточний час.
- поточний час.
Крайова задача (4), (5) не має аналітичного розв’язку, тому що 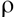 , Cp та
, Cp та 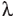 є функціями температури, і може бути розв’язана методом сіток. Запишемо ці рівняння в скінченних різницях:
є функціями температури, і може бути розв’язана методом сіток. Запишемо ці рівняння в скінченних різницях:

де 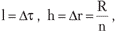 індекси i та j-зміна по температурі та по радіусу відповідно.
індекси i та j-зміна по температурі та по радіусу відповідно.
Метод сіток дозволяє визначити температурне поле в середині гранули. Коли температура в центрі гранули досягає температури плавлення процес закінчується. Час, який відповідає тривалості досягнення необхідної температури, і є часом плавлення. На рис. 3 представлено графік залежності температури в центрі гранули в залежності від часу перебування її в розплаві.
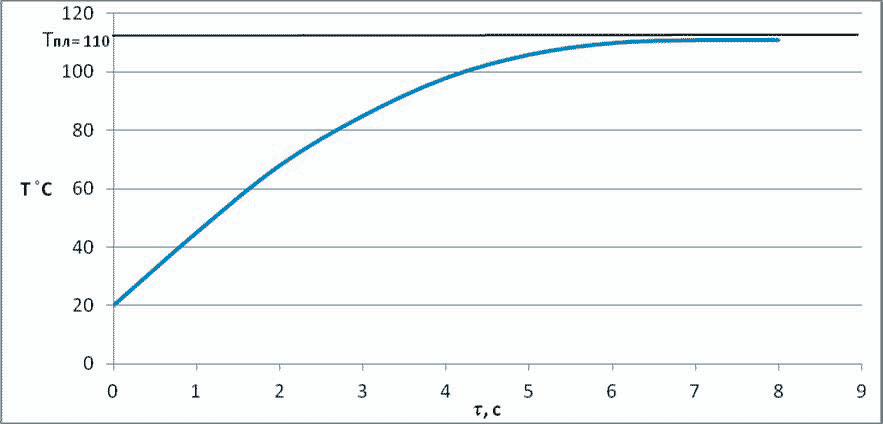
Рисунок 3 – Графік залежності розподілу температури Т в центрі сферичної гранули діаметром 5 мм для поліетилену високого тиску марки 15803-020 в залежності від часу  її перебування в розплаві
її перебування в розплаві
4. Висновки
У даній роботі проведено аналіз основних математичних моделей для отримання кількісного результату процесу плавлення при черв’ячній екструзії. Запропоновано та обґрунтовано використання дисперсійної моделі.
Наведено порядок розрахунку для отримання залежності розподілу температур диспергованої сферичної частинки полімеру по її радіусу.
Попередньо проведені експериментальні дослідження показали, що вищенаведений алгоритм дозволяє розраховувати час перебування гранули в зоні плавлення, а відповідно і довжину гвинтової нарізки в цій зоні в залежності від продуктивності.
Література
1. Раувендааль, К. Экструзия полимеров [Текст]: пер. с англ. – А. Я. Малкина – СПб.: Профессия, 2006. – 768 с.
2. Тадмор, З. Теоретические основы переработки полимеров [Текст] / З. Тадмор, К. Гогос. – М.: Химия, – 1984. – 632 с.
3. Раувендаль, К. Выявление и устранение проблем в экструзии [Текст]: пер. с англ. – В. П. Володина – СПб.: Профессия, 2008. – 328 с..
4. Радченко, Л.Б. Переробка термопластів методом екструзії [Текст] / Л. Б. Радченко. — К. : ІЗМН, 1999. — 220 с.
5. Nichols, R. Modern Plastics [Текст] / R. Nichols, F. Kheradi // Int. Polym. Process. – 1984 – T 1 (1). – c. 15-31.
6. Griffith, R. Fully Developed Flow in Screw Extruders [Текст] / R. Griffith // Ind. Eng. Chem. Fundam. –1962 – T. 27 (3). – c. 180— 187.
7. Tadmor, Z. Engineering Principles of Plasticating Extrusion [Текст] / Z. Tadmor, T.Klein // van Nostrand Romhold comp. – 1970 – T. 51 (6). – c. 46-54.
8. Tadmor, Z. Solids Conveying in Screw Extruders. Part I. A Modified Isothermal Model [Текст] / Z. Tadmor, E. Broyer // Polym. Eng. Sci. – 1972 – T. 117(12). – c. 12-24.
9. Tadmor Z. Solids Conveying in Screw Extruders. Part II. Non Isothermal Model [Текст] / Z. Tadmor, E. Broyer // Polym. Eng. Sci. – 1972 – T. 117(12). – c. 378-386.
10. Donovan, R. A Theoretical Melting Model for Plasticating Extruders [Текст] / R. Donovan // Polym. Eng. Sci. – 1971 – T. 100- (11). – c. 247-257.