Аннотация
С.И. Завинский Теоретический подход к описанию процесса экструзии композитного органического сырья. Рассмотрен вопрос формирования теоретического подхода к описанию движения композитного органического сырья в предматричной зоне экструдера. В качестве основы для этого принято описание движения жидкости в коаксиальном конфузоре, которое необходимо дополнить сведениями о реологических характеристиках сырья с учетом тепловых эффектов.
Ключевые слова: композитное органическое сырье, предматричная зона, коаксиальный конфузор, одношнековый экструдер.
1. Введение
Проектирование оптимальных конструкций аппаратов химической промышленности — одна из наиболее актуальных задач, от решения которой в значительной степени зависит эффективность технологических процессов. Основные принципы проектирования и расчета элементов такого оборудования изложены в ряде научных работ последних лет. Например, в работах [1-4] подробно исследованы роторные аппараты и процессы мокрого улавливания пыли в аппаратах такого типа, а также эффективность этих процессов в зависимости от конструктивных параметров. Шнековые экструдеры в силу своей предназначенности для переработки органического сырья также могут быть отнесены к аппаратам химической промышленности и, соответственно, должны исследоваться на предмет возможной оптимизации их конструкций с целью повышения эффективности
реализуемых в них технологических процессов. Применение шнековых экструдеров для переработки композитного органического сырья становится все более актуальным вопросом в химической промышленности. Актуальность исследования экструдеров подтверждает большое количество публикаций и патентов, многие из которых направлены на аспекты практического применения экструдеров и на процессы преобразования материала в экструдере.
В настоящее время экструдеры применяются не только в традиционных технологиях переработки полимеров, но и все шире в технологиях получения композитных материалов или переработки композитного органического сырья. В качестве примеров можно привести древесно-полимерные композитные материалы (ДПК), топливные брикеты [5-7], экструдированные комбикорма [8] и пищевые продукты, биоразлагаемые полимерные изделия, органо-минеральные удобрения с контролируемым высвобождением питательных компонентов.
В указанных технологиях распространены одно- и двухшнековые экструдеры. Двухшнековые экструдеры обладают более широкими технологическими возможностями [9] при организации различных функциональных зон по длине шнекового канала с различной температурой и давлением, подводом и отводом продуктов химических реакций, тепла, с различным градиентом сдвига и т. д., имеют более широкие возможности автоматизации и регулирования. В то же время одношнековые экструдеры имеют более простую конструкцию, и большую производительность, а также позволяют получить более высокую удельную энергонапряженность процессов, особенно в предматричной зоне.
Анализ конструкции одношнекового экструдера, имеющего различные функциональные зоны (транспортную, нагрева, гомогенизации, сжатия, уплотнения, разуплотнения и т. д.) [10], показывает, что наиболее глубокие изменения структуры материала происходят в предматричной зоне, где обычно наблюдаются самые высокие температуры, давления, и градиенты сдвига.
В предматричной зоне экструдера материал, как правило, переходит в вязко-пластичное состояние и его движение, можно рассматривать как ползущее течение неньютоновской жидкости в соосном коническом конфузоре, образованном поверхностью матрицы и корпусом шнека.
Целью настоящей работы является формирование теоретического подхода к исследованию предматричной зоны экструдера при переработке композитного органического сырья.
Основными задачами для достижения поставленной цели являются: обзор известных работ, математическая формулировка задачи, анализ полученного решения и постановка задач дальнейшего теоретического исследования.
2. Обзор ранних работ
Систематического исследования ползущего течения в соосных конических конфузорах до настоящего времени не было. В работе [11] предлагается использовать для расчета течений в любых соосных кольцевых каналах переменного сечения ступенчатую аппроксимацию отрезками кольцевых прямолинейных труб. Данное предложение можно отнести и к соосным коническим конфузорам, хотя данная методика авторами работ предлагалась для диффузорного течения, но при таком подходе сходящиеся течения заменяются прямолинейными, что может привести к значительным погрешностям, особенно в случае больших значений углов раскрытия граничных поверхностей.
В работе [12] приведено выражение для расчета перепада давления в сужающемся зазоре межу двумя коническими поверхностями, но без объяснения входящих в него параметров. Автором в работе [13] сделан краткий анализ распределения скорости и давления в соосном коническом конфузоре с общей вершиной границ.
3. Математическая формулировка задачи
Наиболее системными и исчерпывающими являются постановка и решение задачи о ползущем течении в соосном коническом конфузоре с общей вершиной границ, приведенная в [14].
Были приняты следующие обозначения (рис. 1):
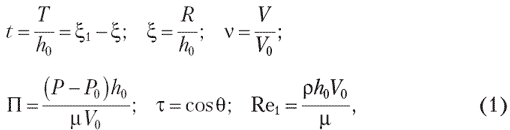
где h0 — линейный масштабный множитель, использующийся для обезразмеривания переменных в уравнениях движения жидкости, в дальнейшем величина h0 будет идентифицирована как ширина канала на выходе;
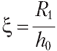 — безразмерная координата входа в канал;
— безразмерная координата входа в канал;
V0 — средняя по площади поверхности поперечного сечения входа в канал скорость жидкости, которая определяется выражением:

где S1 — площадь поперечного сечения канала координатной поверхностью на его входе:

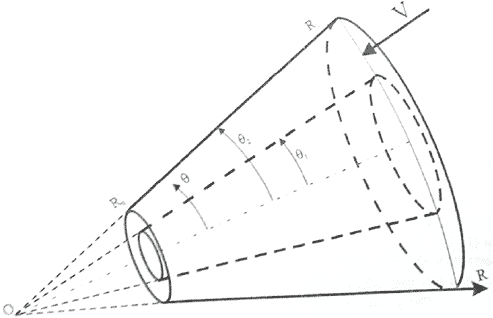
Рисунок 1 — Геометрия соосного конического конфузора с общей вершиной границ:
О — вершина границ, она же полюс сферической системы координат;
R — радиальная сферичесая координата;
R0 — радиальная координата выхода из конфузора;
R1 — радиальная координата входа в конфузор;
V — скорость жидкости; 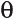 — азимутальная сферическая поверхность;
— азимутальная сферическая поверхность;
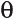 1,
1, 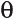 2 полууглы раскрытия внутренней и внешней границ канала
2 полууглы раскрытия внутренней и внешней границ канала
В результате получено аналитическое решение вида:
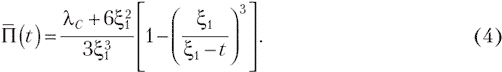
Данное решение позволяет определить одну из основных характеристик течения в предматричной зоне — гидравлические потери, преодоление которых происходит за счет шнекового нагнетателя. Следовательно мы получили исходные данные для его расчета.
Описание движения реального композитного сырья осложняется существенным влиянием температуры и градиента сдвига на вязкость жидкости. Поэтому уравнение (4) необходимо дополнить сведениями о реологических характеристиках сырья, а также уравнением теплового баланса.
Кроме того, градиент сдвига внутри потока при движении сырья в предматричной зоне возникает не только при его движении между поверхностью матрицы и корпуса шнека, но и за счет относительного движения (поворота) корпуса шнека и матрицы. Возникающий при этом сдвиг существенно изменит эффективную вязкость сырья, а значит и распределение давлений в предматричной зоне.
Граничные условия потока на стенках матрицы и корпуса шнека в реальности могут отличаться от принятых нами условий прилипания
потока к стенкам, и в то же время искусственно создавая условия для сцепления сырья и границ потока, можно влиять на градиент сдвига внутри потока и опять же на распределение давлений в предматричной зоне.
4. Выводы
В рамках принятого теоретического подхода дальнейшие теоретические и практические исследования должны иметь следующие направления:
- определение реологических характеристик конкретных видов сырья, подлежащего переработке в экструдере;
- определение граничных условий, реально имеющихся в потоке в предматричной зоне и разработка конструктивных мероприятий, обеспечивающих целенаправленное управление ими;
- провести учет тепловых эффектов при движении композитного органического сырья в предматричной зоне.
Литература
1. Питак, И. В. Основы теории и расчета деталей роторного аппарата [Текст] / И. В. Питак // Восточно-Европейский журнал передовых технологий. — 2012. — № 4/7(58). — с. 14—17.
2. Питак, И. В. Определение основных параметров роторного аппарата [Текст] / И. В. Питак, В. Ф. Моисеев, П. В. Кузнєцов // Вестник Национального технического университета ХПИ
.—2012. — № 39. — с. 60—68.
3. Питак, И. В. Исследование процесса мокрого улавливания пыли в роторном вихревом аппарате [Текст] / И. В. Питак // Вестник Национального технического университета ХПИ
. — 2010. — № 17. — с. 135—140.
4. Питак, И. В. Положительные аспекты работы роторного вихревого аппарата на промышленных предприятиях [Текст] / И. В. Питак, В. Ф. Моисеев // Вестник Национального технического университета ХПИ
. — 2009. — № 15. — с. 9—13.
5. Трошин, А. Г. Развитие процессов и оборудование для производства топливных брикетов из биомассы [Текст] / А. Г. Трошин, В. Ф. Моисеев, И. А. Тельнов, С. И. Завинский // Восточно-Европейский журнал передовых технологий. — 2010. — № 3/8(45). — с. 36—40.
6. Тельнов, И. А Исследование кинетики сушки опилок и сружки в интенсивном режиме [Текст] / И. А. Тельнов, С. И. Завинский, А. Г. Трошин, В. Ф. Моисеев // Вестник НТУ ХПИ
. — 2012. — № 10. — с. 139—144.
7. Завинский, С. И. Влияние давления прессования и температуры на свойства брикетов из древесной стружки [Текст] / С. И. Завинский, И. А. Тельнов, А. Г. Трошин, В. Ф. Моисеев // Вестник НТУ ХПИ
. — 2012. — № 10. — с. 144—149.
8. Афанасьев, В. А. Научно-практические основы тепловой обработки зерновых компонентов в технологии комбикормов [Текст] : дис. / В. А. Афанасьев. — Москва, 2003. — 517 с.
9. Kohlgr ber, K. Der gleichl ufige Doppelschnecken-extruder [Text] / K. Kohlgr ber. — M nchen, 2007. — 373 p.
10. Завинский, С. И. Исследование предматричной зоны в процессе экструдирования композитного органического сырья [Текст] / С. И. Завинский, И. А. Тельнов, А. Г. Трошин // ХХI международная научно-практическая конференция, Ч. III Інформаційні технології
. — Харьков, 2013. — с. 16.
11. Хан, Ч. Д. Реология в процессах переработки полимеров [Текст] / Ч. Д. Хан. — М.: Химия, 1979. — 368 с.
12. Рогов, Б. В. Уравнения вязких течений в гладких каналах переменного сечения [Текст] / Б. В. Рогов, И. А. Соколова // Доклады РАН. — 1995. — Т. 345, № 5. — с. 615—618.
13. Панов, А. К. Гидродинамика потоков аномально-вязких нелинейных систем в формующих каналах [Текст] / А. К. Панов, А. Р. Анасов. — Уфа : Гос. нефт. техн. ун-т, 1994. — 258 с.
14. Ульев, Л. М. Ламинарные течения в соосных конических каналах [Текст] : монография / Л. М. Ульев. — Т. 1. — Х.: НТУ ХПИ
, 2006. — 660 с.