Истощение мировых запасов топливных материалов вызывает стабильный интерес к возобновляемым источникам энергии – источникам на основе постоянно существующих или периодически возникающих в окружающей среде потоков энергии. Наибольших результатов в преобразовании этих потоков для промышленных нужд достигла ветроэнергетика: современные ветроустановки производят электроэнергию, соизмеримую с традиционными типами электростанций, причем доля альтернативных источников в общем производстве электроэнергии ежегодно возрастает [1].
Существует большое разнообразие конструкций ветроэнергетических установок (ВЭУ) [2]. Для Российской Федерации, территория которой является в основном равнинной, пригодны ВЭУ, способные работать в условиях относительно невысоких скоростей воздушного потока. Этому требованию отвечают ветроэнергетические установки колебательного типа (ВЭУ КТ) [3]. В данной статье исследуется одна из подобных конструкций, а также синтезируется система оптимального управления ею с целью повышения энергоотдачи.
На рис. 1 приведена кинематическая схема ВЭУ КТ [2]. Данная установка работает следующим образом: платформа 10 за счет флюгера 5 разворачивается таким образом, что опорные рамы 1 и 3 устанавливаются в положение, перпендикулярное вектору воздушного потока.
При достижении опорными рамами определенного положения поворотные лопатки переключаются в противоположное состояние. Движение боковых балок замедляется вплоть до полной остановки, затем они начинают двигаться в обратном направлении, и все действия повторяются.

Таким образом, элементы конструкции 4 и 11 совместно c поперечными тягами 9 совершают колебательные движения.
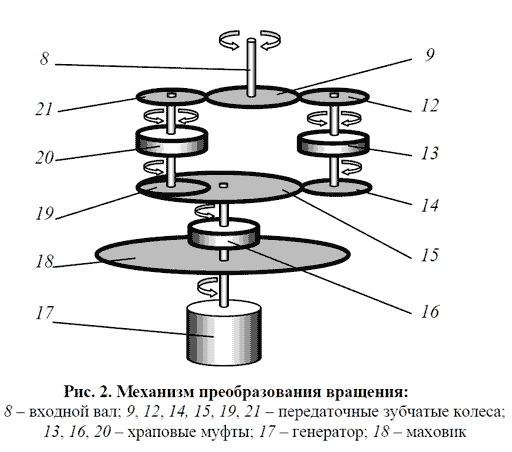
С помощью вала 8 эти колебания передаются устройству отбора мощности 7, основу которого представляет электрический генератор. Для обеспечения возможности применения стандартных электрогенераторов колебательные движения ветроустановки необходимо преобразовать в однонаправленное вращение. На рис. 2 приведен вариант конструкции такого механизма.
Входной вал 8 воспринимает колебательные движения от ветроустановки и с помощью зубчатых колес 9, 12 и 21 передает двунаправленное вращение храповым муфтам 13 и 20. Направление зацепления этих муфт различное. Благодаря этому вращение зубчатых колес 14 и 19 однонаправленное, но противоположное друг другу.
Зубчатое колесо 15 также вращается в одном направлении и получает энергию в течение всего периода колебания ВЭУ за счет внутреннего зацепления с колесом 19 и внешнего – с колесом 14. Однонаправленное вращение колеса 15 передается через храповую муфту 16 и маховик 18 ротору генератора 17, вырабатывающему электроэнергию.
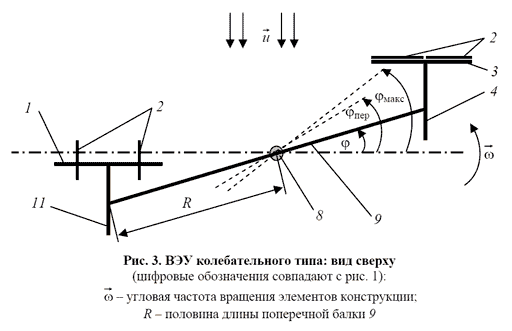
Рассмотрим рис. 3, представляющий собой вид сверху на ветроустановку.
Для построения математической модели ВЭУ КТ условно разделим всю конструкцию на две части. Одну из них, объединяющую маховик 18 и электрогенератор 17 (см. рис. 2), будем считать нагрузкой. Другую, состоящую из элементов 1-6, 8-15, 19-21, назовем собственно ветроустановкой. Соединение этих частей производится с помощью храповой муфты 16. Таким образом, конструкция является системой с переменной структурой.
По результатам расчетов построены графики изменений коэффициента сцепления μ, угла отклонения продольной балки 9 от среднего положения – φ (см. рис. 3), угловых скоростей вращения этой балки ωВЭУ и маховика ωнагр. Они изображены на рис. 4.
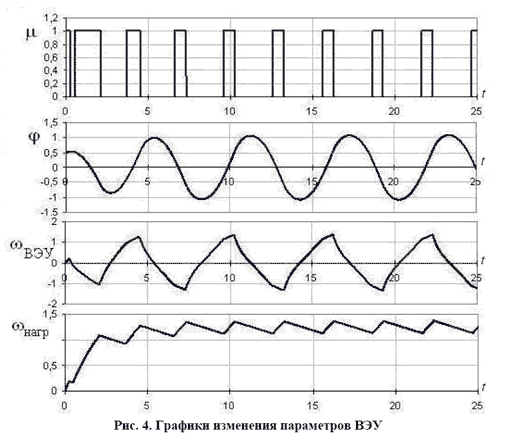
Эти графики демонстрируют следующее: в течение 5…10 с ветроустановка колебательного типа работает в режиме разгона: φ, ωВЭУ и ωнагр постепенно увеличиваются до значений, соответствующих установившемуся режиму. Изменение коэффициента сцепления μ в течение этого времени также происходит с непостоянным периодом. Управление параметрами ВЭУ в течение указанного времени нецелесообразно.
Список использованной литературы
1. Бундас В. В. Расчеты при проектировании электроснабжения. Таблицы и графики / В. В. Бундас. – М. ; Л. : Госэнергоиздат, 1961. – C. 155.
2. Ветроэнергетика : пер. с англ. / под ред. Д. де Рензо. – М. : Энергоатомиздат, 1982. – C. 271.
3. Гловацкая А. П. Методы и алгоритмы вычислительной математики / А. П. Гловацкая. – М. : Радио и связь, 1999. – C. 408.