Аннотация
Турупалов В. В., Чернышев М. М., Прядко Г. А. Математическое описание процесса теплообмена в протиточних теплообменных аппаратах. Представлены общие сведения о процессах теплообмена в теплообменных аппаратах. В качестве модели потока принята модель идеального перемешивания. Получена математическая модель теплообменника типа “перемешивание-перемешивание ” и соответствующие ей переходные процессы.
Введение
Теплообменными аппаратами называют устройства, предназначенные для передачи тепла от одного теплоносителя к другому, а также осуществления различных технологических процессов: нагревание, охлаждения, кипения, конденсации и др. В промышленности в основном используются рекуперативные теплообменники. В аппаратах этого типа горячий и холодный теплоносители подаются в разделенные глухой стенкой объемы. Теплообмен происходит через разделяющую объемы поверхность. Теплообменные аппараты являются наиболее распространенными и необходимыми элементами технологических и энергетических установок разного типа на различных предприятиях. Поэтому часто возникает необходимость исследования режимов работы теплообменных аппаратов [1,2,3].
Постановка задачи.
Для анализа работы теплообменного аппарата необходимо получить математическую модель, которая была адекватна исследуемым процессам. В процессе проектирования и работы теплообменного аппарата очень важно проанализировать [1,3]:
• установившийся (стационарный) режим работы;
• переходный процесс, возникающий в результате возмущений на входе и определить время выхода аппарата в стационарный режим работы.
Перечисленные задачи исследования работы теплообменных аппаратов можно успешно решить при использовании метода математического моделирования на основе статической или динамической моделей.
Получение математической модели.
Из множества математических методов моделирования объектов управления для реализации оперативного управления наибольший интерес представляют теоретические методы, базирующиеся на математических описаниях механизмов протекающих процессов. Таковые модели обладают хорошими прогностическими возможностями в широких диапазонах изменения свойств объектов и режимных параметров технологических процессов. Недостатки же состоят в том, что, как правило, эти модели в процессе реализации представляют недостаточно точные результаты, тем не менее, в ряде случаев, удается достичь требуемой точности. При описании процессов тепло- и массопереноса возможны идентификация и регулярная корректировка коэффициентов входящих в уравнения математической модели путем решения обратных задач переноса на базе контрольных значений промежуточных параметров технологического процесса.
Математическое описание процесса в теплообменных аппаратах удобно записать в виде выражения, которое характеризует изменение температуры в потоке теплоносителя во времени, обусловленное, во-первых, движением потока и, во-вторых, теплопередачей [3,4,5].
Если структура потока теплоносителя соответствует модели идеального перемешивания, то для математического описания этого потока можно использовать уравнение:
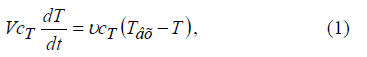
с учетом источника тепла, возникающего в потоке за счет теплопередачи:
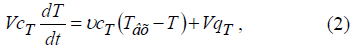
где VqT = FKTΔT - интенсивность теплообмена в реакционном объеме V;

Рисунок 1 – Схематическое изображение теплообменника типа перемешивание-перемешивание.
Для теплообменного аппарата, в котором структура потоков соответствует моделям идеального перемешивания, математическая модель представляет собой систему двух уравнений типа (3), записанных для первичного и вторичного теплоносителей:
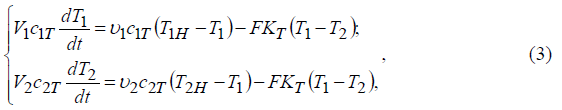
где Т1 - Т2 = ΔT, при этом Т1 и T2 имеют постоянные значения в каждой точке объемов идеального перемешивания соответственно V1 и V2: Т1H, Т2H - начальные температуры первичного и вторичного теплоносителей; Т1k = T1 и T2k= Т2 - конечные температуры первичного и вторичного теплоносителей.
Величина FKT (T1 - T2) имеет знак минус
в уравнении описания потока теплоносителя, который отдает тепло, и знак плюс
, если тепло воспринимается теплоносителем.
При выполнении условия (1) можно с достаточной для практических расчетов точностью производить линеаризацию кривых изменения температур рабочих сред. При этом изменение температуры по длине аппарата представляется линейным законом, а средняя температура первичного и вторичного теплоносителей определяется как средняя арифметическая величина [4,5,6]:

Средняя разность температур (движущая сила теплообмена) выражается равенством:
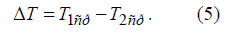
В данном случае вследствие линеаризации кривой изменения температур по длине аппарата параметры T1, T2, TNO, ΔT будут изменяться только во времени (координата длины исключается), и математическая модель может быть записана в виде обыкновенных дифференциальных уравнений.
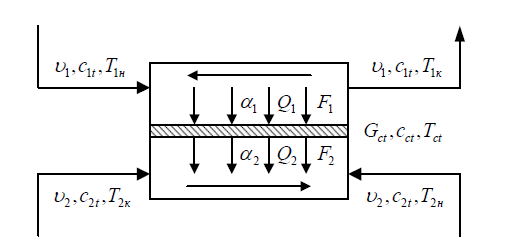
Рисунок 2 – Схема потоков в противоточном теплообменнике.
На схеме введены следующие обозначения: Q1 и Q2 - количества тепла, передаваемые через поверхность теплообмена F1 и f2; a1 a2 и a2 - коэффициенты теплоотдачи соответственно со стороны первичного и вторичного теплоносителей; GCT, cCT, TCT - вес, теплоемкость и температура стенки (принимаем, что T1CT и T2CT близки вследствие малой толщины стенки, и при составлении уравнений используем TCT вместо T1CT и Т2CT).
Математическая модель исследуемого теплообменника должна включать:
• уравнения теплового баланса:
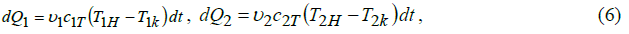
•уравнения теплоотдачи:
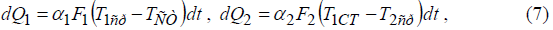
•уравнение переходного режима (динамическая характеристика):

Уравнение (8) показывает, что при теплообмене в неустановившемся потоке, когда dQ1 ≠ dQ2 , часть тепла аккумулируется стенкой в любой момент времени переходного режима.
При выборе технологии следует руководствоваться следующими факторами [3]:
Если использовать равенства (2), (3), то уравнения (4) – (8) образуют следующую систему:
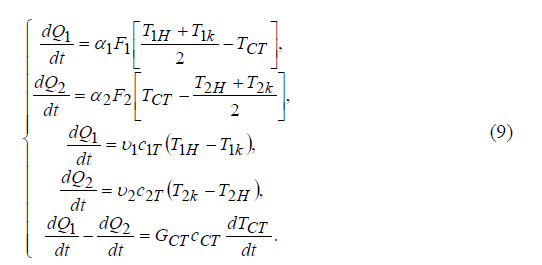
Система уравнений (9) является математическим описанием процесса теплообмена через стенку в противоточных теплообменных аппаратах, для которых можно принять допущение о линейном изменении температуры рабочих сред по длине аппарата.
Решение системы (9) нетрудно найти на ЭВМ, если привести ее к виду, удобному для моделирования:

Составим схему решения уравнения (10) в пакете Matalb&Simulink [7] представленную на рис. 3.

Рисунок 3 –Схема моделирования противоточного теплообменного аппарата в пакете Simulink

Рисунок 3 – Схема моделирования противоточного теплообменного аппарата в пакете Simulink.
В результате изменения температуры теплоносителя на входе в аппарат получены следующие переходные процессы.
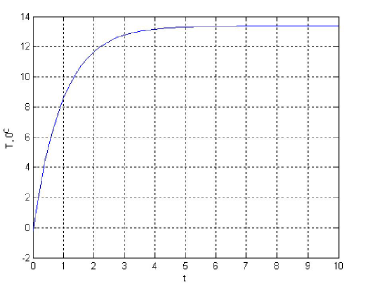
Рисунок 4 – Переходной процесс температуры T1k на выходе теплообменника.

Рисунок 5 – Переходной процесс температуры T2k на выходе теплообменника.

Рисунок 6 – Переходной процесс теплоты Q1 через поверхность теплообмена F1.

Рисунок 7 – Переходной процесс теплоты Q2 через поверхность теплообмена F2.
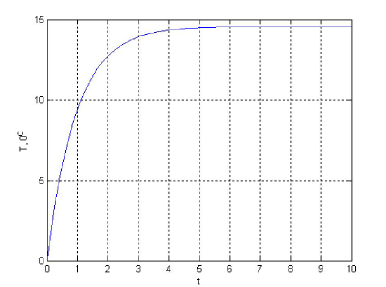
Рисунок 8 – Переходной процесс температуры стенки.
Выводы
- Получена система уравнений, которая является математическим описанием процесса теплообмена через стенку в противоточных теплообменных аппаратах с учетом линеаризации кривой изменения температур рабочих сред по длине теплообменников.
- Составлена схема моделирования динамических режимов теплообменного аппарата в пакете Matalb&Simulink.
- Получены графики переходных процессов выходных потоков теплообменногоаппарата, а так же температуры стенки и величины тепловых потоков от теплоносителя к охлаждающему потоку.
- Анализ результатов моделирования подтверждает соответствие качественного поведения модели основным характеристикам изучаемого технологического процесса.
Список использованной литературы
1. Лесохин Е. И., Рашковский П. В. Теплообменники конденсаторы в процессах химической технологии: Моделирование, расчет, управление. – Л.: Химия, 1900. – 288 С.
2. Липатов Л. Н. Типовые процессы химической технологии как объекты управления. – М.: Химия, 1973. – 320 С.
3. Шински Ф. Системы автоматического регулирования химико-технологических процессов. под ред. И. И. Гельперина. – М.: Химия, 1974. – 336 С.
4. Безденежных А. А. Моделирование химико-технологических процессов: Гидродинамические, тепло- и массообменные процессы. – Л.: ЛТИ, 1980. – 77 С.
5. Закгейм А. Ю. Введение в моделирование химико-технологических процессов. Математическое описание процессов. – М.: Химия, 1973. – 224 С.
6. Теплотехника: Учеб. для вузов / А. П. Баскаков, Б. В. Берг, О. К. Витт и др. – 2-е изд., перераб. – М.: Энергоатомиздат, 1991. – 224 С.
7. Мещеряков В. В. Задачи по математике с MATLAB&SIMULINK. – М.:ДИАЛОГ - МИФИ, 2007. – 528 С.