Аннотация
В данной работе рассматривается подход к решению задачи составления расписания выполнения заданий, на множестве которых введен частичный порядок предшествования, основанный на применении островной модели генетического алгоритма с динамической настройкой параметров локального поиска. Помимо дочерних генетических алгоритмов основной модели, в данной работе рассматривается алгоритм искусственной иммунной системы, выступающей в роли отдельного контроллера развития островной популяции.
Введение
Планирование – процесс распределения вычислительных работ между процессорами, с целью уменьшения общего времени выполнения заданий. Важным аспектом подобных процессов является решение задач составления расписаний, которые, в общем случае, являются NP-трудными. В данной работе рассматривается задача составления расписания заданий, на множестве которых введен частичный порядок, заданный ориентированным графом без циклов. Задания представляются вершинами графа, в то время, как зависимости между заданиями – его дугами. Наличие частичного порядка существенно усложняет задачу и требует внесения множества корректив в алгоритмы построения расписания. В данной работе рассматривается гибридный алгоритм, включающий идеи как эволюционных процессов [1], так и механизмов работы искусственных иммунных систем [5].
Пусть
– число заданий, подлежащих выполнению; 
– число процессоров, работающих параллельно; 
– время начала выполнения задания i на процессоре j, 
, 
; 
– время выполнения задания i, . В единицу времени процессор может выполнять не более одного задания. Прерывания выполнения заданий запрещены. На множестве заданий введен частичный порядок: задание 
предшествует заданию 
(
) тогда и только тогда, когда 
, где 
; 
. Необходимо составить расписание минимальной длины.
Основой разработанного алгоритма является островная модель генетического алгоритма, особи которой представлены следующей структурой данных. Пусть
– взаимно однозначное отображение имен заданий, подлежащих выполнению (
), на множество индексов 
, 
– взаимно однозначное отображение множества имен процессоров (
) на множество индексов 
. Рассматривается ассоциативный массив длины , индексы которого принадлежат множеству , а значения – множеству . Исходя из приведенных выше отображений, данный массив позволяет однозначно соотнести задание и процессор, на котором это задание будет выполняться. Для оценки приспособленности особей выбрана широко распространенная целевая функция
, показывающая длину расписания, полученного путем восстановления расписания из хромосомы особи. Генетические алгоритмы имеют вероятностный характер. Поэтому, при разных запусках, популяция может сходиться к разным допустимым решениям, которые в той или иной степени близки к оптимуму. Кроме того, нередки случаи, когда одни статически заданные параметры работы отдельного алгоритма приводят к длительной сходимости, в то время как другие позволили бы быстро получить субоптимальное, или даже оптимальное решение. Для обхода этих и многих других проблем классической схемы генетического алгоритма была разработана островная модель [2].
В данной версии гибридного алгоритма островная модель базируется на пяти параллельно развивающихся популяциях, четыре из которых основаны на «локальных» генетических алгоритмах, а одна – на алгоритме искусственной иммунной системы. Координация действий локальных алгоритмов возлагается на алгоритм-контроллер, посредством которого производится миграция особей из популяции в популяцию и контроль жизненного цикла развития популяций в целом.
Работа алгоритма-контроллера начинается с генерации случайных особей для начальных популяций. Как только все начальные популяции сгенерированы, алгоритм-контроллер запускает локальные алгоритмы и переходит в режим ожидания завершения их выполнения.
Когда все локальные алгоритмы завершили выполнение, начинается основная работа алгоритма-контроллера. Из каждой результирующей популяции выбирается третья часть лучших ее представителей (но не менее одного) посредством алгоритма селекции методом имитации отжига [3]. Выбранные особи образуют множество мигрирующих особей. Далее алгоритм-контроллер проводит по три итерации кроссовера между случайно выбранными парами особей этого множества, если его мощность больше единицы. Кроссовер внутри локального генетического алгоритма проводится согласно установленной стратегии развития популяции, тем самым приводя особей к одному классу. Кроссовер же внутри алгоритма-контроллера выполняет операции над особями разных классов, что приводит к получению «нестандартных комбинаций».
Завершает обработку популяций локальных алгоритмов фаза миграции, осуществляемая путем применения алгоритмов заменяющего и вероятностного обновлений.
После обновления популяций локальные алгоритмы перезапускаются, и описанный цикл повторяется.
Критериями остановки алгоритма-контроллера являются: проведение максимально возможного количества итераций и достижение максимально возможного количества неулучшающих итераций. Оба эти параметра являются предустановленными для алгоритма-контроллера.
Обычно, в начале работы алгоритма построения расписания в разрезе данной задачи, задания, не имеющие предков относительно графа частичного порядка, считаются независимыми, и построение расписания начинается с них. Такой метод в данной работе условно называется методом «сверху-вниз». Построенное этим методом расписание выглядит так:
Рисунок 1. Расписание, полученное методом ”сверху-вниз”.
Два из четырех локальных генетических алгоритма развития популяций используют именно этот метод.
Другой метод – «снизу-вверх» – строит расписание, начиная с листовых вершин графа частичного порядка. Для этого все зависимости обращаются, образуя новый граф частичного порядка, относительно которого и работает механизм построения расписания. Расписание, полученное таким способом, имеет в некотором смысле обратный вид:
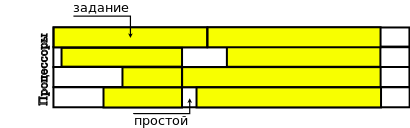
Рисунок 2. Расписание, полученное методом ”снизу-вверх”
Этот метод используют другие два локальных генетических алгоритма.
Таким образом, комбинируя особей популяций, развивающих по этим стратегиям, делается попытка получить более ”компактную укладку” заданий в расписании.
Важной особенностью локальных генетических алгоритмов, применяемых в данной работе, является наличие фазы локального поиска с динамической настройкой параметров, где под параметрами понимаются коэффициенты усиления и расширения поиска [4], базирующиеся на введенной ранее структуре данных, описывающей особь. Введение данной фазы позволило получать более приспособленных особей в пределах каждой отдельной итерации генетического алгоритма.
Пятый алгоритм развития популяции особей основан на идеях искусственной иммунной системы.
Искусственные иммунные системы (ИИС) – это адаптивные алгоритмы и системы алгоритмов, работа которых основана на идеях, взятых из наблюдений за принципами функционирования естественных иммунных систем [5]. При гибридизации ИИС с другими алгоритмами, чаще всего рассматривается лишь часть всего процесса работы естественной иммунной системы, наиболее подходящая под специфику конкретной задачи. В данной работе используются такие модели ИИС, как отрицательный отбор, отвечающий за регуляцию жизненного цикла популяции, и клональная селекция, выполняющая функции алгоритма развития популяции и механизма локального поиска [6].
Для запуска алгоритма иммунной системы необходима начальная популяция, которая, как правило, генерируется случайным образом. Работу иммунной системы можно условно разделить на два состояния: пассивное и активное. В пассивном состоянии иммунная система «просматривает» решения с целью обнаружения патогенов – решений, значения целевой функции которых превышает среднее значение целевой функции по популяции. При выявлении патогенов алгоритм иммунной системы переключается в активную фазу, где основным алгоритмом является клональная селекция [6]. В целом, клональная селекция похожа на генетический алгоритм без кроссовера и предельно высокой вероятностью мутации, но есть и существенные отличия: генетический алгоритм имеет тенденцию к концентрации особей популяции в окрестности наилучшего, возможно, локального оптимума, в то время, как клональный алгоритм позволяет получать разнообразное множество локальных решений, в том числе и глобальный оптимум. Кроме того, важной отличительной особенностью механизма работы клонального алгоритма является использование значения аффинности антитела при подсчете степени мутации, которую нужно применить к конкретному антителу для улучшения значения целевой функции. При обнаружении семейства патогенов решения, им соответствующие, клонируются, и клоны подвергаются мутации, причем степень мутации
зависит от величины невязки значения целевой функции каждого отдельного антитела и средней оценки популяции: 
где
– значение целевой функции «наиболее активного» патогена из рассматриваемого множества, – размерность антитела, 
– среднее значение целевой функции по популяции, 
– аффинность данного антитела. После мутации из полученного множества клонов выбираются наилучшие относительно аффинности. Для каждого изначального патогена, находящегося в популяции, ищется мутировавший клон, значение аффинности которого выше текущего. Если такой клон найден – происходит замещение. В противном случае патоген остается в популяции1. Для увеличения средней аффинности популяции применяется алгоритм иммунного локального поиска, которой является в некотором смысле обратным к алгоритму, описанному выше. Если центральной частью предыдущего алгоритма являлись процессы обнаружения антител, имеющих наименьшую аффинность, и взаимодействия с ними, в данном алгоритме делается упор на поиск наиболее приспособленных антител. Из популяции выбирается группа решений, имеющих наилучшие значения целевой функции относительно всей популяции, и производится процедура клональной селекции, применяемая к каждому антителу этой группы. Кроме того, после создания популяции мутировавших клонов, заменяются не «родительские» антитела, а патогены, имеющие аффинность ниже, чем у представителей множества мутировавших клонов.
Заключение
Результаты работы описанного гибридного алгоритма сравнивались с результатами работы жадного алгоритма (алгоритм критического пути), списочного алгоритма (дающего оптимальное решение при наличии двух процессоров) и метода ветвей и границ построения расписаний. Кроме того, для тестирования алгоритма на задачах исключительно большого размера, где выявление оптимума посредством метода ветвей и границ является практически невыполнимой операцией, был разработан модуль генерации задач с заранее заданной длиной расписаний. Во всех тестовых случаях решения, полученные разработанным алгоритмом, были оптимальными или близкими к оптимуму, а использование параллельной модели позволило значительно ускорить выполнение алгоритма. Так же были выявлены ограничения алгоритма иммунной системы, что дало развитие новой ветви исследования, направленной на построение многоуровневой параллельной модели.
Литература
1. И. Л. Каширина. Введение в эволюционное моделирование // Федеральное агентство по образованию Воронежский государственный университет, Воронеж. — 2007.
2. Darrell Whitley, Soraya Rana, and Robert B. Heckendorn. The island model genetic algorithm: On separability, population size and convergence // Journal of Computing and Information Technology. — 7:33–47, 1998.
3. Rakesh Kumar and Jyotishree. Effect of annealing selection operators in genetic algorithms on benchmark test functions // International Journal of Computer Applications . — (0975 – 8887), 40 – No.3, 2012.
4. Guang-Yuan Liu, Yi He, Yonghui Fang, and Yuhui Qiu. A novel adaptive search strategy of intensification and diversification in tabu search // Neural Networks and Signal Processing. — Proceedings of the 2003 International Conference on volume 1, pages 428–431 Vol.1, 2003.
5. Steven A. Hofmeyr and S. Forrest. Architecture for an artificial immune system. — 2000.
6. В. И. Литвиненко. Применение алгоритма клонального отбора для решения систем алгебраических уравнений // Математичнi машини i системи. — 2006.