Решение задачи составления расписания занятий в университете с использованием эволюционных алгоритмов
Авторы: Mohammed Aldasht; Safa Adi; Mahmoud Alsaheb; Mohammad Abu Qopita
Источник: ResearchGate University Course Scheduling Using Evolutionary Algorithms
Перевод: Безуглый М.А.
Резюме
В этой работе представлены новые эвристические подходы, основанные на эволюционных алгоритмах, имеющие практическое значение для решения проблемы составления расписания в университете, где подходящие и удобные расписания необходимы. Идея работы состоит в том, чтобы использовать эволюционное программирование, которое является стохастической стратегией оптимизации, подобной генетическим алгоритмам. Основное различие в том, что эволюционное программирование требует взаимосвязи между родителями и их потомками, вместо того, чтобы стремиться имитировать определенные генетические операторы, такие как наблюдаются в природе. Эта работа начинается с определения проблемы и определения ограничений, учитывая которые должно быть найдено решение. Таким образом, модель проблемы описывается рядом курсов, помещений, преподавателей, и студенческих групп. Наконец, предложенная методология используется в одном из четырех колледжей нашего университета. Результаты показывают, что наша методология больше подходит, для исследования области описываемой проблемы, которая позволяет составить оптимальное расписания времени, чем выполненные вручную. Полученные результаты также показывают, что предложенные решения могут решить много трудностей связанных с составлениями расписания.
Ключевые слова – планирование курса университета; расписание; эволюционные алгоритмы.
Введение
Университетское планирование курса можно рассмотреть, как пример так называемой проблемы расписания, которая является, утомительной работой, в каждом академическом институте расписание составляется один или два раза в год. Проблема включает планирование занятий, студентов, учителей и помещений в постоянные временные интервалы, которые удовлетворяют ряд негибких ограничений и минимизирует стоимость ряда гибких ограничений [1]. Эта проблема является NP-полной или даже NP-трудной проблемой [15]; это подразумевает, что есть не известный многочленный алгоритм времени, который может гарантировать нахождение лучшего решения [2]. Традиционно, составление расписания вручную испытанный метод, который не гарантирует надежного решения. Даже если действительное решение найдено, большая вероятность потери намного лучших решений. Эти проблемы имеют мотивированные научные исследования, для развития автоматизированных методов решения [1] [3] [4] [6-10] [13].
В этой работе освещена проблема университетского планирования курса; и включает процесс назначения набора занятий и ряда преподавателей к данному набору курса, принимая во внимание ряд негибких и гибких ограничений. Пример, негибких ограничений: человек не может быть в разных местах в одно и тоже время. Другой пример – это полные ресурсы, ассигнованные временному интервалу, должны быть меньше или равны ресурсам, которые доступны в тот временной интервал. Гибкие ограничения, с другой стороны, у учителя или у группы студентов не должно быть последовательных занятий в разных местах [4] [5].
Оставшаяся часть статьи структурирована следующим образом: Раздел II описывает соответствующие работы в этой области. Раздел III описывает моделирование задач, которые важны для описания того, как осуществить решение проблемы. Затем Раздел IV описывает эволюционный алгоритм, который используют для исследования области поиска, определенной модели в Разделе III. Раздел V описывает полученные результаты эксперимента и соответствующие комментарии и наконец, Раздел VI включает в себя предполагаемые результаты и выводы.
Вспомогательная работа
Есть много решений, предложенных в литературе для решения такой проблемы. В [1] предложены два подхода решения проблемы: (1) ИГА (Измененный Генетический Алгоритм) и (2) ОГA (Объединенный Генетический Алгоритм). Авторы стремились улучшить алгоритм работы, используя измененные генетические операторы или объединенный генетический метод, соответственно. В [6] отчет авторов о разработке общего инструмента под названием NExshed; этот инструмент как программное расширение для Excel Microsoft. В [7] авторы использовали гибридный алгоритм решения проблемы составления расписания. Этот алгоритм объединяет целое число программного подхода, эвристический и измененный моделируемый алгоритм отжига. В [8] представлена методика перевода требований курса на относительную формулу. Таким образом, проблема планирования была решена с помощью существующих инструментов, таких как Allay Analyzer. В [9] авторы обращаются к академическому планированию курса в сетевой окружающей среде, используя информаторов искусственного интеллекта в пределах урегулирования содержания системы. В [10] авторы изучают подходы, основанные на методе отжига. Работа включает отжиг поля осредненных величин, моделируемый отжиг с тремя различными графиками охлаждения и использованием основанных правил в системе препроцессора, чтобы обеспечить подходящие инициалы решения отжига. В [3] предложена система многоагентного планирования для университетского курса. В [4] авторы чтобы решить проблему улучшили полный подход, используя ЛЦП (Линейное Целое число Программирования). Развитая и решенная модель ЛЦП использует 3 современных решающих устройства основанных на ГA (Генетический Алгоритм) и БМВ (Булев Метод Выполнимости).
Очевидно, что выполнение всевозможных различных эволюционных алгоритмов, прежде всего ГА, в решении проблемы составления расписания университетского курса была широко изучена. Эти алгоритмы зависят от своих специальных операторов, т.е., мутация и переход. Поскольку область поиска проблемы очень велика, более общий подход должен гарантировать обширное исследование и игнорировать частную минимальную проблему, которая является частой в таком месте поиска. В этой статье наш подход представляет простой способ для решения и обширного исследования для области поиска.
С другой стороны, большинство вышеупомянутых подходов моделируют проблему согласно ряду различных параметров, подходящих для данного учреждения. Поэтому, частные правила учреждений и условия, связанные с их расписаниями необходимо рассматриваыть при решении задачи составления расписания.
Описание проблемы и моделирование
Колледж Административных Наук и Информатики при Политехническом университете в Палестине рассматривается как прототип. В этом колледже есть четыре академических программы. Курсы предлагаются в начале каждого семестра больше чем для двадцати студенческих групп. Там существует 5 рабочих дней в неделю (с воскресенья по четверг). По воскресеньям, вторникам и четвергам девять 60-минутных временных интервалов в день. По понедельникам и средам шесть 90-минутных временных интервалов в день.
Чтобы решить проблему, шесть различных наборов были определенны: студенты, преподаватели, курсы, аудитории, временные интервалы и набор ограничений. Затем проблема сформулирована как: P = {S, T, C, R, L, O}. Где: S = {s1, s2, …, Сn} является множеством студенческих групп. T = {t1, t2, …, tj} преподавательский коллектив. C = {c1, c2, … …, cn} множество предлагаемых курсов. C – вектор, используется, чтобы описать следующее: группа студентов, которым предлагается данный курс, число курса, секция, максимальный объем секции, преподаватель секции, число теоретических часов курса, число практических часов курса, тип практических часов и наконец период, который преподаватель должен присутствовать в лаборатории. R = {r1, r2, ….., rm} множество аудиторий. R – вектор, описывает максимальный объем данной аудитории, в комнате есть информация, указывающая на тип аудитории. L = {l1, l2, ….., lk} множество временных интервалов недели. O = {o1, o2, … …, OQ} является множеством ограничений. Где oi: размер штрафа (стоимость) ограничения. За нарушение негибкого ограничения размер штрафа больше, чем за нарушение гибкого ограничения.
Во множестве решений проблемы каждое решение оценено, как индикатор для определения адекватности решения.
А. Определение решения
Решение представлено как: G = {g1, g2, …., gw}. Где G – множество генов, из которых состоит хромосома. Как показано на рисунке 1, каждый ген – вектор включающий следующее: номер курса, номер аудитории, практический временной интервал, номер лаборатории и временной интервал теоретического времени.

Рисунок 1 – Особь
Как упомянуто во введении, в университетском курсе проблема расписания, представлена как, NP-трудная. Средства, поиска решения такой проблемы очень сложные. Таким образом, каждой секции курса будет нужна подходящая аудитория и/или лаборатория и время, которое подходило бы для студенческих групп и лектора. Чтобы уменьшить время поиска и сложность, алгоритм случайно выбирает подходящее место для секции курса. Таким образом, для оптимизации решения, принимают во внимание негибкие и гибкие ограничения для студентов и лекторов.
Особь составлена таким образом, что каждый ген имеет различный диапазон вариантов, выбирая временной интервал и класс; таким образом секция курса, представленная в гене G1, имеет максимальное количество вариантов, доступных, как случайный отбор классов и временных интервалов. Секция курса представленный в гене G2 на 1 выбор меньше, чем доступные для гена G1 и последний ген у Gw наименьшее количество вариантов.
У выбранного экземпляра, есть максимум 14 классов и 7 лабораторий. Кроме того, в течение недели, там проходит 41 теоретическое занятие по одному часу каждое и 13 практических занятий по 3 часа каждое. Это означает максимальный объем помещения 41*14 = 574 теоретических занятия, а максимальный объем лаборатории 13*7 = 91 практических занятия. На рисунке 2 важность 1 значение временного доступного интервала и 0 значение недоступного временного интервала.

Рисунок 2 – Временные интервалы
В. Ограничения
Ограничения разделены на негибкие ограничения, которые должны быть удовлетворены и гибкие ограничения который могут быть удовлетворены. Набор ограничений и их нагрузки следующие:
Негибкие ограничения:
- У преподавателя не должно быть больше одной лекции в определенный временной интервал;
- Преподавателю должны назначаться лекции только в удобное для него время;
- Студентам нельзя назначить больше одной лекции в определенный временной интервал;
- Количество студентов на лекции должно быть меньше или равняться максимальному объему класса;
- В любой временной интервал студенческая группа может занимать только определенную аудиторию.
У гибких ограничений стоимость нарушения намного меньше.
Гибкие ограничения:
- У студентов не должно быть больше чем трех занятий непрерывно;
- У преподавателей не должно быть большого перерыва между лекциями;
- У преподавателей не должно быть ежедневных поздних занятий;
- У группы студентов не должно быть последовательных занятий в разных корпусах.
5. У студентов не должно быть большого перерыва между лекциями.
Эволюционный алгоритм
Широкий спектр алгоритмов может быть классифицирован как эволюционный. Поскольку большинство предложенных алгоритмов зависят от их специальных операторов мутации и перехода, мы решили проектировать эволюционный алгоритм, который не содержит оператора скрещивания. В этой работе, ЭП (эволюционное программирование), является стохастической стратегией [16] оптимизации. Основное различие между ЭП и ГА – в том, что типичный ГA включает кодирование проблемных решений как цепочка представительных знаков, т.е., двойное представление [11] [12]. В ЭП, представление приходит из природы проблемы, которая представляет более простое решение. Кроме того, ЭП в общем зависит от процесса мутации, а не от перекомбинации (кроссинговера).
Эволюционный программный процесс начинается с отбора родителей. Затем родительские свойства видоизменяются, чтобы произвести потомков, которые увеличат популяцию. Затем алгоритм отказывается от нежизнеспособных особей и выбирает лучших из популяции, чтобы использовать их в следующем поколении.
Метод ЭП состоит из следующих шагов [16]:
- Инициализировать популяцию;
- Определить жизнеспособность особей;
- Вычислить фитнес функцию для каждой особи;
- Случайная мутация каждого «родителя» в популяции;
- Оценка «родителей» и «потомков»;
- Отбор особей для следующей популяции;
- Вернуться к 2 пункту, пока не выполнены условия остановки алгоритма.
В этой работе упомянутые шаги могут быть описаны следующим образом:
Шаг 1: загрузить необходимые данные из разных файлов, в которых указаны временные интервалы студенческих групп, временные интервалы учителей и временные интервалы учебных аудиторий. Алгоритму должны быть известны данные о доступности времени студентов, учителя и аудиторий. Первоначально, предполагается, что студентам доступно все время в течении пяти рабочих дней недели, в то время как у учителей и аудиторий могут быть некоторые ограничения по времени.
Шаг 2: значение измеряется как сумма значений каждого гена в особи. Штраф за нарушение ограничений.
Шаг 3: фитнес-функция f (x) = 1 / (стоимость(x) +1). Где стоимость(x) сумма значений генов в особи.
Шаг 4: случайная модификация происходит над генами, чья стоимость больше 0. В нашем алгоритме каждая особь переупорядочивается в соответствии со стоимостью генов. Где гены с нулевой стоимостью размещены в начале особи. Затем, мутация начинается с первого гена стоимость которого больше нуля. Эта мутация называется ПМ
(Переупорядоченные Мутация).
Шаг 5: Следующим шагом является выбор особей для следующей популяция в зависимости от значения фитнес-функции. В нашем алгоритме используется выбора с помощью рулетки и элитарный отбор.
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА
Наше приложение выполнено, на языке программирования C на компьютере с двухъядерным процессором Intel (R) XeonTM с кэшем 3 уровня 512 Кб, оперативная память 2 ГБ под управлением Linux. Для нашего эксперимента взяты реальные данные, из базы данных Палестинского Политехнического Университета. Данные кодируются в числа и хранятся в текстовых файлах, которые используются в качестве входных данных в программе.
Результат
Поскольку время выполнения нашего алгоритма значительно зависит от использования случайной функции, на рисунке 3 показана природа случайной функции, которая используется в наших экспериментах. Очевидно, что функция имеет равномерное распределение с мат ожиданием 49.96362 и дисперсией 832.741.

Рисунок 3 – Случайная функция распределения
Следующие числа, т.е., рисунок 4, 5 и 6, для эксперимента, который сделан с численностью популяции 30 особей и 500 поколениями. Эксперимент был проведет трижды. Затем было выделено среднее число, это показано на рисунках 4, 5 и 6. В ходе этого эксперимента, был найден лучшая особь в поколении 228. Полное выполнение составляло приблизительно 9 минут.
На рисунке 4 показана зависимость между числом поколений и средняя приспособленность в поколение.
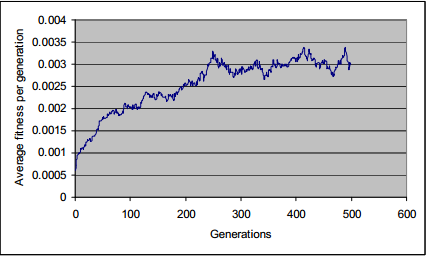
Рисунок 4 – Среднее значение фитнес-функции
На рисунке 5 показаны изменения средней лучшего значения по поколению. Таким же образом рисунок 6 показывает отношение между числом поколений и средним значением фитнес-функции.
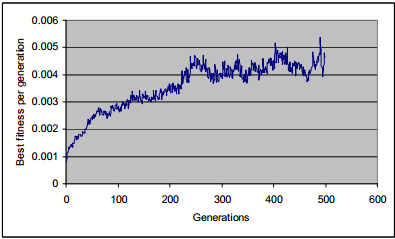
Рисунок 5 – Лучшее значение фитнес-функции
Таким же образом, на рисунке 6 показано соотношение между число поколений, и среднее значение лучшей фитнес-функции в поколении.
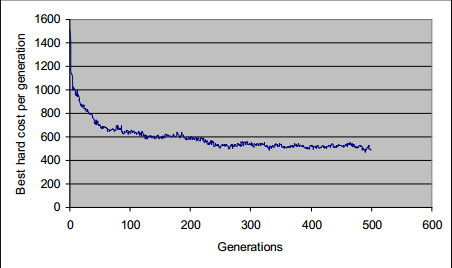
Рисунок 6 – Значение фитнес-функции
Тестирование
Для тестирования, были выбраны 20 студентов, которые должны были ответить на 5 вопросов следующим образом:
- Желаемые зачетные часы для регистрации;
- Зачетные часы с использованием графика составленного вручную;
- Зачетные часы с использованием предложенного графика;
- Степень удовлетворения ручным графиком;
- Степень удовлетворения предложенным графиком.
Результаты представлены в таблице 1.
Таблица 1 – Результаты опроса
|
|
Образец |
Студенты, которые имели регистрационные проблемы (с часами) |
Студенты, у которых нет проблем (с часами) |
|
|
Процент |
100% |
35% |
65% |
|
|
Средние количество кредитных часов, необходимых для студента |
16.6 |
17.14 |
16.3 |
|
|
Средние кредитных часов (ручное расписание) |
15.7 |
14.4 |
16.4 |
|
|
Средние кредитных часов (предлагаемый график) |
16.5 |
16.7 |
16.4 |
|
|
Удовлетворение графиком, составленным вручную |
Удовлетворенный или очень довольны |
60% |
57% |
62% |
|
Не удовлетворены |
40% |
43% |
38% |
|
|
Удовлетворение предлагаемым графиком |
Удовлетворенный или очень довольны |
80% |
100% |
70% |
|
Не удовлетворены |
20% |
0% |
30% |
|
Выводы
В этой статье предложенный алгоритм ЭП, пытается решить проблему планирования курса занятий в ВУЗе. Алгоритм способен, найти удовлетворительные решения этой проблемы. Результат можно получить благодаря выполнению следующих условий:
- Должна быть введена подходящая проблемная модель для широкого ряда учебных учреждений;
- Эволюционный алгоритм предложен со специальным оператором мутации назван РM, который приводит к оптимальным решениям;
- Алгоритм реализует методологию поиска для нахождения результата из всего пространства поиска решений;
- Предложенная методология применена на реальных наборах данных и может быть расширена, для использования другими учреждениями;
- Результаты показывают, что наша методология может дать расписания максимум с 97%-м выполнением гибких ограничений и до 100%-е выполнение негибких ограничений;
- Тестирование показывает, что наша работа решает проблемы составления лучше больше чем для одной трети студентов;
- Кроме того, таблица 1 показывает, что предложенный нами график удовлетворяет студента больше, чем график, составленный вручную.