Аннотация
Чеканин В.А., Чеканин А.В. Модель управления свободными пространствами контейнеров в задаче ортогональной упаковки объектов Рассматривается задача ортогональной упаковки объектов в контейнерах произвольной размерности. Предлагается новая модель управления свободными пространствами контейнеров. Показана эффективность разработанной модели потенциальных контейнеров на примере задачи трехмерной ортогональной упаковки объектов.
Ключевые слова: задача ортогональной упаковки, задача контейнерной упаковки, распределение ресурсов, оптимизация
Введение
Задача ортогональной упаковки объектов представляет собой задачу оптимального размещения заданного набора ортогональных объектов в ортогональных контейнерах при выполнении следующих условий [11-12]:
1) ребра размещенных в контейнере ортогональных объектов параллельны ребрам этого контейнера;
2) упакованные объекты не перекрывают друг друга;
3) упакованные объекты не выходят за границы контейнеров. К решению этой задачи сводится множество практических задач распределения ресурсов [1, 5-8], в частности, задач календарного планирования, контейнерной перевозки грузов [2, 9] и др.
Для управления свободными пространствами контейнеров в задаче ортогональной упаковки могут быть использованы следующие модели представления объектов в контейнерах: блочная [3], узловая и модель «виртуальные объекты» [4, 10], обеспечивающая наиболее быстрое среди прочих моделей размещение объектов. Основной недостаток модели «виртуальные объекты» – существование вероятности образования при решении задач упаковки размерности выше двух локальных пустот в контейнерах, снижающих плотность размещения объектов в контейнерах [10].
Модель потенциальных контейнеров
Разработанная модель потенциальных контейнеров является развитием модели «виртуальные объекты». В основе этой модели лежит модель управления свободными пространствами контейнера (так называемыми потенциальными контейнерами), которая включает алгоритм образования потенциальных контейнеров и алгоритм поиска и удаления вложенных потенциальных контейнеров. Модель потенциальных контейнеров в отличие от модели «виртуальные объекты» описывает все существующие свободные пространства размещаемого контейнера, что исключает вероятность образования неконтролируемых локальных пустот контейнера. На рис. 1 приведены возникающие при размещении трехмерного объекта потенциальные контейнеры, описывающие все существующие свободные для размещения пространства контейнера.
Блок-схема алгоритма размещения заданной последовательности объектов в контейнерах при использовании модели потенциальных контейнеров приведена на рис. 2.

Рис. 1. Потенциальные контейнеры в задаче трехмерной упаковки
Вычислительный эксперимент
Исследование эффективности модели потенциальных контейнеров проводилось при решении задачи упаковки 500 трехмерных объектов шести различных типов в ортогональный контейнер с габаритными размерами 300×100×100. Параметры решаемой задачи приведены в таблице 1.
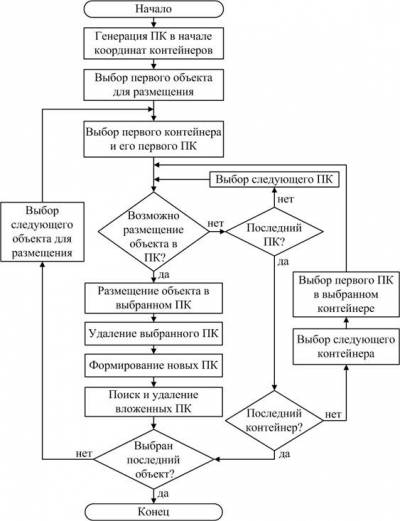
Рис. 2. Блок-схема алгоритма размещения объектов в модели потенциальных контейнеров (ПК)
В качестве показателя размещения объектов в одном контейнере выбрана относительная плотность размещения объектов S, которая рассчитывается в виде отношения объема размещенных в контейнере объектов к объему V* описанного вокруг полученной D -мерной упаковки D мерного параллелепипеда:
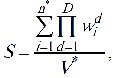
где n* – число размещенных в контейнере объектов; wid – габаритный размер объекта i, измеренный в направлении оси d контейнера; D – размерность решаемой задачи упаковки. Значение относительной плотности размещения S=1 соответствует наиболее плотному размещению объектов.
Таблица 1. Параметры тестовой задачи трехмерной упаковки
|
№ |
Габаритные размеры размещаемых объектов |
Количество |
|
1 |
50×30×10 |
20 |
|
2 |
10×30×60 |
20 |
|
3 |
25×30×25 |
20 |
|
4 |
25×25×25 |
20 |
|
5 |
10×10×10 |
20 |
|
6 |
5×5×5 |
400 |
Проведенный вычислительный эксперимент (таблица 2) показал, что разработанная модель потенциальных контейнеров обеспечивает более плотное размещение объектов по сравнению с моделью «виртуальные объекты».
Таблица 2. Относительная плотность размещения S
|
Модель «виртуальные объекты» |
0.727 |
|
Модель потенциальных контейнеров |
0.810 |
Заключение
Предложена новая модель представления ортогональных объектов в контейнерах, описывающая все существующие свободные пространства размещаемых контейнеров. Проведенные исследования продемонстрировали эффективность разработанной модели потенциальных контейнеров и ее применимость для управления свободными пространствами контейнеров при решении задач ортогональной упаковки объектов.
СПИСОК ЛИТЕРАТУРЫ
1. Митрофанов В.Г. Интегрированные производственные системы // Вестник МГТУ «СТАНКИН». 2008. № 1. С. 65-67.
2. Мухачева Э.А., Бухарбаева Л.Я., Филиппов Д.В., Карипов У.А. Оптимизационные проблемы транспортной логистики: оперативное размещение контейнеров при транспортировке грузов // Информационные технологии. 2008. № 7. С. 17-22.
3. Филиппова А.С. Моделирование эволюционных алгоритмов решения задач прямоугольной упаковки на базе технологии блочных структур // Информационные технологии. 2006. № 6. Приложение.
4. Чеканин В.А. Эффективное решение задачи двухмерной контейнерной упаковки прямоугольных объектов // Вестник компьютерных и информационных технологий. 2011. № 6. С. 35-39.
5. Чеканин В.А., Ковшов Е.Е. Моделирование и оптимизация технологических операций в промышленном производстве на основе эволюционных алгоритмов // Технология машиностроения. 2010. № 3. С. 53-57.
6. Чеканин В.А., Ковшов Е.Е. Систематизация и анализ структур данных при автоматизации управления складом на основе генетических алгоритмов // Известия высших учебных заведений. Проблемы полиграфии и издательского дела. 2008. № 5. С. 42-51.
7. Чеканин В.А., Ковшов Е.Е., Хуэ Н.Н. Повышение эффективности эволюционных алгоритмов при решении оптимизационных задач упаковки объектов // Системы управления и информационные технологии. 2009. № 3. С. 63-67.
8. Чеканин В.А., Чеканин А.В. Исследование генетических методов оптимизации распределения прямоугольных ресурсов // Материалы 2-й международной научно-практической конференции «Современное машиностроение. Наука и образование» – СПб.: Изд-во Политехн. унта. 2012. C. 798-804.
9. Чеканин В.А., Чеканин А.В. Оптимизация решения задачи ортогональной упаковки объектов // Прикладная информатика. 2012. № 4. С. 55-62.
10. Чеканин В.А., Чеканин А.В. Эффективные модели представления ортогональных ресурсов при решении задачи упаковки // Информационно-управляющие системы. 2012. № 5. С. 29-32.
11. Dyckhoff H. A typology of cutting and packing problems // EJOR. 1990. Vol. 44. P. 145-159.
12. Washer, G., Haubner, H., Shumann, H. An improved typology of cutting and packing problems // EJOR. 2007. Vol. 183. N. 3. P. 1109-1130.