Известная задача плотной упаковки трехмерных объектов для их транспортировки в контейнерах, грузовиках, вагонах и трюмах постоянно расширяет области своего применения. Проблема трехмерной упаковки становится все более актуальной в современной промышленности, особенно при использовании hi-tech технологий. Общая тенденция к микроминиатюризации требует более плотной упаковки и видоизменения компонентов в ограниченном объеме. Эта задача востребована и в машиностроении, где требования к компактности сборки узлов автомобилей стоят на первых местах. Трехмерная упаковка применяется и при разработке новых концепций построения и взаимного расположения узлов транспортных средств в машиностроении и космической промышленности. Но наиболее остро проблема уменьшения объема стоит в электронной промышленности при производстве чипов СБИС. Трехмерная трассировка электрических соединений с одновременным сжатием трехмерной топологии может дать значительный прирост в производительности электронных систем. В виде критерия могут выступать стоимость, безопасность, комфорт, быстродействие и др. Например, при производстве мобильного процессора компанией AMD остро стояла проблема тепловыделения. Без изменения архитектуры двумерная переупаковка топологии и соответствующая перетрассировка в первом слое позволили снизить потребление энергии на 20%, а производительность при этом возросла на 10%.
При решении рассматриваемой задачи удобно представлять область размещения и размещаемые элементы в виде параллелепипедов, грани которых совпадают по направлению с осями координат декартовой системы. Задачу можно свести к формированию последовательности заполнения заданной трехмерной области с учетом специфики сферы применения (критерия оптимизации, наличия (отсутствия) связей, числа вариантов размещения элементов в пространстве и т.д.). При этом оптимальное решение может гарантировать только алгоритм полного перебора вариантов размещения с факториальной временной сложностью. На практике необходимо решать задачи больших размерностей. В случае проектирования современных СБИС, даже с учетом регулярности структуры некоторых их фрагментов, число элементов размещения может достигать порядка 106 – 109. Ввиду NP-полноты рассматриваемой задачи, даже при малом числе элементов (15-20) решать ее целесообразно эвристическими, поисковыми, эволюционными или стохастическими методами для снижения аппаратных, вычислительных и временных затрат.
В данной работе рассмотрен эвристический алгоритм трехмерной упаковки несвязанных элементов, направленный на снижение трудоемкости вычислений. Алгоритм размещает элементы внутри параллелепипеда без учета привязки к силам тяготения. Это означает, что промежуточные элементы размещаются и на условных «стенах», и на «потолке». Порядок заполнения определяется сканированием плоскостей снизу вверх после получения решения. Задача решается в декартовой системе координат.
Постановка задачи
Имеется множество элементов для размещения A={ai| i=1,2,…,n}. Каждый элемент характеризуется тройкой чисел {xi,yi,zi}, где xi,yi,zi - габаритные размеры элемента. В ходе решения задачи положение элементов в
пространстве задается множеством S={si=(<x[1]i,y1i,z1i>, <x2i,y2i,z2i>) | i=1,2,…,n}, где
<x1i,y1i,z1i>, <x2i,y2i,z2i> - координаты углов элемента, самого близкого к началу
осей координат и самого удаленного соответственно . Так же имеется параллелепипед M={mx,my,mz}, где mx,my,mz – габаритные размеры области упаковки.
Возможны два критерия оптимизации:
1. N – число элементов, упакованных в заданный объем.
2. V – объем, требующийся для упаковки всех элементов. Для этих случаев существуют следующие ограничения:
1. Ни один элемент не может выходить за границы заданного объема:
x1i ≥ 0; y1i ≥ 0; z1i ≥ 0; x2i
≤ mx; y2i ≤ my; z2i ≤ mz;
2. Суммарный объем элементов не должен превышать объема области упаковки:
n
∑(xi ⋅ yi ⋅ zi )≤ mx ⋅ my ⋅ mz .
i=1
3. Отсутствие пересечений:
(x2i ≥ x1j & y2i ≥ y1j & z2i ≥ z1j) ∨ (x2i ≤ x1j & y2i ≥ y1j & z2i ≥ z1j) ∨
(x2i ≥ x1j & y2i ≤ y1j & z2i ≥ z1j) ∨ (x2i ≥ x1j & y2i ≥ y1j & z2i ≤ z1j) ∨
(x2i ≤ x1j & y2i ≤ y1j & z2i ≥ z1j) ∨ (x2i ≥ x1j & y2i ≤ y1j & z2i ≤ z1j) ∨ (x2i ≤ x1j & y2i ≥ y1j & z2i ≤ z1j) = 1 ∀ i ≤ n, j ≤ n (i≠j).
Критерием оптимизации является отношение суммы объемов всех элементов к общему объему упаковки [1]. Целевая функция имеет вид:
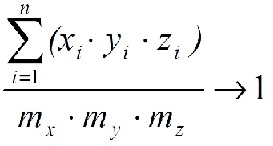
означающий, что необходимо стремится к уменьшению пустот в области упаковки. В идеальном случае, когда целевая функция равна 1, область упаковки заполнена на 100%.
Описание алгоритма. Алгоритм является последовательным. Очередной размещаемый элемент устанавливается в окончательное место на каждом шаге алгоритма.
В качестве основной использована следующая эвристика: для размещения на данном шаге должен быть выбран «самый неудобный для процесса размещения» (громоздкий, негабаритный) элемент среди еще не размещенных, так как поместить его в заданный объем с каждым следующим шагом будет все сложнее [2]. Для этого подсчитывается число возможных вариантов размещения каждого элемента, и для размещения выбирается элемент, для которого это число минимально. Необходимо также учитывать то, что параллелепипед, в общем случае, имеет шесть возможных вариантов ориентации в пространстве, когда его ребра параллельны осям координат (рис. 1).
Место размещения выбранного элемента и его ориентация в пространстве определяются так, чтобы суммарное число возможных вариантов размещения оставшихся элементов было максимальным. Для каждого элемента при подсчете числа вариантов его размещения рассматриваются все возможные положения в пространстве. Очевидно, что из шести полученных результатов необходимо выбрать вариант с наименьшим значением целевой функции.
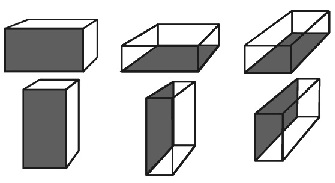
Рисунок 1
После размещения выполняется обычная компакция по трем осям.
Существуют два подхода к определению габаритов области для упаковки:
1) размеры области задаются до начала размещения, затем следует процесс последовательного размещения элементов (пока это возможно);
2) производится априорная оценка имеющегося набора параллелепипедов, на основании которой задается рабочая область с объемом, равным сумме объемов всех имеющихся элементов (ЦФ=1). В случае невозможности упаковки всех элементов в эту область, происходит ее увеличение на основе эвристик, описанных ниже. И так до тех пор, пока не будут упакованы все элементы.
Для второго случая предлагаются следующие эвристики. Отношения между сторонами области задаются на основании статистически набранных данных в зависимости от средней степени разногабаритности имеющихся элементов. Здесь под разногабаритностью понимается отношение наибольшего размера элементов к наименьшему. Увеличение области производится наращиванием наименьшей из ее сторон на единицу дискретности заданного трехмерного пространства.
Предлагаемые эвристики
Наибольшей трудоемкостью в алгоритме обладает подсчет числа возможных вариантов размещения. При стандартном подходе перебираются все возможные координаты угла элемента, ближайшего к центру координат и проверяется отсутствие перекрытия с другими элементами. Таких вариантов будет (mx - xi)(my - yi)(mz - zi), где i - номер рассматриваемого элемента.
Для этой подзадачи была предложена следующая эвристика. От границ области, включая уже стоящие там элементы, наращивается граница: по оси z на (zi – 1) клетку пространства в сторону плоскости z=0, по оси x на (xi – 1) клетку пространства в сторону плоскости x=0 и по оси y на (yi – 1) клетку пространства в сторону плоскости y=0. Объем полученной после этого области будет численно равен числу возможных вариантов размещения. В качестве примера рассмотрим двумерный случай (рис.2).

Рисунок 2
Число пустых клеток задает число возможных вариантов размещения. Определение границы является более простым процессом, так как все грани элементов представляются в виде плоскостей, а в случае проверки отсутствия пересечения элемента с уже установленными необходима проверка множества условий.
Для упрощения задачи предлагается учитывать следующую идею: размещать элемент целесообразно лишь в вогнутых трехгранных углах (рис.3).
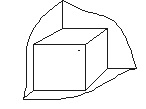
Рисунок 3
Если размеры элемента совпадают по двум или трем осям, то нет необходимости рассматривать все варианты его положения в пространстве (ориентации) при всех производимых вычислениях.
Применение данного алгоритма показало его эффективность для решения задач с числом элементов до 100 при квадратичной временной сложности алгоритма.
Вернемся к формулировке задачи, когда конечный объем не известен, т.е. задан набор элементов, который необходимо разместить в минимальный объем. В этом случае предлагается следующая стратегия: при неудачном размещении элементов в куб с объемом, равным сумме объемов всех элементов упаковки, объем куба умножается сразу на определенный коэффициент, зависящий от коэффициента разногабаритности (Кр) элемента. Здесь под коэффициентом разногабаритности понимается отношение максимального габарита среди всех элементов к минимальному:

Было произведено 10 экспериментов с N=16, последовательно задавая КР=1, 2, …, 10. Требуемый объем подбирался вручную. Экспериментально полученные данные приведены в табл. 1. При аппроксимации этой зависимости, получена следующая функция:
Кприращ. объема*=1+ Кр0,5
Таблица 1
|
Кр | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Кприращ. объема | 1,2 | 1,04 | 1,13 | 1,21 | 1,24 | 1,29 | 1,14 | 1,32 | 1,44 | 1,49 |
Теоретически полученная зависимость отражена в табл. 2.
Таблица 2
|
Кр | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|
Кприращ. объема* | 1,05 | 1,10 | 1,15 | 1,20 | 1,25 | 1,30 | 1,35 | 1,40 | 1,45 | 1,50 |
Из табл.2 видно, что теоретическая зависимость соответствует экспериментально полученной функции. Применение данной эвристики существенно сокращает число требуемых итераций при изначально неизвестном объеме.
Экспериментальные исследования эффективности алгоритма и его временной сложности (ВСА) проводились на наборах с мощностью, не превышающей N=10 для оценки эффективности (для возможности сравнения с результатами, полученными полным перебором) и до 100 при оценке ВСА. При проверке эффективности в 9 из 10 экспериментов алгоритм нашел решение, аналогичное полученному при полном переборе. В оставшемся случае разность значений целевой функции не превысила 6%. При оценке ВСА экспериментальный график лежал ниже теоретического, что объясняется использованием эвристик.
Алгоритм трехмерной упаковки реализован в программной среде Borland C++ Builder. Программа имеет дружественный и интуитивный графический пользовательский интерфейс. Для удобного просмотра динамики процесса и результатов решения в качестве инструмента визуализации была выбрана библиотека Open GL [3]. Благодаря этому, пользователь может вращать трехмерный вид упаковки с находящимися в нем элементами для нахождения наилучшего ракурса просмотра как «потянув» мышью за угол описывающего параллелепипеда, так и через линии скроллинга. Внешний вид рабочего окна программы представлен на рис 4.
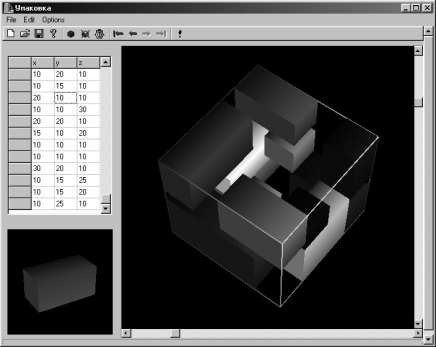
Рисунок 4
Редактирование списка элементов происходит в табличном режиме с трехмерной визуализацией редактируемого элемента в соответствующем окне. Для визуального различения элементов в объеме упаковки им присваивается цветовая последовательность. Полностью реализованы все перечисленные стратегии определения заранее неизвестного объема. Для выбора той или иной стратегии предусмотрены соответствующие пункты системы меню. Сохранять и загружать можно не только наборы элементов, но и готовые решения, что удобно при проведении исследований и сравнительного анализа результатов.
ЛИТЕРАТУРА
1. Бондалетов А.В. Двухмерная упаковка со связями. Части I, II. Известия ТРТУ, №3. Таганрог: изд-во ТРТУ, 1999.
2. Фионова Л.Р. Последовательный алгоритм плотной упаковки элементов. В кн.: Тезисы докл. Респ. науч.-техн. конф. «Автоматизация технического проектирования цифровой аппаратуры». Каунас: КПИ, 1981.
3. Тихонов Ю. Программирование трехмерной графики. СПб: БХВ, 1999. 432 с.
[1] Здесь использован метод «дважды ориентированной точки»: при описании плоского ортогонального контура последовательным обходом его точек ввиду последовательной повторяемости одной из координат на каждом шаге, целесообразно описывать точки контура
«через одну». Данная идея применена нами к трехмерному случаю описания