Аннотация
В данной работе предлагается алгоритм для расчета оптимального размещения элементов в область трехмерного пространства. За полиномиальное время он позволяет оптимально заполнить пространство и имеет высокую степень адаптивности к ограничениям, возникающим на практике. Особенность модифицированной эвристики является адаптивный механизм кодирования-декодирования информации и специальные генетические операторы.
Введение
Задача оптимального размещения объектов в ограниченном пространстве (задача трехмерной упаковки) широко применяются на практике в прикладной математике, криптографии, экономике, логистике, для нахождения решения оптимальной загрузки различных транспортных средств: самолетов, кораблей, железнодорожных вагонов и т.д. Наиболее перспективной областью применения можно считать транспортную логистику.
Было установлено, что данная задача является NP-полной. Как известно, все точные алгоритмы, решающие задачу об упаковке экспоненциальную временную сложность, что эквивалентно полному перебору всех возможных решений. Таким образом, поиск приближенных эвристик, которые за приемлемое время могут найти решение, близкое к оптимальному значению, и при этом имеют возможность адаптации для учета дополнительных условий, является актуальной задачей. К таким эвристикам относятся методы эволюционной адаптации, среди которых особое место занимают генетические алгоритмы (ГА). Использование ГА обусловлено простотой использования и достаточно глубокой изученностью данного класса поисковых механизмов. Основной проблемой является разработка алгоритма кодирования и последующего декодирования информации. В рамках данной работы задача представления исходной информации решается путем введения обратной польской записи.
Постановка задачи. Задана область трехмерного пространства (W, L, H). Также задано множество элементов N(wn,ln,hn). Требуется рассчитать точное положение элементов в заданном объеме таким образом, чтобы его заполнение было допустимым и эффективным, т.е. суммарный объем поместившихся элементов должен быть максимален.
F = (xmax - xmin) *(ymax- ymin) *(zmax- zmin) F→min
где точки ( xmin, ymin, zmin ) и ( xmax , ymax, zmax ) – точки, определяющие описывающий параллелепипед элементов.
Цель оптимизации – минимизация целевой функции. Введем правила размещения элементов:
1. Элементы могут иметь только форму параллелепипеда.
2. Упакованые могут быть только те элементы, которые полностью помещются в объем.
Кодирование решения. Для решения поставленной задачи был выбран генетический алгоритм. Основной проблемой при решении задач генетическим алгоритмом является кодирование и декодирование решений. Из всего многообразия разработанных подходов обратная польская нотация является наиболее эффективной [1]. Обратная польская нотация (ОПН) − форма записи выражений, в которой операнды расположены перед знаками операторов [2].
Обозначим каждый оператор числовым эквивалентом. Так как все блоки нумеруются целыми положительными числами, то целесообразно кодировать операторы отрицательными числами: «вперед» − “-1” (ось ОZ);
• «вправо» − “-2” (ось ОХ);
• «вверх» − “-3” (ось ОУ);
В соответствие с вышесказанным приведем пример кодирования решения для размещения блоков указанного на рис. 1.

Рисунок 1 – Размещение блок в трехмерном ограниченном пространстве
Представим данное размещение в виде дерева, изображенного на рис. 2. Корневая вершина соответствует конечному размещению. Листья дерева соответствуют размещаемым блокам, внутренние точки – операторам.

Рисунок 2 – Дерево размещения
В соответствии с данным деревом составим обратную польскую запись. Учитывая тот факт, что обратная польская нотация читается справа налево, получим следующую запись:
4 1 -3 5 2 3 -3 -1 6 7 -2 -1 -2
Закодированное решение (хромосома), соответствующее размещению (см.рис. 1), примет вид, приведенный на рис. 3.
| 4 |
1 |
3 |
5 |
2 |
3 |
3 |
1 |
6 |
7 |
2 |
1 |
2 |
| 25 |
25 |
|
25 |
36 |
36 |
|
|
20 |
20 |
|
|
|
| 30 |
30 |
|
30 |
44 |
44 |
|
|
18 |
18 |
|
|
|
| 35 |
35 |
|
35 |
40 |
40 |
|
|
67 |
67 |
|
|
|
| 15 |
15 |
|
15 |
30 |
20 |
|
|
60 |
60 |
|
|
|
| *m1 |
*m1 |
|
*m1 |
*m2 |
*m2 |
|
|
*m3 |
*m3 |
|
|
|
Рисунок 3 - Пример закодированного решения
Введем правило генерации хромосом: количество операторов должно быть на один меньше, чем число операндов стоящих перед ними [3]. Для генерации таких хромосом предлагается использовать модифицированный блок создания начальной популяции.
Также существует большая вероятность того, что полученные хромосомы могут не соответствовать определенным требованиям, например ограничениям габаритов контейнера. Поэтому необходима разработка модифицированных генетических операторов, которые могут учитывать все ограничения, заданные в задачи.
Модифицированный генетический алгоритм.
Общая структура генетического алгоритма приведена на рис. 4. На нулевой итерации инициализируется популяция, в соответствии с описанными выше правилами. Далее применяется модифицированный оператор редукции. Данный блок необходим для отсеивания хромосом заведомо не несущих в себе оптимального размещения («аутсайдеры») [3]. Модификация состоит в том, что с помощью данного блока «аутсайдеры» подлежат исправлению, если это возможно. Если такой возможности нет, то хромосомы удаляются их популяции. Предложены следующие эвристики исправления хромосом:
- Разворот множества грузов вокруг осей координат.
- Выделение часто используемых операторов. Так, например, если область имеет значение по длине больше чем значение по высоте и ширине то оператор «вправо» будет использоваться чаще, чем остальные. Значит, при исправлении данный оператор частично заменит операторы «вверх» и «вперед».
При таком походе размер популяции может быть отличен от исходного. Поэтому предусмотрена возможность дополнительной генерации особей, с последующей их проверкой.
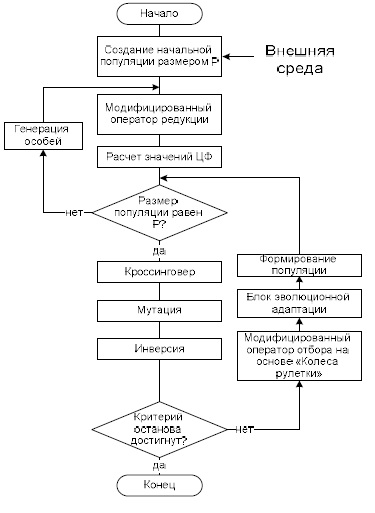
Рисунок 4 – Общая структура генетического алгоритма
Для создания нового генетического материала применяется частичносоответствующий оператор кроссинговера, однако точки разреза, выбираются на основе следующих правил:
1. Точки разреза устанавливаются только после нечетного гена. Благодаря этому в ряде случаев не нарушается правило соотношения числа операндов и операторов в паре хромосом [3].
2. Точка разреза не может стоять ближе, чем после 3 гена.
3. После установки точки разреза проверяется соотношение числа операндов и операторов. Если соотношение нарушено, точка разреза переопределяется заново, старое значение для данной пары хромосом фиксируется как неприемлемое.
Модификация оператора мутации состоит в перестановке двух генов одинакового типа, то есть ген-операнд может быть переставлен только на место генаоперанда, а ген-оператор может быть переставлен только на место гена-оператора[4].
Модификация оператора инверсии состоит в нахождении последовательно- сти генов, состоящих только из генов-операндов или генов-операторов, с максимальным Хемминговым расстоянием, которая перезаписывается в обратном порядке.
Предложенный модифицированный оператор отбора на основе «Колеса рулетки» аналогичен стандартному отбору на основе данного метода. Отличием является применение операторов исправления «аутсайдеров». Исправленные хромосомы также участвуют в процессе отбора.
Блок эволюционной адаптации предназначен для настройки и изменении порядка использования и применения различных генетических операторов и схем поиска с учетом изменения внешней среды. Результаты работы блока эволюционной адаптации оказывают непосредственное влияние на процесс перестройки текущей популяции альтернативных решений и создания на ее основе новой популяции [5].
Процесс поиска продолжается итерационно до достижения условий останова. Критериями останова может быть заданное число итераций, установленное время, достижение определенного качества решений.
Данный алгоритм был реализован на языке программирования C++. Проведен вычислительный эксперимент. В ходе проведения вычислительного эксперимента были установлены эмпирические зависимости, диапазоны изменения входных параметров и выработан ряд рекомендаций по их оптимальному выбору. Проведенные серии тестов и экспериментов позволили уточнить теоретические оценки временной сложности алгоритма. Временная сложность алгоритма O(n2).
Для применения данного алгоритма при решении практических необходимо вводить ряд правил и ограничений. Так, например, при решении задачи размещения грузов в транспортное средство необходимо учитывать маркировку груза, типизацию и т.д.
Заключение.
В данной работе авторами был предложен алгоритм решения задачи 3х-мерной упаковки удобный для применения на практике. Алгоритм находит приемлемое решение за полиномиальное время, что позволят использовать его в реальных задачах. Кроме того, модифицированные генетические операторы позволяют в большинстве случаев сразу получать решения удовлетворяющие условиям задачи, что помогает частично избежать значительных временных затрат на поиск и исправление «аутсайдеров».