Аннотация
В данной статье рассматривается проблема построения маршрутов следования транспортных средств с учетом трехмерного размещения грузов. Задача заключается в нахождении наикратчайшего пути следования транспортных средств по клиентам для доставки им товаров и загрузки этих товаров в транспортное средство, удовлетворяющих ограничениям трехмерной погрузки. Рассматривается проблема маршрутизации с помощью поиска с запретами и улучшенного локального поиска. Погрузка эффективно выполняется с помощью смешанного алгоритма, основанного на левом нижнем углу, который использует множественно представленную структуру данных. С помощью вычислительных экспериментов мы показываем, что наш подход способен производить качественные решения, сравнимые и лучше, чем предложенные в литературе.
1. Введение
Задача построения маршрутов следования транспортных средств(ТС) с трехмерным размещением грузов(3L-CVRP), характеризуется сочетанием задачи построения маршрутов и задачи упаковки контейнеров в трёхмерном пространстве. Проблема, которую представил Жандро и другие (2006), следует из потребности рассматривать погрузку прямоугольных коробок в автопарке, определяя маршруты таким образом, чтобы эти транспортные средства могли доставить предварительно упакованные товары ряду клиентов. Цель состоит в том, чтобы минимизировать транспортные затраты, обеспечивая при этом допустимую нагрузку для каждого транспортного средства.
3L-CVRP обобщает две проблемы, которые сами по себе уже трудно решить практически, а именно маршрутизации транспортных средств и погрузки коробок в трехмерном пространстве, и поэтому является сложной задачей оптимизации. Проблема учитывает широкий ряд ограничений, взятых непосредственно из реальных сценариев, что связывает её с реальными грузоперевозками. Мало того, что задача оптимизации является NP-полной (Gendreau и др., 2006), она также усложнена проверкой найденного решения на то, что может ли набор трехмерных коробок быть упакован в контейнере (Martello и другие, 2000).
Будучи относительно новой проблемой высокой сложности, лишь несколько решений появляются в литературе. Gendreau и др. (2006) предложил решение, в котором обе подпроблемы: маршрутизация и загрузка, были решены с помощью независимых алгоритмов на основе поиска с запретами. de Ara'ujo (2006) достигнуты лучшие результаты с более сложным алгоритмом упаковки. А затем следовал Tarantilis и др. (2009) с поиском с запретами с управляемым локальным поиском в сочетании с несколькими быстрыми и простыми упаковочными эвристиками. Качество решения было затем усовершенствовано Fuellerer и др. (2010) с подходом оптимизации колонии муравьёв, также с быстрыми эвристиками для погрузки.
Совсем недавно опубликованные решения используют некоторую форму поиска с запретами. Tao и Wang (2010) достигают в
настоящий момент лучших результатов с наименьшей свободной упаковочной эвристикой. Wang и др. (2010) получил
аналогичные решения с тонкой настройкой в нижнем левом углу и максимально схожими эвристиками области для загрузки.
Наконец, Bortfeldt (2010) получил сопоставимые результаты с частью вычислительных усилий, другими методами
путем селективной упаковки, сгенерированного поиска окрестности пользуясь алгоритмом дерево-решений
. Iori и др. (2007) представил точный алгоритм ветвей и границ для 2l-cvrp, но, насколько нам известно, нет все еще никакого точного решения для 3L-CVRP.
В этой статье мы предлагаем алгоритм поиска с запретами с улучшенным локальным поиском 3L-CVRP. Мы обнаружили, что эффективность подпрограммы упаковки имеет решающее значение, и для этого мы опираемся на эвристики с поправкой - несколько перестановок в нижнем левом углу на 3D-пространстве. Наш основной вклад представляет собой новый смешанный алгоритм упаковки, многократные просмотры динамической матрицы представлений и усовершенствование алгоритма на основе Табу-поиска
Далее эта статья организована так: следующая секция должным образом определяет проблему, секция 3 детализирует наш предложенный алгоритм поиска с запретами, а также алгоритм упаковки. Результаты вычислений представлены в секции 4. Заключения представлены в секции 5.
2. Определение проблемы
Мы рассматриваем полный граф G = (V,E), где V = {0, 1, ..., n} должно быть задано n+1 вершиной, среди которых v0 – депо или склад и n клиентов v1,……,vn. Каждая вершина eij ∈ E между vi и vj имеет связанную стоимость с направленем - cij . Мы получаем парк v идентичных транспортных средств. Каждое ТС имеет грузоподъемность D и трехмерный контейнер с шириной W, высотой H и длинной L. ТС имеет сзади открывающуюся часть размерами H×W для загрузки и разгрузки.
Каждый клиент i имеет требования товаров mi. Каждый товар обозначается Iik, где i = 1, ..., n представляет клиента, которому товар должен быть доставлен и k = 1, ..., mi конкретизирует товар. Общий вес набора изделий mi - di. Каждый товар имеет ширину wik, высота hik и длина lik (i = 1, ..., n; k = 1, ..., mi).
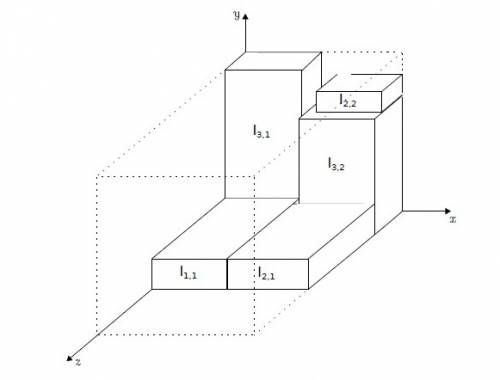
Рисунок 1 – Допустимый план упаковки
Действительный маршрут - последовательность трёх или больше узлов, начинающихся и заканчивающихся в v0, где никакой клиент не появляется более одного раза. Полная стоимость маршрута - сумма всех его составляющих вершин. Решение 3L-CVRP - представляет собой набор максимально допустимых v маршрутов таким образом, что каждый клиент посещается ровно один раз и имеется соответствующий действительный план упаковки, предусмотренный для данного маршрута. Цель - минимизировать полные транспортные расходы, связанные с маршрутом.
План упаковки является допустимым, если все следующие ограничения удовлетворены:
1. Все товары соответствующих клиентов, которые появляются в соответствующем маршруте, упакованы надлежащим образом, не перекрываются и полностью содержится в контейнере.
2. Ориентация всех коробок фиксируется относительно высоты, и они могут быть повернуты только на 90 ° горизонтально. Края ящиков должны быть параллельны сторонам контейнера.
3. Каждый товар имеет соответствующий флаг ƒik хрупкости, который установлен в единицу, если элемент iik является хрупким и ноль в противном случае. Нехрупкие предметы не могут быть размещены сверху хрупких.
4. Каждая коробка должна иметь минимальную опорную зону в контакте с его основанием. Все товары, которые не помещаются непосредственно на полу, должны иметь процент от его основания в непосредственном контакте с другими контейнерами. Это, как правило, установлено на 75%.
5. При разгрузке товаров i-го клиента, должна быть обеспечена возможность сделать это для всех его элементов, используя только движения параллельно длине транспортного средства. Это означает, что ни один товар другого клиента, который посещается позже на маршруте не может быть размещен сверху или между iik и задней частью транспортного средства при всех k = 1, ..., mi. Эта политика в последствии называется LIFO (последний вошел- первый вышел).
На рисунке 1 приведен пример допустимого плана упаковки.
3. Предложенный алгоритм
Наше решение использует тот же самый двухэтапный подход, предложенный Жендро и др. (2006), то есть, мы считаем маршрутизацию и упаковку по отдельности, каждый со своим собственным алгоритмом, который затем координируется для получения полного решения.
Сначала мы опишем структуру данных, используемую для представления грузового пространства транспортных средств. После этого мы подробно рассмотрим наш алгоритм упаковки. Затем мы представим нашу стратегию поиска с запретами, которая итеративно вызывает функцию упаковки.
3.1 Контейнерное представление
Процедура упаковки вызывается несколько раз в течение полного выполнения упаковки грузов, поэтому очень важно для неё давать хорошие результаты в соответствующее короткое время. Кроме того, мы должны убедиться, что наше представление является достаточно мощным, чтобы всякий раз, когда находится допустимое решение, мы можем сохранить его, а некорректные отбросить.
Мы достигаем этого за счет расширения динамической матрицы, предложенной Ngoi и др. (1994) с несколькими представлениями. Основной идей использования динамической матрицы, является представление транспортного средства только в двух измерениях и сделано это путем разделения его на минимальное количество ячеек. Каждая коробка затем полностью описывается в терминах ячеек, которые она занимает. Контейнер начинается только с одной ячейкой, представляющей все его свободное пространство. Когда все большие элементы будут упакованы, ячейки впоследствии можно разделить по мере необходимости.
Основной проблемой, связанной с динамической матрицей, является то, что она имеет лишь частичную информацию о третьем измерении (высота). Это означает, что пространство может быть потрачено впустую, если существует только один активный вид "сверху" в каждый момент времени. Многие из возможных планов упаковки, генерируемых алгоритмом, нельзя использовать, потому что мы не в состоянии эффективно использовать пустое пространство ниже уже упакованных коробк. Эта проблема возникает только тогла, когда коробка устанавливается с менее чем на 100% областью поддержки. Чтобы решить эту проблему, мы создаем новое представление на высоте основания каждый раз, когда ящик помещается и не полностью поддерживается, если нет уже ранее созданного представления на этой высоте. Это имеет очень малое влияние на производительность, так как ячейки и представления очень малы по отношению к обычным размерам пустот.
Это представление имеет преимущество по сравнению с более простыми в тех случаях, когда введение новой коробки расширяет зону поддержки ранее предоставленной верхней стороне другой смежной коробки. Например, на рисунке 1, I1;1 и I2;1 обеспечивают объединенную площадь поверхности, на которой может быть помещена большая коробка. Это также имеет место, даже если имеются пробелы и другие коробки между ними.
3.2 Алгоритм упаковки
Для данного маршрута процедура упаковки должна поместить все товары всех клиентов, которые посещаются в течении маршрута и удовлетворять всем ограничениям, описанным в разделе 2. Наш алгоритм использует эвристический подход подобный на тот, который используется Gendreau и др. (2006), в котором дана последовательность товаров, жадно помещенных на свободном место с минимальным z, без привязки к минимальному по х, и минимальному по у. Элемент сначала помещается одной из его сторон, параллельных сторонам контейнера, а затем поворачивается на 90 ° в х – z плоскость, если первая ориентация не подходит. Это называется 3D эвристикой нижней левой.
Алгоритм затем помещает все элементы в контейнере шириной W , высотой Н и бесконечной длины. Цель состоит в том, чтобы свести к минимуму применение длины без нарушения каких-либо ограничений. Полученный в результате план упаковки считается возможным, если она имеет длину меньше или равна L.
Важное наблюдение состоит в том, что порядок элементов значительно влияет на эвристики. Изменяя его мы можем генерировать различные планы упаковки. Имея это в виду, тестируется целый ряд различных перестановок, пока возможная упаковка не будет найдена или число итераций не достигает предела θn2, где n число элементов в последовательности.
Хорошая стартовая последовательность найдена, если мы сортируем товары в обратном порядке посещения клиентов, для того, чтобы повысить шансы генерации решений, которые будут удовлетворять ограничение на LIFO. Пусть seq0 = (1,..., n) будет этой последовательностью. Затем мы перемешиваем его, чтобы получить новую последовательность с измененными позициями. Чрезвычайно важно отметить, что данный порядок seq1 = (2, 1, 3, 4,...., n) будет более возможным (т.е. удовлетворит LIFO) с гораздо большей вероятностью, чем, например, seq2 = (n, n-1,...., 1). Принимая это во внимание, мы предлагаем вероятностный алгоритм 1 для генерации упорядочения коробок.
Алгоритм 1 – Упаковка
Ввод: список коробок для упаковки
Выход: план упаковки
1: повтор
2: для i 0 до θп2 делать
3: создать индексирование вектор idx, где idx [i] указывает на i коробку
4: для всех idx [i] делать
5: idx [i] случайным образом () // случайное целое положительное число
6: idx [i] ←idx [i]= (случайная () mod(n - i + 1))
7: idx [i] ← idx [i] = (случайная () mod(n - i + 1))
8: конец
9: сортировать idx в порядке возрастания
10: вызов 3lbottomleft эвристики с коробками в порядке, определенном соответствующим idx
11: конец
12: до тех пор, пока решение не выполнено или не улучшено
Когда мы находим допустимую упаковку для группы клиентов, мы прячем это решение до последующего вызова с теми же аргументами, что приводит к последующему поиску среди спрятанных решений. Если мы не можем найти допустимую упаковку, то мы не прекращаем алгоритм немедленно. Это связано с тем, что мы можем найти лучшую упаковку на следующем итерации алгоритма. Алгоритм работает, однако, прекращает свою работу после τ попыток, чтобы не тратить время бесцельно на невозможном или очень трудном маршруте. В этом случае решение отмечается неосуществимым и прячется про запас, чтобы избегать дальнейших попыток упаковать его.
3.3 Маршрут
Часть составления маршрута 3L-CVRP реализуется поиском с запретами. Начальное решение строится с помощью алгоритма Кларка и Райта (1964), а затем улучшается путем поиска в ее окрестности. Сберегательный алгоритм работает следующим образом. Во-первых, каждый клиент помещается в отдельный маршрут. Строится список сбережений, в котором для каждой пары клиентов (i, j) вычисляется его сбережение в качестве ci0 + c0j - cij , что соответствует уменьшению расстояния при объединении двух маршрутов с конечными точками i и j. Затем выбираем пару с наибольшим сбережением присоединенных конечных точек и итеративно объединяются в соответствующие маршруты, если существует подходящий план упаковки. Если после этого у нас есть решение маршрутизации с количеством маршрутов, большим чем v, мы снова выбираем лучшую пару и объединяем соответствующие маршруты, даже если мы не можем найти допустимую загрузку, а затем повторяем этот процесс, пока число маршрутов не равно V. В этом случае исходное решение не будет возможным.
После того, как создается начальное решение, мы продолжаем оптимизацию. Следующая процедура повторяется до тех пор, пока ограничение по времени не будет достигнуто. На каждой итерации соседние решения рассматриваются в определенном порядке. Мы всегда должны обеспечить осуществимый план упаковки для любых новых маршрутов и для этого нам нужно вызывать процедуру упаковки каждый раз, когда мы оцениваем соседа. Целевая функция вычисляется как d + αew+βeL, где d является общей длиной всех маршрутов, αew общий избыточный вес и eL общая избыточная длина.
Мы всегда принимаем любое движение без штрафов, что приводит к лучшему решению, чем текущее. Если мы не можем найти решение, мы принимаем первый шаг, который улучшает целевую функцию, или нет решения. Выбранный шаг затем применяется и добавляется в лист запрета, который всегда содержит последние шаги, которые были сделаны.
После того, как найдено первое допустимое значение, никакие неосуществимым решения не принимаются больше (мы вводим выполнимый метод). Это дает нам преимущество, так как нет необходимости в создании упаковочного плана, который увеличивает общее расстояние.
Типы движения между двумя маршрутами R0 и R1:
1. Движение изменения: вставить клиента i ∈R0 в определенном положении в R1 и удалить его из R0.
2. Движение обмена: учитывая i ∈ R0 и R1 принадлежащего 2 обменять i и j.
3. Движение пересечения: после определения точки разделения в обоих R0 и R1, R0 строится как: первая половина R0, и вторая половина R1. То же самое делается для R1.
4. Движение внутреннего обмена: обмен i ,j ∈R0.
После того, как движение принимается, каждый отдельный ход клиента, содержащийся в движении, объявляется как запрещенным для следующих итераций T (запретами владения). Например, после обмена, клиент i не может вернуться к R0 и клиент j не может вернуться к маршруту R1 во время пребывания в листе запрета. Та же идея применима ко всем другим типам движений, то есть, мы запрещаем полностью изменяющие шаги. .
Мы исследуем окрестности в следующем порядке. Во-первых, мы оцениваем все возможные перемещения для всех пар различных маршрутов. Затем мы оцениваем все ходы обмена и после этого для всех происходит движение изменения, перебирая все возможные точки вставки. Для конкретного типа перемещения все маршруты повторяются в случайном порядке. Внутренний обмен делается выборочно: мы случайным образом оцениваем niswaps ходы. Если мы находимся в оптимальном решении и уже выполнили оптимальные переходы, то мы пропускаем все последующие шаги, которые не приводят к лучшему решению относительно общей длины (нам не нужно вызывать алгоритм упаковки).
Если после того, как все ходы оценены, лучшее решение по-прежнему не найдено, но это лучшее решение по отношению к общей длине, чем у текущего лучшего решения, мы активизируем поиск плана упаковки, вызвав процедуру загрузки еще раз для всех маршрутов, которые в настоящее время имеют штрафы.
4. Вычислительные результаты
Наш алгоритм был реализован в ANSI C ++ и скомпилирован с использованием GCC с флагом оптимизации - O3. Все тесты проводились с использованием одного ядра с i7 Intel 930 с тактовой частотой 2,8 ГГц и 12 Гб оперативной памяти. Набор используемых экземпляров доступен по адресу http://www.or.deis.unibo.it/research.html и был предоставлен Жендро и др. (2006). Тесты для каждого экземпляра проводились до тех пор, пока не был достигнут предел времени. В таблице 1 приведены значения всех параметров алгоритма, используемого в вычислительном эксперименте.
Таблица 1: Параметры, используемые в вычислительном эксперименте
|
Параметр |
Описание |
Значение |
|
τ |
Попыток прежде чем сдаться |
10 |
|
θ |
Постоянная упаковочных перестановок |
30 |
|
niswaps |
Количество случайных внутренних обменов |
min(n2/4,250) |
|
T |
Табу владения (tabu tenure ) |
Min(15,n/2) |
|
α |
Штраф избыточного веса |
20δ/D, where δ = average(cij ) |
|
β |
Штраф избыточной длины |
20δ |
|
time limit |
Максимальное время табу-поиска |
900s if n < 35, 1800s if 35 ≤ n < 50, 3600s otherwise |
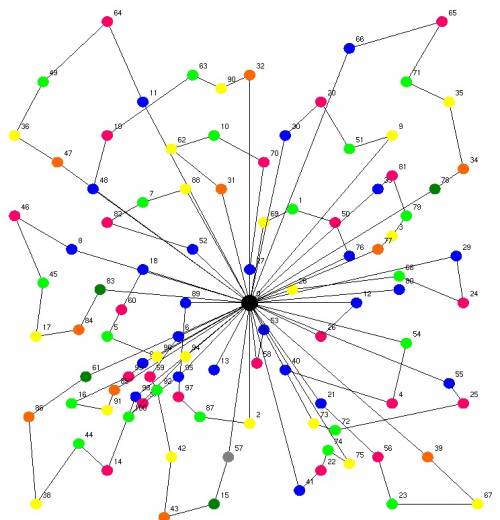
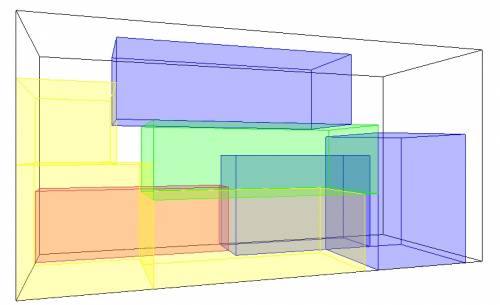
Рисунок 2: Маршрутизация (а) и упаковки (б) для примера с 26 экземплярами.
В таблице 3 представлены результаты, полученные при выполнении данного алгоритма со всеми ограничениями, налагаемыми на нагрузки. Каждое решение является осуществимым. Каждый экземпляр идентифицируется своим индексом i вместе с числом клиентов n и общим количеством коробок м, которое он содержит.
Все результаты представлены как среднее общее пройденное расстояние после десяти выполнений того же метода. Для всех методов, которые мы представляем средний (ttdavg) и лучший (ttdmin) результаты поиска были найдены после десяти опытов с различными случайными источниками, за исключением Тао и Ван (2010), для которого только средний результат был найден. Наиболее лучшие значения для каждой сущности выделены жирным шрифтом везде, где они появляются. Время выполнения приведено в секундах и соответствуют среднему времени, затраченному алгоритмом для достижения наилучшего решения, за исключением Bortfeldt (2010), он представляет среднее общее время работы алгоритма. Кроме того, мы предоставляем среднее значение для всех столбцов. Для сравнения, мы показываем разрыв между нашими результатами и результатами из литературы, что соответствует средней процентной разнице во всех случаях. Положительный разрыв указывает на то, что наши результаты, в среднем, лучше. Процессор, используемый каждым методом в том же порядке, как они представлены в таблице 2: Pentium IV 3,2 ГГц, Intel Xeon E5430 2,66 ГГц, Pentium IV 2.39GHz, Core 2 Duo E8500 3.17GHz и Core i7 930 2.8GHz. На рисунке 2 приведен пример маршрутизации и упаковки, полученной нашим методом для примера с 26 сущностями.
Результаты показывают, что наш метод способен находить хорошие решения. В среднем, наш алгоритм демонстрирует лучшие результаты, чем все остальные, улучшение общего пройденного пути находится в пределах от 0,4% до 1,87%. По причине ограниченного пространства, мы опустили результаты Gendreau и др. (2006) и Tarantilis и др. (2009). Мы отмечаем, что средний разрыв по отношению к их решениям составляет 8,16% и 4,79%, соответственно. В таблице 2 приведено сравнение числа раз которое каждый метод нашел наилучшее минимальное значение и наилучшее среднее значение. Мы можем видеть, что в отношении качества решения наш метод превосходит всех остальных, за исключением Bortfeldt (2010), который способен найти еще одно минимальное решение. С другой стороны, мы превосходим его в среднем, поскольку он получил только шесть средних лучших решений, а средний разрыв по-прежнему 1,29% по сравнению с нашим методом. Кроме того, мы видим, что наш алгоритм особенно хорош в большинстве случаях с 50 или более клиентов, для которых мы получаем 6 новых лучших значений из 9-ти экземпляров. Что касается вычислительных усилий, наш алгоритм сравним со всеми другими методами, за исключением, Bortfeldt (2010), который занимает значительно меньше времени в подобной установке.
Таблица 2: Сравнение числа лучших решений, полученных с помощью методов из литературы.
|
|
Fuellerer et al. (2009) |
Wang et al (2010) |
Tao and Wang (2010) |
Bortfeldt(2010) |
Our method |
|
Best minimum |
2 |
9 |
- |
13 |
12 |
|
Best average |
2 |
4 |
8 |
6 |
12 |
Таблица 3: Производительность нашего алгоритма по сравнению с результатами из литературы.

Выводы
3L-CVRP является интересной и сложной проблемой, это связано как с ее теоретической сложностью, так и с ее прямым отношением к реальным приложениям. В данной работе мы представили решение на основе алгоритмов маршрутизации поиска с запретами и новой эвристикой упаковкой. Мы обнаружили, что упаковка чрезвычайно важна для получения хороших конечных результатов, и предлагаемый вероятностный алгоритм упаковки и представление 3D грузового пространства в значительной степени ответственны за качество наших решений. Через вычислительные эксперименты нам удалось показать, что наш метод получает равнозначные или лучшие результаты, чем те, что представлены ранее в литературе. Наш метод является устойчивым в том смысле, что в среднем он доминирует над всеми другими методами и получает лучшие результаты для крупных экземпляров.
Список использованной литературы:
- Baker, B.S., Coffman Jr., E.G. and Rivest, R.L. (1980). Orthogonal packing in two dimensions, SIAM Journal on Computing 9: 846-855.
- Bortfeldt, A. (2010). A Hybrid Algorithm for the Capacitated Vehicle Routing Problem with ThreeDimensional Loading Constraints, Diskussionsbeitrage der Fakult ВЁ at f ВЁ ur Wirtschaftswissenschaft ВЁ der FernUniversitat in Hagen ВЁ 460.
- Clarke, G. and Wright, J. (1964). Scheduling of vehicles from a central depot to a number of delivery points, Operations Research 12: 568-581.
- de Araujo, O. C. B. (2006). Вґ Problemas de Corte e Empacotamento Tridimensional e Integraccom Roteamento de Veiculos, PhD thesis, Faculdade de Engenharia Eletrica e de Computacao - UNICAMP, Campinas, Brasil.
- Fuellerer, G., Doerner, K.F., Hartl, R. and Iori, M. (2010). Metaheuristics for vehicle routing problems with three-dimensional loading constraints, Eur J Oper Res 201: 751-759.
- Gendreau, M., Iori, M., Laporte, G. and Martello, S. (2006). A tabu search algorithm for a routing and container loading problem, Transportation Science 40(3): 342-350.
- Iori, M., Salazar Gonzalez. J.J. and Vigo, D. (2007). An exact approach for the symmetric capacitated vehicle routing problem with two dimensional loading constraints, Transportation Science 41(2): 253-264.
- Martello, S., Pisinger, D. and Vigo, D.. (2000). The three-dimensional bin packing problem, Operations Research 48: 256-267.
- Ngoi, B. K. A., Tay, M. and Chua, E. (1994). Applying spatial representation techniques to the container packing problem, International Journal of Production Research 32: 111-123.
- Portal, G., Rocco, R., Ritt, M. and Buriol, L.S. (2009) Uma busca tabu aplicada ao problema de roteamento com restricВёoes de empacotamento tridimensionais, Anais do XLI Simposio Brasileiro Вґ de Pesquisa Operacional.
- Tao, Y. and Wang, F. (2010). A new packing heuristic based algorithm for Vehicle Routing Problem with Three-dimensional Loading constraints, IEEE Conference on Automation Science and Engineering (CASE), pp. 972-977.
- Tarantilis, C.D., Zachariadis, E.E. and Kiranoudis, C.T. (2009). A hybrid metaheuristic algorithm for the integrated vehicle routing and threedimensional container-loading problem, IEEE Transactions on Intelligent Transportation Systems 10: 255-271.
- Toth, P. and Vigo, D. (2002). The Vehicle Routing Problem, SIAM Monographs on Discrete Mathematics and Applications, Philadelphia, PA.
- Wang, L., Guo, S., Chen, S., Zhu, W. and Lim, A. (2010). Two Natural Heuristics for 3D Packing with Practical Loading Constraints, PRICAI 2010: Trends in Artificial Intelligence, pp. 256-267.