ИНТЕРВАЛЬНЫЙ АНАЛИЗ И ЕГО ПРИМЕНЕНИЕ ПРИ РАСЧЕТАХ ПАРАМЕТРОВ СЕРВЕРНЫХ КОМПЬЮТЕРНЫХ СИСТЕМ

Рассмотрены основные свойстваинтервалов и операций над ними с целью демонстрации преимуществ использования интервальных типов данных в качестве входных и результирующих параметров, а также использование интервального анализа как основного инструментария при реализации комплексных расчетов параметров серверных компьютерных систем. Показаны пути перехода от традиционного представления сетевых параметров к интервальному. Приведена демонстрация применения интервальных вычислительных методов напримере расчета времени откликасистемы обработки запросов.

Ключевые слова: интервал, интервальный анализ, погрешность, время отклика.

ВВЕДЕНИЕ

В настоящее время кинтервальномуанализу (предметом которого является решение задач с интервальными неопределенностямии неоднозначностямив данных [1, 2]) как к средству представления и обработки факторов неопределенности обращено пристальное внимание инженеров и конструкторов, как к наиболее адекватному описанию начальных условийприпрактической постановкеинженерных задач. В качестве основных параметров интервальногоанализавыступает неопределенность (также называемая интервальной), указывающая только границывозможных значенийнекоторойвеличины (либопределы ее изменения), знания о которой являются неполными (или частичными). Интервальная неопределенность величины, выраженнаянеким интервальным параметром (или просто интервалом), имеет ряд особенностей: любая величина, имеющаяинтервальную неопределенность, можетбыть представленатолькопределамиееизменения (границами возможных значений); естественной мерой неопределенности (неоднозначности) такой величиныявляется ширина интервала, определяющая диапазон «захвата» значенийна числовом множестве; интервал также является результатом арифметических операций над интервальными параметрами.

В контексте интервального анализа интервал [a, b] представляет числовые промежутки в качестве основного объекта данных и не содержит никакой дополнительной информации о самой величине. Поэтому интервал [a, b] трактуется как множество возможных значений неизвестной истинной величины в пределах значений a ? b числовой оси.

Возникновение неопределенностей и неоднозначностей в данных при реализации комплексных расчетов параметров серверных компьютерных систем является тем фактором, который оправдывает использование методов и средств интервального анализа при разработке усовершенствованных способов расчета основных параметров серверных вычислительных систем и сетей, позволяющих повысить эффективность использования серверных компьютерных ресурсов.

Целью данной работы является реализация различных модулей для расчета параметров серверных компьютерных систем с помощью средств интервального анализа. При этом за основу взяты наиболее важные зависимости, учет которых может потребоваться при расчете параметров серверных компьютерных систем

ОСНОВНЫЕ ОСОБЕННОСТИ ИНТЕРВАЛЬНОЙ АРИФМЕТИКИ

Актуальность применения интервальной арифметики заключается, прежде всего, в ее применении при реализации компьютерных вычислений [3]. В частности, внешне приближенные значения интервальной арифметики позволяют выразить диапазон полученных результатов при использовании интервальных операций и функций. Это дает качественные различия в научных расчетах по отношению к традиционным вычислениям (в которых используются данные без учета ошибок округления), так как полученный результат в виде интервала (набора значений) гарантированно содержит истинный (правильный, точный) результат внутри его крайних значений (границ интервала). В данном разделе описаны все необходимые свойства и методы работы с интервалами, применение которых являетсянеобходимым «стартовым» набором для успешного применения интервальных вычислений при расчетах параметров серверных компьютерных систем.

Так, для пары интервальных значений х = [ , ]x x и y = [ , ]y y в интервальном анализе определены четыребазовыеарифметических операции «op» (от англ. operation): х op y = {х op y | х ? х ? y ? y} для op ? {+, –, ?,?}. (1)

Множество всехинтервальных значений (интервалов) обозначается через I(R), поэтому х, y?I(R).

Таким образом, результатом каждой из четырех основных операций «op» является интервал, значения которого, соответствуют точному диапазону каждого набора значений из областей интервалов-операндов при выполнении над ними определенной в «op» операции [4]. Хотя запись (1) характеризует эти операции согласно математической нотации, можно рассмотреть каждую операцию в отдельности, например

Заметим, что операцию вычитания (3) можно реали- зовать через операции умножения (4) и сложения (1):

–y = (–1) y = [–1, –1] ?yи х – y = х +(– y).

Кроме арифметических операций, для интервалов справедливы операции теоретико-множественного аппарата [5]:

1) равенство интервалов: х = y тогда и только тогда, когда выполняется условие x = y ? x = y;

2) сравнение интервалов: х > y (х < y) тогда и только тогда, когда выполняется условие x > y (x < y);

3) включение интервалов: х? y (х ? y) тогда и только тогда, когда выполняется условие x < ? < y x y.;

4) принадлежность интервалов х ? y расширяет условия строгого включения (п. 3), допуская равенство интервалов (х? y ? х=y ? х?y, т. е. x ? ? ?y x y );

5) пересечение интервалов х?y=? (пусто), если х < y ?х > y, в противном случае х? y = =[max( , ), min( , )]x y x y ;

6) объединение интервалов: х?y= =[min( , ), max( , )].x y x y

Из определения (1) видно, что интервальные операции сложения и умножения обладают свойствами коммутативности и ассоциативности, т. е. длях, y, z? I(R) имеют место равенства:

–y = (–1) y = [–1, –1] ?yи х – y = х +(– y).х + y = y + х, (х + y) + z = х + (y+ z),

–y = (–1) y = [–1, –1] ?yи х – y = х +(– y).х ?y = y ?х, (х ?y) ? z = х ? (y ? z).

Закон дистрибутивности для интервально-арифметических операций не всегда имеет место, однако всегда справедливо включение:

Соотношение (7) называют субдистрибутивностью интервальных операций сложения и умножения.

Использование интервальных значений в расчетных модулях серверных компьютерных систем предполагает учитывать ряд параметров, которые описывают «метрические показатели» интервалов:

1) ширина wинтервала x определена равенством:

2) середина m интервала x является полусуммой его границ:

3) абсолютная величина интервала |x| определяется как

На множестве I(R) имеют место так называемые вырожденные (или точечные) интервалы, которые отождествимы с вещественными числами множества R. У вырожденногоинтерваласовпадают границы, т. е. x = x x= , где х – вещественное число. Поэтомусправедливо соотношение множеств действительных и интервальных чисел: R?I(R), откуда следует, что любое действительное число также можно выразить в виде точечного интервального значения.

Вырожденные интервалы [0, 0] и [1, 1] играют роль обычных нуля и единицы. Другими словами,

х + 0 = 0 + х = х, х ? 1 = 1 ? х = х

для любого х ? I(R).

Равенство (1) (как, впрочем, и (2–6)) показывает, что если один из операндов является невырожденным интервалом, то и результат арифметической операции также невырожденныйинтервал (исключение составляет умножениена 0 = [0, 0]). Отсюда, в частности, следует, что для невырожденногоинтервала хвычитаниене обратно сложению, деление не обратно умножению. Значит,

х – х ? 0 , х / х ? 1

при w(x) > 0. Однако всегда справедливо включение

0?х – х , 1? х / х

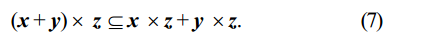
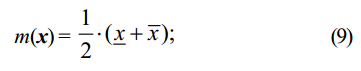
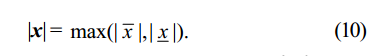
ИСПОЛЬЗОВАНИЕ МЕТОДОВ ИНТЕРВАЛЬНОГО АНАЛИЗА В РАСЧЕТНЫХ МОДУЛЯХ СЕРВЕРНЫХ КОМПЬЮТЕРНЫХ СИСТЕМ

Расчетные модули, реализующие основные зависимости, характерные для серверных компьютерных систем по типу сложности можно разделить на две основные группы. Первая группа – относительно простые модули, позволяющие анализировать и рассчитывать отдельные серверные параметры на основе базовых законов и закономерностей (закон для времени отклика, закон Литтла, закон потребности в обслуживании и др. [6]). Вторая группа – модули, позволяющие выполнять более сложные и комплексные расчеты для различных серверных подсистем и серверных комплексов [7].

На начальном этапе использования интервального анализа в расчетных модулях для серверных компьютерных систем необходима адаптация упомянутых в предыдущем абзаце базовых законов и закономерностей. Такая адаптация заключается, прежде всего, в том, чтобы в расчетах использовать не усредненные точечные значения исходных параметров, а интервальные, учитывающие отклонения (колебания) значений этих параметров, вызванные целым набором различных факторов. Это может быть, например, нестабильность физической среды передачи данных, неравномерность распределения сетевых ресурсов, мгновенно изменяющаяся нагрузка на аппаратные и программные компоненты серверных систем и т. п.

Таким образом, возможны два пути перехода от традиционного представлениявходных параметров кинтервальному:

1. Входной параметр а может быть определен как интервальный а = [ , ]a a , предельные значения которого выражаются как

где ?а – предельное отклонение от усредненного значения параметра a (значения, которое использовалось бы при традиционных расчетах). Учитывая (9), очевидно, что a = m(а). При этом ?а фактически является абсолютной погрешностью а, которая может выбираться в зависимости от факторов, влияющих на достоверность получения численного значения входного параметра (это могут быть инструментальные (приборные), методические и (в меньшей степени) субъективные (операторные, личностные) погрешности [8]). Очевидно, что w(a) = 2?а.

2. Входной параметр а может быть определен как интервальный а = [аmin, amax], предельные значения которого аmin и amax могут быть получены как минимальное и максимальное значение из выборки (или группы выборок) величины а. При этом из статистических соображений рекомендуется, чтобы число случаев, включенных в выборочную совокупность (объем выборки) было не менее 30–35 [9].

В качестве примера можно рассмотреть один из действующих законов в клиент-серверных системах –закон времени отклика (response time law) [6, стр. 107], который выражается следующим соотношением:

где r – искомое среднее время отклика рассматриваемой системы обработки запросов; k – количество источников запросов (например, клиентские рабочие станции или приложения, посылающие запросы), поступающих в рассматриваемую систему; х0 – пропускная способность системы обработки запросов; z – время обдумывания пользователем (среднее время, проходящее междуполучением пользователем ответа на свой запрос и отправкой нового запроса от одного и того же источника).

На начальном этапе осуществляется переход кинтервальным типам данных. Поскольку значение z является усредненным (по определению), целесообразно вместо него использовать интервал z. Пропускную способность системы обработки запросов также можно задать интервалом х. Тогда интервал r будет искомым временем отклика рассматриваемой системы обработки запросов, включающий в себя все возможные значения времени отклика (в том числе и среднее время отклика), которые зависят от множеств z и х. Количество источников запросов kконкретно и его целесообразно (но необязательно) представлять в виде точечного (конечного) значения – целого числа.

Пусть z = 10 сек., х0 = 8 запросов/сек. Тогда примем следующие допущения: Dz = 2 сек. и Dх=3 запросов/сек. (учитывая что z – Dz > 0 и x0 – Dх > 0). Тогда, согласно (11), получаем

z = [z , z] = [z - ?, z + ?] = [8,12](сек.),

x = [x , x] = [x - ?, x + ?] = [5,11](запросов/сек).

В табл. 1 показаны результаты расчета времени отклика рассматриваемой системы обработки запросов (12) с использованием средств традиционных и интервальных вычислений (учитывая, что значение времени положительное число: r > 0 и r > 0) при различных количествах источников запросов.

На рис. 1 показаны результаты расчета времени отклика как для точечных, так и для интервальных значений. Темная область на графике – диапазон возможных значений времени отклика в зависимости от количества источников запросов.

ЗАКЛЮЧЕНИЕ

Таким образом, в работе были рассмотрены основные концепции использования средств и методов интервального анализа при реализации комплексных расчетов параметров серверных компьютерных систем. При расчете временных параметров сетевой инфраструктуры использование средств интервального анализа позволяет оперировать точными значениями входных параметров (при традиционных вычислениях используются усредненные значения). Полученный при этом диапазон результирующих значений позволяет провести более качественную оценкуэффективности работы серверных компьютерных систем.

СПИСОК ЛИТЕРАТУРЫ

1. Hyvonen, E. Constraint reasoning based on interval Arithmetic: the tolerance propagation approach / E. Hyvonen. – Artificial Intelligence. – v. 58. – 1992. – 412 p.
2. Интервальный анализ и его приложения. Краткий неформальный очерк. [Электронный ресурс] – Режим доступа: http://www.nsc.ru/interval/index.php.
3. Аноприенко, А. Я. Интервальные вычисления и перспективы их развития в контексте кодо-логической эволюции / А. Я. Аноприенко, С. В. Иваница // Научные труды Донецкого национального технического университета. Серия «Проблемы моделирования и автоматизации проектирования динамических систем» (МАП-2010). – Вып. 8 (168) : Донецк : ДонНТУ. – 2010. – С. 150–160.
4. Kearfott, R. B. Interval computations: introduction, uses and resources. Department of Mathematics University of Southwestern Louisiana / R.B. Kearfott– USL Box 4–1010, Lafayette, LA 7054–1010. – USA. [Электронный ресурс]. – Режим доступа: http://www.nsc.ru/interval/Introduction/BakerSurvey.pdf.
5. Калмыков, С. А . Методы интервального анализа / С. А. Калмыков, Ю. И. Шокин, З. Х. Юлдашев. – Новосибирск : Наука, 1986. – 224 c.
6. Менаске, Д. Производительность Web-служб. Анализ, оценка и планирование / Д. Менаске, В. Алмейда пер. с англ. – С.Пб. : ООО «ДиаСофтЮП», 2003. – 480 с.
7. Аль-Абабнех, Х. Способы и инструменты расчета параметров серверных компьютерных систем / Х. Аль-Абабнех, А. Я. Аноприенко // Информационные управляющие системы и компьютерный мониторинг – 2011 : материалы II международной научно-технической конференции студентов, аспирантов и молодых ученых (11–13 апреля 2011 года). – Донецк, ДонНТУ. – 2011. – T.3. – 301 c.
8. Назаров, Н. Г. Метрология. Основные понятия и математические модели / Н. Г. Назаров. – М. : Высшая школа, 2002. – 348 с.
9. Якушев, А. И. Взаимозаменяемость,стандартизация и технические измерения: учебник для вузов / А. И. Якушев, Л. Н. Воронов, Н. М. Федотов 6-е изд., перераб. и доп. – М. : Машиностроение, 1987. – 352 с.