Аннотация
Наталия Лаззати. Математика для экономики (Часть I).Примечание 9: Параметрической оптимизации — Огибающая теорема. Рассмотрены параметрические оптимизации, огибающая теорема. Проработаны задачи безусловной оптимизации.
Параметризованная Оптимизация в экономике
Большая часть экономического анализа рассматриваются целые семейства задач оптимизации, а не по отдельности. Рассмотрим простую модель одной переменной выбора с одним параметром.

где α∈R++ и x∈R++. Для любой спецификации это стандартная нелинейная задача программирования. В частности, поскольку ограничение установлено, она влечет за собой неравенство, это проблема Куна-Таккера. Задача (1) отличается от тех, что в примечании 8, в том, что теперь оба максимизатора х и максимальное значение целевой функции f (x*) = ln x* будет зависеть от величины α. Для этого семейства параметризованных задач оптимизации есть два вопроса которые имеют фундаментальное отношение:
- Как зависит максимальное значение целевой функции от α?
- Как зависит максимизатор от α?
Мы начнем отвечать на задачу (1), а затем расширим идею на более общие случаи.
Для любого α∈R++ и x∈R++ все точки удовлетворяют NDCQ.
Функция Лагранжа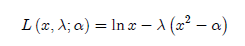
где мы разделим переменные выбора х и λ от параметра α с помощью запятой.
Так как f является C1 нестационарным (см. следствие 3 в примечании 8) необходимые условия первого порядка являются
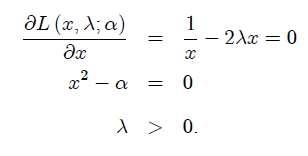
Затем

Как мы и ожидали, все эти функции зависят от α. Более того,
Это рода заявления экономистов небезосновательны. Далее мы обеспечиваем общие рамки для решения этих вопросов.
Пусть х = (x1, x2, ..., хn) от выбора переменных и α = (α1,α2,…,αl) будут вектором всех параметров, входящих в наши модели. Мы разрешим как объективно, так и ограничено функции зависить от α и соответственно будем записывать значения этих функций, как f(x;α) и U(α). Параметры должны принадлежать некоторому набору Ω который называется — допустимый набор параметров.
Рассмотрим общее семейство задач

Где α∈Ω⊆Rl и x∈X⊆Rn. Мы предполагаем Ω как и X являются открытыми множествами.
Множество максимайзеров описывается правилом решения.

То есть, S(α) есть множество элементов x* которые являются оптимальными решениями задачи (F.P) для данного α∈Ω. Если решение (F.P) является уникальным для каждого значения α, то правило принятия решения становится функцией, и мы пишем x*= x*(α).
Отдача определяется к нарастающему оптимизирующему агенту значением функции, V:Ω→R.
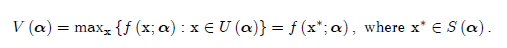
Как мы заметили ранее, в большинстве экономических приложений мы заинтересованы в утверждении, как максимальное значение функции зависит от изменений параметров, в сравнительной статики принятия решений S(α). То есть, мы хотели бы узнать, как максимальный выигрыш и поведение агента изменяется в ответ на изменения окружающей среды (например, цены, доход и т.д.). Следующий раздел отвечает на первый вопрос, а последний фокусируется на втором вопросе.
Огибающая теорема
В данном разделе рассматриваются две версии задачи (F.P), которые различаются по отношению ко множеству ограничений, и обсуждаются соответствующие теоремы, которые изучают влияние изменения α на функцию V(α). Такая теорема называется — теорема об огибающей.
Начнем с огибающей теоремы для задач безусловной оптимизации.
Теорема 1. (Огибающая теорема для безусловной оптимизации) Рассмотрим задачу (F.P) с U(α) = Rn, и пусть f(x;α) является функцией C1 пусть x*(α) является решением этой проблемы. Пусть x*(α) является C1 функцией α. Затем
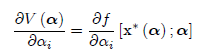
где i=1,…,l.
Доказательство. С помощью цепного правила
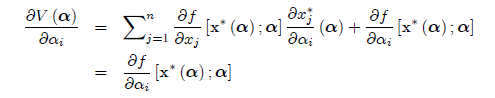
так как

обычными условиями первого порядка. В задаче (F.R) каждый параметр αi влияет на максимальную функцию значения в двух направлениях. В прямом пути, αi, влияет на V(α), потому что она является частью целевой функции f(s;α). Косвенно αi влияет V(α) через его переменных выбора x*(α); Огибающая теорема утверждает, что из утверждения ∂V/∂αi нам нужно рассмотреть только прямое воздействие αi в f(x;α), ∂f/∂αi, и оценить эту частную производную по оптимальной x*(α)!
Теорема 2. (Огибающая теорема для задачи Лагранжа) Рассмотрим задачу (F.P) с
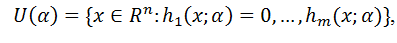
и предположим что f(x;α) является функцией C1. Пусть x*(α) является решением этой проблемы. Пусть x*(α) и множители Лагранжа μ*(α) являются функции C1 и что NDCQ содержит α. Затем
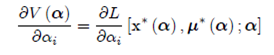
Где i=1,…,l, L является естественной функцией Лагранжа этой задачи.
Доказательство. Форма Лагранжа для задачи максимизации.
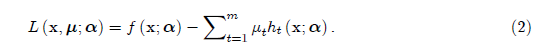
Из условий первого порядка мы знаем, что

Частной производной функции Лагранжа относительно αi в [x*(α), μ*(α); α].
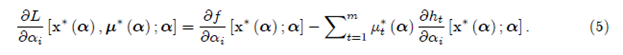
Нам нужно показать, что производная от максимального значения функции по отношению к αi равно последнему выражению.
Продифференцируем V(α), по отношению к αi
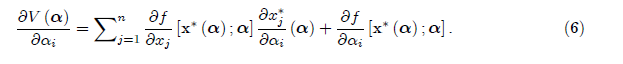
Затем вернемся к первому условию задачи и изменим условия
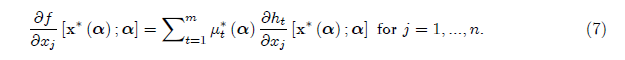
Подставляя формулу (7) в фомулу (6) и реорганизуя ее мы получаем

Последняя хитрость заключается в том, чтобы вернуться к условиям первого порядка и дифференцировать (4) относительно αi
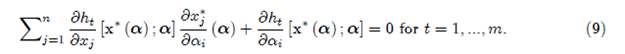
Подставляя (9) в (8), мы получаем
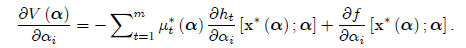
который идентичен выражению (5).
Последняя теорема является чрезвычайно важной в экономике. Это позволяет, например, обеспечить хорошую интерпретацию множителей Лагранжа.
Список использованной литературы
основанно на de la Fuente (2000, гл. 7), Madden (1986, гл. 8) и Simon и Blume (1994, гл. 19).