Решение оптимизационных экономических задач на основе генетических алгоритмов

Аннотация

Курейчик В.В., Н.В. Курейчик. Решение оптимизационных экономических задач на основе генетических алгоритмов Рассмотренны основные требования оптимизации экономических задачах, а также базовый генетический алгоритм для решения экономических задач.

Общая постановка проблемы

В последнее время наблюдается неуклонное использование математических методов в экономике. Для построения математичех моделей (ММ) экономических задач эффективно используется теории графов, а для разработок эвристических алгоритмов — методы и модели исследования операций. Одной из важнейших экономических задач является транспортная задача (ТЗ). Ее постановка следующая: задано некоторое множество товаров T={T₁, T₂,… T_n}, |T_n|=n, расположенное в различных местах M={M₁M₂,… T_p}, |M|=n. Товар должен быть перевезен в другие пункты П={П₁,П₂,… П_q}, |П|=q. При этом заданна матрица стоимости перевозок, определяющая стоимость каждой перевозки М_i П_q. Необходимо построить оптимальный план перевозки, при котором транспортные расходы минимальны в смысле заданной целевой функции.

Отметим, что практически все экономические задачи являються задачами оптимизации, в которых необходимо найти найлучшее решение. Такие задачи можно описать на основе кортежа длина три <P, D, F> гдех решений P множество решений данной задачи, D множество ограничений, позволяющее сузить множество P и выделить в нем область допостимых решений P_доп , таких что P_доп ⊆ P, F — целевая функция или критерий оптимизации.

Основные требования оптимизации:

F(P) → экстремуму (максисмуму или минимуму). Тогда решение P_i^* ∈ P_доп удовлетворяющее требованию оптимизации, и является оптимальным решением.

Существуют конктретные модификации ТЗ [1].

Это задача Монжа, когда на заднной площади размещено множество масс товаров, которые необходимо перевезти на другую заданную площадь с минимизацией транспортных расходов [2].

Это задача Ордена, когда распределение товара задно и в некоторых местах спрос превышает предложение, а в некоторых наоборот. При этом заданы стоимовти перевозок еденицы продукта. Необходио при минимальных затратах удовлетврить запрос [2].

Это задача Хичкока, когда заданы m портов отправления и n портов назначения, количество товаров, необходимых в разных портах назначения. Задача найти план перевозок с минимальными издержками [2].

С ТЗ тесно связаны задачи об оптимальном назначении, задачи о складах, задачи построения экономических моделей, промышленных взаимосвязей и др.

В отличие от существующи эвристик или влгоритмов полного перебора для поиска оптимальных решений предлагается использовать эволюционные стратегии, основаные на моделировании эволюции и алгоритмах генетического поиска.

Генетические алгоритмы это поисковые алгоритмы, основанные на механизмах натуральной селекции и генетики. Они реализуют «выживание сильнейших» среди рассмотренных структур решений, формируя и изменяя поисковый алгоритм на основе моделирования эволюции. Центральная тема поиска в генетических алгоритмах (ГА) это поиск баланса между эффективностью и качеством для «выживания», т.е. получения оптимальных решений в различных услловиях, что как нельзя лучше подходит для приведенных экономических задач.

Базовый ГА для решения сформулированных экономических задач можно укрупненно сформулировать следующие задчи:

1. Конструируется начальная популяция (набор решений заданной транспортной задчи).
2. Формируется целевая функция и производится оценка всех решений.
3. Производится селекция популяции на основе целевой функции (ЦФ). Вычисляется максимальное, минимальное, среднее значение ЦФ.
4. Члены популяции, у которых значения ЦФ выше и равно среднему значению, копируются для продолжения генетического поиска.
5. Создается набор пар из отмеченного множества решений.
6. К каждой паре применяется генетический оператор кроссинговера. В результате получается новые решения-потомки.
7. Производится подсчет значений ЦФ для новых решений.
8. Новые решения с высоким значения ЦФ вытесняют старые решения из популяции таким образом, чтобы размер ее оставался постоянным.
9. К лучшим решениям-потомкам применяются операторы мутации, инверсии, транслокации. Если в новых решениях значение ЦФ улучшается , то переход к 8, если нет, то проверяется, проведено ли данное число генераций; если да, то переход к 10, если нет, то переход к 4.
10. Конец работы алгоритма.

Данный алгоритм представляет собой модель процесса, протекающего в природе. Природа за огромное число поколений эволюции отработало оптимальные процедуры передачи наследственной информации и реализации ЦФ «выживания сильнейших». Поэтому применение генетического оператора кроссинговера, мутации, инверсии, транслокации, которые моделируют аналогичные процессы из генетики, позволяет перераспределить генетический материал и находить наилучшие решения там, где другие методы оптимизации не могут это сделать.

Пусть задано а_j — число кдкниц груза в А_i, пункте отправления i=1,2,...,n, b_j — число едениц груза, требуемого в B_j пункте назначения j=1,2,...,m. Пусть Х_ij число едениц груза, отправляемого из A_i в B_j.

Пусть

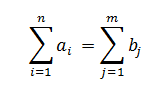
Введенем следующие ограничения

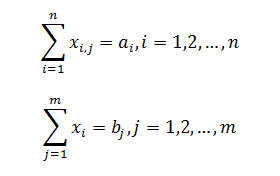
Тогда целевая функция ТЗ:

В отличие от других оптимизационных эвристик ГА, как правило, анализируют различные области простанства регений одновременно и более приспособлены к нахождению новых областей лучшим значением ЦФ, т.е. с лучшим решением за счет объедениния квазиоптимальных решенией из разных популяций.

Временная сложность ГА лежит в пределах O(on₂)–O(βn₄), где α, β — коэффициент, n — число входа алгоритма.

ГА — это мощная новая стратегия решения экономических задач большой размерности с получением оптимальных или квазиоптимальных решений.

Список использованной литературы

1. Исследование операций в 2-х томах. Том 1. Методические основы и математические методы. М.:Мир, 1981.
2. Применение в экономике теории графов. М.:Прогресс, 1966.
3. Handbook of Genetic Algorithms. Ed L.Davis, Van Nostrand Reinhold, 1991.
4. Курейчик В.М. генетические алгоритмы. Монография. Изд-во ТРТУ, Таганрог, 1998.