РАЗРАБОТКА УСТРОЙСТВА ПОИСКА ПЕРЕСЕЧЕНИЯ ЛУЧА С ПОЛИГОНАЛЬНЫМ ОБЪЕКТОМ

А.Н. Попова (5 курс, каф. КИ), А.В. Селинова (6 курс, каф. КИ),
Р.В. Мальчева, к.т.н., доцент

Целью работы является разработка вариантов параллельной реализации алгоритма поиска пересечения луча с полигональным объектом для метода обратной трассировки лучей.

Компьютерная графика широко используется в различных сферах деятельности, окружая нас ежедневно. При этом в процессе визуализации возникает проблема выбора: быстрая визуализация с потерей качества изображения или получение более реалистичного изображения с потерей времени на реализацию [1]. Метод трассировки лучей позволяет реализовывать более сложные визуальные эффекты (взаимное затемнение объектов, множественные отражения и т.д.), что делает изображения более реалистичными.

В последние годы появились аппаратные трассировщики лучей. Так NVIDIA [2] представила интерактивную систему трассировки лучей в режиме реального времени, которая использует возможности GPU. NVIDIA OptiX является программируемым конвейером, который позволяет разработчикам легко достигать нового уровня реалистичности в своих приложениях с помощью привычного языка программирования C. Используя мощь графических процессоров NVIDIA Quadro, система OptiX ускоряет трассировку лучей в широком спектре областей: автомобильное моделирование, акустический расчет, эмуляция оптики, объемные расчеты и исследование излучения. Разработчики приложений используют систему OptiX, чтобы кардинально изменить возможности дизайнеров, инженеров и исследователей. То, что раньше занимало минуты, теперь выполняется за миллисекунды, позволяя дизайнерам интерактивно экспериментировать со светом, отражениями, преломлением и тенями в реальном времени, посредством привычного программного обеспечения.

Таким образом, метод трассировки лучей продолжает свое развитие, состоящее не только в улучшении алгоритмических решений, но и их аппаратной реализации для более быстрой обработки больших объемов данных [3].

Рассмотрим математические выражения для поиска пересечения луча с полигональным объектом. Луч задан параметрическим уравнением (1). Каждая грань объекта – массивами координат вершин {x[n], y[n], z[n]} и нормальным вектором N={nx , ny, nz }, заданными в системе координат объекта (СКО).

где – координата начала луча в СКО;

– параметры луча (вектора) в СКО.

Параметр t определяет пересечение луча с многогранником и определяется отношением (2) числителя (dev) к знаменателю (div), взятому с обратным знаком.

Знаменатель представляет собой скалярное произведение вектора луча на нормальный вектор грани (выражение 3).

Числитель есть подстановка точки начала луча в уравнение плоскости грани (5). При этом свободный член уравнения плоскости, d, определяется из выражения (4) подстановкой координат любой вершины грани в уравнение.

Анализ выражений (3)–(5) показывает, что элементарный вычислительный блок (EBL) должен реализовывать умножение (рис.1).

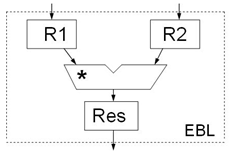
Рисунок 1 – Функциональная организация EBL

Реализация выражения (3) требует 3–х умножений и 2–х сложений (рис.2). Обозначим такой блок P0BL.

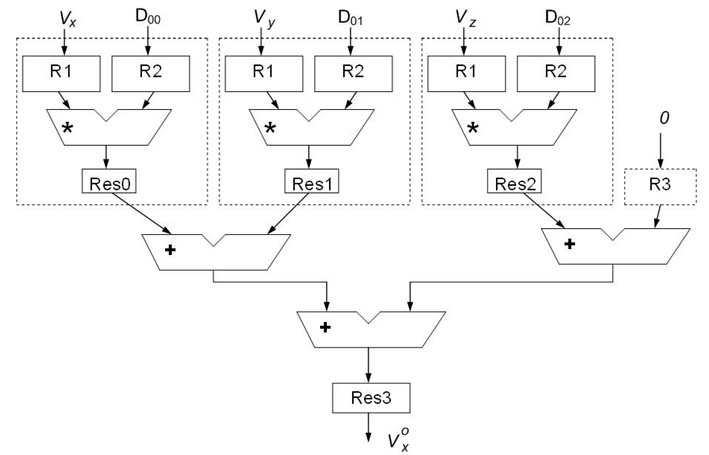
Рисунок 2 – Функциональная организация блока вычисления скалярного произведения

Блок вычисления числителя имеет ту же организацию, но в регистр R3 необходимо подать значение d. Обозначим такой блок P1BL. Блок вычисления параметра d (4) имеет такую же организацию, но дополнительно требует инверсии знака результата.

Анализируя выражения (3)–(5), стоит отметить, что делимое и делитель независимы и, следовательно, могут вычисляться параллельно. При этом для числителя необходимо предварительно вычислить параметр d. Рис.3 показывает такой порядок вычислений. В этом случае общее время вычисления параметра t составит 2 операции умножения и 1 операция деления.

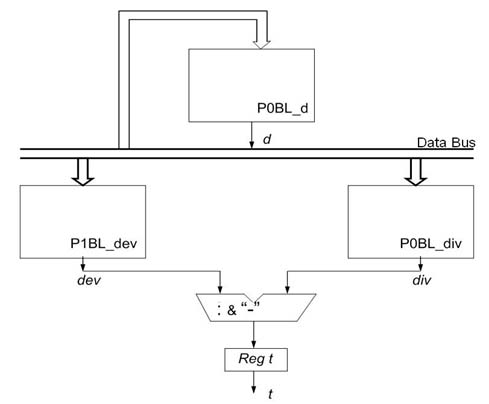
Рисунок 3 – Последовательно–параллельная реализации выражений (3)–(5)

Если для вычисления dev вместо блока с P1BL структурой применить блок с P0BL структурой, а затем к результату (dev0) прибавить параметр d (выражения 6), то выражения (3), (4) и первая часть из (6) могут быть рассчитаны параллельно (рис.4).

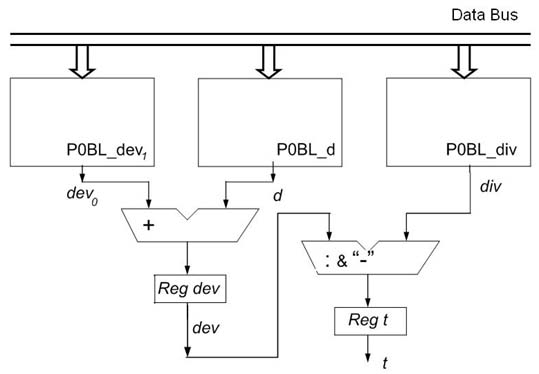
Рисунок 4 – Параллельная реализации выражений (3)–(5)

В этом случае общее время вычисления параметра t составит 1 операцию умножения, 1 операцию сложения и 1 операцию деления, что существенно быстрее предыдущей реализации.

Литература:

1. Метод трассировки лучей – [Электронный ресурс]. – Режим доступа: http://portal.tpu.ru:7777/SHARED/r/RUBINFC/academic/Tab1/лекция%202.pdf
2. NVIDIA Launches The World's First Interactive Ray Tracing Engine – [Электронный ресурс]. – Режим доступа: http://www.nvidia.com/object/io_1249366628071.html
3. Malcheva R., Yunis М. An Acceleration of FPGA–based Ray Tracer // European Scientific Journal, 2014. –Vol.10. – N7. – PP.186–190.