МАРШИРУЮЩИЕ КУБЫ:  АЛГОРИТМ ДЛЯ ПОСТРОЕНИЯ 3D ПОВЕРХНОСТИ ВЫСОКОГО РАЗРЕШЕНИЯ

Авторы:William E. Lorensen, Harvey E. Cline

Автор перевода: Сафонов М. Д.

Источник(англ.) :http://www.eecs.berkeley.edu/~jrs/meshpapers/LorensenCline.pdf

АННОТАЦИЯ

Мы представляем новый алгоритм под названием марширующие кубы, который создает треугольные модели поверхностей постоянной плотности из медицинских 3D снимков. Используя подход разделяй и властвуй для генерации связи между срезами, мы создаем таблицу, которая определяет топологию треугольника. Алгоритм обрабатывает медицинские 3D данные в порядке сканирования и вычисляет вершины треугольника используя линейную интерполяцию. Мы находим градиент исходных данных, нормализуем его, и используем его в качестве основы для затенения модели. Детали в изображениях, полученных из сгенерированной поверхности модели, являются результатами сохранения связей между срезами, данными поверхности и градиентом исходных 3D данных. Результаты компьютерной томографии (КТ), магнитно-резонансной томографии (МРТ) и однофотонной эмиссионной компьютерной томографии (ОФЭКТ) иллюстрируют качество и функциональность марширующих кубов. Также рассмотрены улучшения, сокращающие время обработки и предоставляющие возможность добавления твердотельного моделирования.

Ключевые слова: компьютерная графика, медицинские изображения, реконструкция поверхности.

1. ВВЕДЕНИЕ

Трехмерные анатомические поверхности представляют собой важный инструмент в медицине. Изображения этих поверхностей, построенные из массива 2D снимков, полученных от компьютерной томографии (КТ), магнитно-резонансной томографии (МРТ) и однофотонной эмиссионной компьютерной томографии (ОФЭКТ), помогают врачам распознать сложные анатомические процессы в снимках. Интерпретация медицинских 2D изображений требует специальной подготовки, и хотя радиологи имеют эти навыки, они должны часто сообщать о своих интерпретациях лечащими врачами, которые иногда испытывают трудности с визуализацией в 3D анатомии.

Исследования свидетельствуют о применении медицинских 3D изображений в различных областях. Визуализация сложных переломов вертлужной впадины [6], краниофациальных аномалий [17,18], и внутричерепных структур[13] свидетельствуют о потенциале трехмерного изучения костных структур. Применение в лучевой терапии [27,11] и хирургическом планировании [4,5,31] демонстрируют наглядность 3D методов в сочетании с 3D изображениями поверхностей. Применение в кардиологии включает в себя визуализацию артерии [2,16] и наглядное моделирование для расчета площади поверхности и её объема [21].

Существующим 3D алгоритмам не хватает деталей, а также они иногда демонстрируют артефакты. Мы представляем новый алгоритм построения 3D поверхности с высоким разрешением, который конструирует модели с беспрецедентной детализацией. Этот новый алгоритм, называемый марширующие кубы, создает полигональное представление поверхностей постоянной плотности из массива 3D данных. Полученная модель может быть отображена с помощью обычных алгоритмов графического рендеринга, реализованного в программном или аппаратном обеспечении.

После описания информационного потока для медицинских 3D приложений, мы опишем соответствующую работу и обсудим её недостатки. Далее мы опишем алгоритм на предмет усовершенствования по эффективности и функциональности, а затем проведем исследование с использованием трех различных методов для медицинских изображений для иллюстрации возможностей нового алгоритма.

2. ИНФОРМАЦИОННЫЙ ПОТОК ДЛЯ ТРЕХМЕРНЫХ МЕДИЦИНСКИХ АЛГОРИТМОВ

Медицинское применение 3D графики состоит из четырёх шагов (рисунок 1). Несмотря на то, что последние три шага можно объединить в один алгоритм, мы логически разбиваем процесс следующим образом:

1. Получение данных

Первый шаг выполняется средствами медицинского оборудования, в результате чего мы получаем массив 2D снимков пациента. Эти данные выборочно зависят от способа сбора данных.

Рентгеновская компьютерная томография (КТ) измеряет пространственно изменяющийся рентгеновский коэффициент ослабления [3], КТ-изображения показывают внутреннюю структуру. КТ часто используется, чтобы посмотреть на структуру кости, хотя возможна визуализация мягких тканей.

Магнитно-резонансная томография (МРТ) измеряет три физических свойства [20]. Одним из свойств является распределение подвижных ядер водорода и показывает общую структуру в пределах среза. Остальные два свойства измерения времени распада ядер. МРТ – это новый метод, показывающий превосходный контраст между различными мягкими тканями. Однако, разнообразие тканей представляет проблему для построения 3D поверхности и требует специальных методов для селективного извлечения поверхности и его отображения.

Техника третьего сбора, однофотонной эмиссионной компьютерной томографии (ОФЭКТ) измеряет излучение гамма-лучей [24]. Источником этих лучей является радиоактивный изотоп распределенный в организме. В дополнение к структуре, ОФЭКТ может показать наличие крови в структурах с гораздо более низкой дозой контраста, чем требуется при КТ.

2. Обработка изображения

Некоторые алгоритмы используют методы обработки изображений, чтобы найти необходимые структуры в 3D-данных [1,32,30,29] или фильтровать исходные данные. Данные МРТ, в частности, требуют обработки изображения, чтобы выбрать соответствующую структуру.

3. Построение поверхности

Построение поверхности является темой данной статьи, предполагает создание поверхностной модели из 3D данных. Модель, как правило, состоит из элементов 3D-объема (вокселей) или многоугольников. Пользователи выбирают нужную поверхность, указав значение плотности, этот шаг может также включать в себя создание разреза или ограниченных поверхностей.

4. Отображение

После создания поверхности,отображение поверхности с помощью методов рендеринга является последним шагом.

Рисунок 1 – Информационный поток для трехмерных медицинских алгоритмов

3. АНАЛОГИЧНЫЕ РАБОТЫ

Существуют несколько подходов к решению задачи построения 3D поверхности. Более ранний метод [23] начинается с определения контура поверхности и соединения контура друг за другом со срезами изображения треугольниками. К сожалению, если существует более одного контура поверхности на отрезке, возникают сложности при определении того, какие контуры необходимо соединить [14]. Непосредственное вмешательство пользователя может помочь решить некоторые из этих [8] неясностей. Тем не менее, в клинических условиях взаимодействие с пользователем должно быть сведено к минимуму.

Другой подход, разработанный Г. Германом и его коллегами [19] создает поверхности из cuberilles. Cuberille – это рассечение пространства на равные кубы (так называемые воксели) с помощью трех ортогональных наборов параллельных плоскостей [7]. Хотя существует много способов отображения модели cuberille, наиболее реалистичные изображения получаются когда используется градиент, вычисленный из cuberilles в окрестности, с поиском оттенка точки на модели [15]. Мигэр [25] использует представление октодерева для сжатия хранилища 3D данных, что позволяет быстро манипулировать и отображать воксели.

Фаррелл [12] использует метод бросания лучей чтобы найти 3D поверхность, но вместо тени изображения с серой шкалой, использует освещенность для отображения поверхности. В другом методе бросания лучей, Хон [22], после нахождения поверхности вдоль луча, вычисляет градиент вдоль поверхности и использует этот градиент, масштабируя соответствующими значениями для создания градаций серого для изображения.

Другой подход, используемый в клинике Майо [26], показывает объем плотности, а не поверхность. Этот метод дает, по сути, обычный теневой график, который можно рассматривать с произвольными углами. Движение усиливает эффект трехмерности, полученный с использованием объемной модели.

Каждый из этих методов построения поверхности и отображения несовершенен, поскольку они не учитывают полезную информацию в исходных данных. Алгоритмы соединения контуров не учитывают связность между срезами, которая существует в исходных данных. Cuberille подход, который для представления поверхности использует блоки в 3D-пространстве, пытается восстановить информацию о затенении блоков. Методы бросания лучей либо используют только глубину затенения, либо аппроксимируют затенение с ненормированным градиентом. Так как они показывают все значения, а не только те, которые видны с данной точки зрения, трехмерное ощущение достигается благодаря движению.

Наш подход использует информацию из исходных 3D данных, для получения возможности соединения между срезами, расположения поверхности и градиента поверхности. Полученная в результате модель треугольников может быть отображена на обычных графических систем отображения с использованием алгоритмов стандартного рендеринга.

4. АЛГОРИТМ МАРШИРУЮЩИЕ КУБЫ

В нашем подходе есть два основных шага к проблеме построения поверхности. Во-первых, мы находим поверхность, соответствующую заданным пользователем данным и создаем треугольники. Затем, чтобы обеспечить качественное изображение поверхности, мы вычисляем нормали к поверхности в каждой вершине каждого треугольника.

Алгоритм марширующие кубы использует подход разделяй и властвуй, чтобы найти поверхность в логическом кубе, созданного из восьми пикселей; для каждой из двух смежных сторон (рисунок 2).

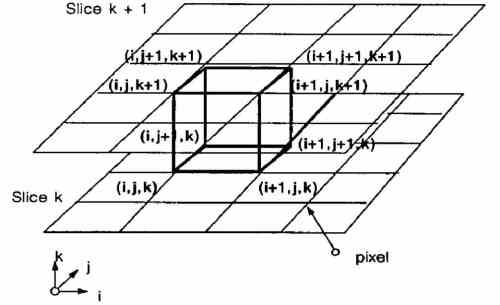
Рисунок 2 – Марширующие кубы

Алгоритм определяет, как поверхность пересекает этот куб, затем перемещается (или марширует) к следующему кубу. Чтобы найти поверхностное пересечение в кубе, мы присваиваем 1 к вершине куба, если значение данных в этой вершине превышает (или равно) значению поверхности, которую мы строим. Эти вершины находятся внутри (или на) поверхности. Вершины куба со значениями ниже поверхности получают нулевое значение и находятся вне поверхности. Поверхность пересекает ребра куба, где одна вершина находится вне поверхности (один), а другая находится внутри поверхности (ноль). При таком допущении мы определяем топологию поверхности внутри куба, нахождение пересечения определяется позже.

Поскольку существует восемь вершин в каждом кубе и два возможных значения, внутри и снаружи, есть только 2⁸= 256 способов с которыми поверхность может пересекаться с кубом. Перечисляя эти 256 случаев, мы создаем таблицу, чтобы рассмотреть области пересечения поверхности, учитывая номера вершин куба. Таблица содержит области пересечения для каждого конкретного случая.

Триангулировать 256 случаев возможно, однако это утомительно и подвержено ошибкам. Две различные симметрии куба уменьшают проблему с 256 до 14 случаев. Во-первых, топология триангулированной поверхности не изменяется, если отношения значений поверхности к кубам станет обратным. Дополнительные случаи, когда значения в вершинах больше, чем значение поверхности, переставлены с теми, в которых значения меньше, чем значение поверхности, так как они эквивалентны. Таким образом, только те случаи, в которых значения от нуля до четырех вершин больше, чем значение поверхности, должны быть рассмотрены,в таком случае число возможных случаев сокращается до 128. Используя второе свойство симметрии, осевую симметрию, мы свели задачу к 14 возможным случаям. На рисунке 3 показана триангуляции для 14 моделей.

Рисунок 3 – Триангулированные кубы

Случай под номером 0 является самым простым и имеет место, когда все значения вершин выше (или ниже) выбранного значения, и не производит треугольников. Следующий образец под номером 1 имеет место, когда поверхность отделяет от вершины остальные семь вершин, в результате чего получается один треугольник, образуемый тремя краевыми пересечениями. Другие случаи производят несколько треугольников. Перестановка этих 14 основных моделей с использованием комплиментарной и осевой симметрии производит 256 случаев.

Мы создали индекс для каждого конкретного случая, исходя из состояния вершины. С использованием нумерации вершин на рисунке 4, получаем восьмибитный индекс, содержащий один бит для каждой вершины.

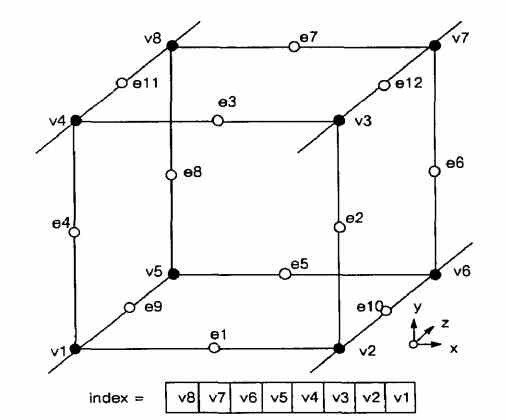
Рисунок 4 – Нумерация куба

Этот показатель служит указателем в таблице, которая дает все области пересечения для данной конфигурации куба.

Используя данный индекс, можно сказать какой край пересекает поверхность, мы можем интерполировать поверхность пересечения вдоль края. Мы используем линейную интерполяцию, но экспериментировали с интерполяция более высоких степеней. Так как алгоритм производит по меньшей мере один или максимум четыре треугольника на каждый куб, то интерполяции более высоких степеней показывают небольшое улучшение по сравнению с линейной интерполяцией.

Последним шагом в алгоритме марширующих кубов является вычисление единичной нормали для каждой вершины треугольника. Поверхность постоянной плотности имеет нулевой градиент вдоль поверхности в тангенциальном направлении; следовательно, направление вектора градиента g нормально расположено к поверхности. Мы можем использовать этот факт для определения вектора n нормали плоскости, если величина градиента, |g| отлична от нуля. К счастью, на поверхности между двумя типами тканей различной плотности, градиент вектора равен нулю. Вектор градиента, g, является производной от функции плотности.

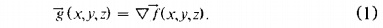
Для оценки вектора градиента на поверхности, мы сначала оценим вектор градиента в вершине куба и линейно интерполируем градиент в точке пересечения. Градиент в вершине куба (i,j,k), оценивается с помощью центральных разностей вдоль трех осей координат:

,

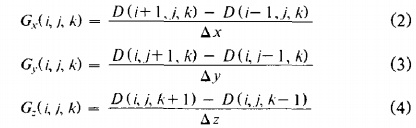где D (i,j,k) есть плотность на пиксель (i, j) в срезе k, а Ax, Ay, Az являются длинами ребер куба. Разделив градиент на длину получим единичную нормаль в вершине, требуемой для отрисовки. Мы линейно интерполируем эту нормаль к точке пересечения. Обратите внимание, что для вычисления градиента на всех вершинах куба, мы держим четыре среза в памяти сразу.

Таким образом, марширующие кубы строят поверхность из трехмерного набора данных следующим образом:

1. Считывание четырех срезов в память.

2. Сканирование двух среза и создание куба из четырех соседних на одном срезе и из четырех соседей на следующем срезе.

3. Вычисление индекса для куба путем сравнения значений плотности восьми вершин куба со значениями поверхности.

4. Используя индекс, просмотр списка ребер из таблицы.

5. Поиск области пересечения поверхности с помощью линейной интерполяции с использованием плотности в каждой вершине.

6. Вычисление единичной нормали в каждой вершине куба с использованием центральных разностей. Интерполирование нормали к каждой вершине треугольника.

7. Вывод вершин треугольника и нормалей вершин.

5. УЛУЧШЕНИЯ БАЗОВОГО АЛГОРИТМА

Мы сделали несколько улучшений к первоначальному алгоритму марширующих кубов, которые делают алгоритм более быстрым и добавляют возможность твердотельного моделирования.

5.1 Улучшение эффективности

Усовершенствования эффективности позволяют алгоритму воспользоваться согласованностью между пикселями, линиями и срезами. Для кубов в пределах исходных данных ( те, которые не относятся к срезу 0, линии 0 или пикселю 0), необходимо интерполировать только три новые ребра. Мы можем получить другие девять ребер из предыдущих срезов, линий или точек. На рисунке 5, заштрихованные кружки представляют значения, доступные из предыдущих расчетов; только края 6, 7, и 12 должны быть рассчитаны для нового куба.

Особые случаи присутствуют вдоль границ данных, но, рассматривая эти случаи, мы можем ограничится одним расчетом вершины. На практике мы только сохраним предыдущие пиксели и линии пересечения, так как объем памяти, необходимый для сохранения пересечения предыдущего среза является большим. Использование согласованности ускоряет алгоритм в три раза.

Уменьшение разрешения среза, путем усреднения четырех пикселей в одно целое, уменьшает число треугольников, повышает эффективность построения поверхности и сглаживает изображение. Несмотря на то, что есть некоторая потеря детализации в усредненных срезах, усреднение делает число треугольников более управляемым для срезов с высоким разрешением.

Рисунок 5 – Согласованность

5.2 Функциональные улучшения

Для алгоритма мы добавили возможность твердотельного моделирования. Булевы операции позволяют разрезание и перемещение твердых моделей, а также извлечение нескольких поверхностей. В медицинской практике, разрезание аналогично выполнению хирургической операции, а перемещение (и текстурирование) аналогично медицинской технике переформатирования. Мы используем индекс куба, описанный ранее, для логических операций на поверхностях. Рассмотрим три значения индекса:

Индекс = 0 для кубов вне поверхности.

Индекс = 255 для кубов внутри поверхности.

0 < индекс < 255 для кубов на поверхности.

Твердотельное моделирование использует понятия внутри, снаружи и на для создания поверхности. Аналитические функции также обеспечивают ту же информацию; так, например, уравнение плоскости, ax + by + cz - d говорит о том, где данная точка лежит по отношению к плоскости. Пусть ∼S, δS, и S представляют собой множества точек, которые находятся снаружи, на и внутри поверхности, соответственно. Соответственно рисунку 6 мы строим таблицу истинности, как показано на рисунке 7, для булевой операции пересечения.

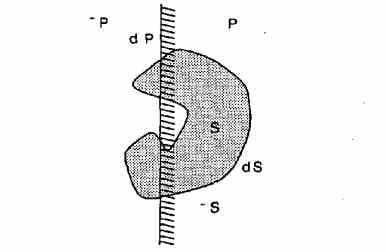
Рисунок 6 – Отношение точка/поверхность

Девять записей в таблице истинности описывают, что делать, когда две поверхности имеют заданный индекс. Крестики означают отсутствие операции, вход для (S,∼P) показывает, что куб, о котором идет речь, внутри одной поверхности, и снаружи другой, что приводит к отсутствию треугольников. Запись (δS, P) производит треугольники с поверхностью S, в то время как запись (S, δP) производит треугольники с поверхности P. (δS, δP) запись создается, когда куб на обеих поверхностях, требует специальной обработки.

Рисунок 7 – Таблица истинности

6. РЕАЛИЗАЦИЯ

Марширующие кубы, написанные на С, запускались на Sun Workstations под Unix, на VAX под VMS и на IBM 3081 под IX/370. Мы демонстрируем модели используя программу General Electric Graphicon 700. Graphicon отображает наши модели со скоростью 10000 треугольников в секунду. Время выполнения зависит от количества поверхностей и плотности исходных данных. Время создания модели на VAX 11/780 варьируется от 100 секунд до 30 минут. Время для одних и тех же исследований на IBM 3081 в двенадцать раз быстрее. Число треугольников в модели поверхности пропорциональна площади поверхности. Это число может быть большим (более 500 000 в некоторых случаях), поэтому мы уменьшаем его с помощью срезанных плоскостей. Кроме того, иногда мы уменьшаем разрешение исходных данных путем фильтрации, производя несколько более гладкую поверхность с некоторой потерей разрешения.

7. РЕЗУЛЬТАТЫ

Мы применили марширующие кубы на данных полученных от КТ, МРТ и ОФЭКТ, а также на данных, полученных от аналитических функций. Мы представили три тематические исследования, иллюстрирующие качество построенных поверхностей и некоторых вариантов моделирования. Каждое изображение было разрешением 512 на 512 без сглаживания.

7.1 Компьютерная томография

Первый случай представляет собой исследование КТ головы двенадцатилетнего мальчика с отверстием в черепе возле левой стороны носа, 93 аксиальных среза толщиной 1,5 мм, с размерами пикселей в 0,8 мм. На рисунках 8 и 9 представлены костная поверхность и поверхность мягких тканей соответственно. Трубка во рту пациента присутствует для ввода анестезии во время процесса сканирования. Изображение поверхности мягких тканей показывает мелкие детали, которые включают в себя проколотое ухо пациента и клейкую ленту на лице. Хотя эти детали не являются клинически значимыми, они показывают разрешение, присутствующее в построенной поверхности. На рисунке 10 представлен вид наклонной поверхности мягких тканей, который показывает носовые и ушные проходы. На рисунке 11 представлен сагиттальный разрез, текстуры исходных данных КТ, показан срез данных по отношению к построенной поверхности. Поверхность костных тканей содержит 550 000 треугольников, в то время как поверхность мягких тканей имеет 375 000.

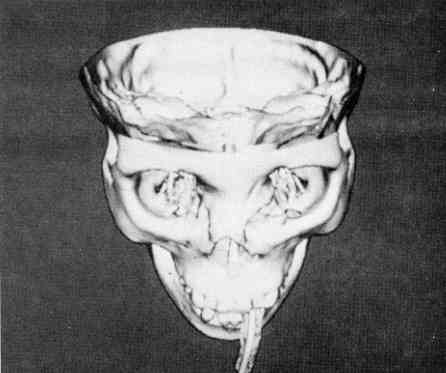
Рисунок 8 – Костная поверхность

Рисунок 9 – Поверхность мягких тканей

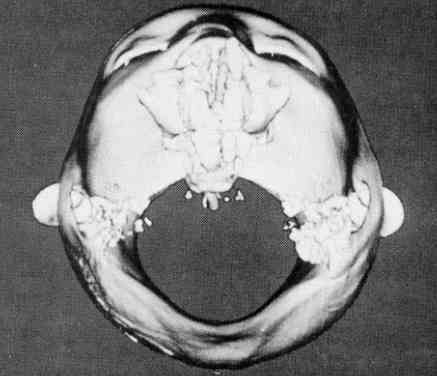
Рисунок 10 – Поверхность мягких тканей, вид сверху

Рисунок 11 – Сагиттальный разрез

7.2 Магнитно-резонансная томография

МРТ взрослого мужчины состоит из 128ми 1,9 мм корональных срезов. Из-за сложной анатомии, присутствующей в срезах МРТ, мы показываем на рисунке 12 текстуру поверхности пересечения с поверхностью кожи. Мы показываем сагиттальной разрез, чтобы проиллюстрировать способность алгоритма для интерполяции текстуры на плоскости разреза. Самая большая модель поверхности в последовательности содержит 330 000 треугольников, в том числе треугольников на поверхности разреза.

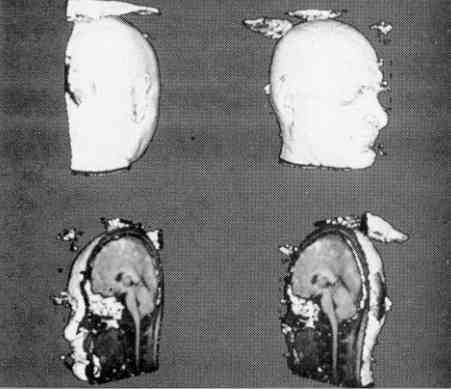
Рисунок 12 – Повернутая последовательность срезов МРТ головы

7.3 Однофотонная эмиссионная компьютерная томография

Исследование ОФЭКТ, состоящее из 29 корональных срезов сердца, показывает производительность алгоритма на данных с низким разрешением. Были использованы пиксельные данные разрешением 64 на 64. На рисунке 13 показана поверхность бассейна крови в диастоле, состоящее из 5000 треугольников. Большой сосуд в нижней части изображения – это нисходящая аорта.

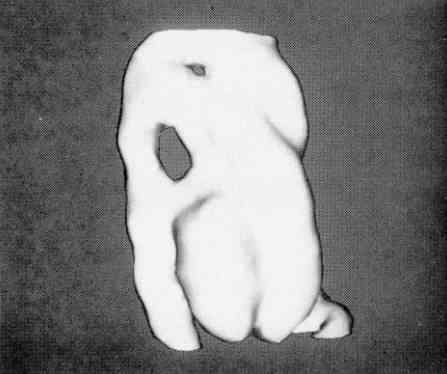
Рисунок 12 – Поверхность бассейна крови в диастоле

8. ЗАКЛЮЧЕНИЕ

Марширующие кубы – это новый алгоритм для построения 3D поверхности, который дополняет снимки КТ, МРТ, а также данные ОФЭКТ, давая врачам трехмерные анатомические изображения. Алгоритм использует таблицу областей пересечений, чтобы описать, как поверхность прорезает каждый куб в 3D наборе данных. Дополнительный реализм достигается путем расчета, из исходных данных, нормированного градиента. Полученная многоугольная структура может отображаться на обычных системах отображения графики. Когда аппаратные средства CAD увеличат скорости и емкости, мы ожидаем, что марширующие кубы будут получать более широкое применение в практических, клинических условиях.

Недавно мы разработали другой алгоритм построения поверхности высокого разрешения под названием деление кубов, который генерирует точки, а не треугольники [10]. По мере увеличения разрешения увеличивается объем медицинских данных, а количество треугольников приближается к числу пикселей в отображаемом изображении. Плотность точек поверхности выбирается для покрытия дисплея растра. Оба алгоритма производят изображения одного и того же качества.

9. Благодарности

Мы благодарим C. Crawford из General Electric's Medical Systems за стимулирование нашей работы в этой области. На протяжении всего проекта, он предоставлял нам данные и поддержку для улучшения алгоритма. R. Redington из нашей лаборатории Medical Diagnostics Branch за предоставленные стабильные условия исследовательской среды и понимание практического применения 3D в медицине. W. Leue оказал нам помощь в преобразовании между различными форматами медицинских данных и предоставляемых интерфейсов для нашего МРТ оборудования.

10. ССЫЛКИ

[1] Artzy, E., Frieder, G., and Herman, G.T. The Theory, Design, Implementation and Evaluation of a Three-Dimensional Surface Detection Algorithm. Computer Graphics and Image Processing, 15, 1 (January 1981), 1-24.

[2] Barillot, C., Gibaud, B., Scarabin, J., and Coatrieux, J. 3D Reconstruction of Cerebral Blood Vessels. IEEE Computer Graphics and Applications 5, 12 (December 1985), 13-19.

[3] Bates, R. H., Garden, K. L., and Peters, T. M. Overview of Computerized Tomography with Emphasis on Future Developments. Proc. of the IEEE 71, 3 (March 1983), 356-372.

[4] Bloch, P. and Udupa, J. K. Application of Computerized Tomography to Radiation Therapy and Surgical Planning. Proc. of the IEEE 71, 3 (March 1983), 351-355.

[5] Brewster, L. J., Trivedi, S. S., Tut, H. K., and Udupa, J. K. Interactive Surgical Planning. IEEE Computer Graphics and Applications 4, 3 (March 1984), 31-40.

[6] Burk, D. L., Mears, D. C., Kennedy, W. H., Cooperstein, L. A., and Herbert, D. L. Three-Dimensional Computed Tomography of Acetabula Fractures. Radiology 155, 1 (1985), 183-186.

[7] Chen, L., Herman, G. T., Reynolds, R. A., and Udupa, J. K. Surface Shading in the Cuberille Environment. IEEE Computer Graphics and Applications 5, 12 (December 1985), 33-43.

[8] Christiansen, H. N. and Sederberg, T. W. Conversion of Complex Contour Line Definitions into Polygonal Element Meshes. Computer Graphics 12, 3 (August 1978), 187-192.

[9] Cline, H. E., Dumoulin, C. L., Lorensen, W. E., Hart, H. R., and Ludke, S. 3D Reconstruction of the Brain from Magnetic Resonance Images. Magnetic Resonance Imaging (1987, to appear).

[10] Cline, H. E., Lorensen, W. E., Ludke, S, Crawford, C. R., and Teeter, B. C. High-Resolution ThreeDimensional Reconstruction of Tomograms. Medical Physics (1987, to appear).

[11] Cook, L. T., Dwyer, S. J., Batnitzky, S., and Lee, K. R. A Three-Dimensional Display System for Diagnostic Imaging Applications. IEEE Computer Graphics and Applications 3, 5 (August 1983), 13-19.

[12] Farrell, E. J. Color Display and Interactive Interpretation of Three-Dimensional Data. IBM J. Res. Develop 27, 4 (July 1983), 356-366.

[13] Farrell, E. J., Zappulla, R., and Yang, W. C. Color 3D Imaging of Normal and Pathologic Intracranial Structures. IEEE Computer Graphics and Applications 4, 9 (September 1984), 5-17.

[14] Fuchs, H., Kedem, Z. M., and Uselton, S. P. Optimal Surface Reconstruction from Planar Contours. Comm. of the ACM 20, 10 (October 1977), 693-702.

[151 Gordon, D. and Reynolds, R. A. Image Space Shading of 3-Dimensional Objects. Computer Graphics and Image Processing 29, 3 (March 1985), 361-376.

[16] Hale, J. D., Valk, P. E., and Watts, J. C. MR Imaging of Blood Vessels Using Three-Dimensional Reconstruction: Methodology. Radiolo,xv 157, 3 (December 1985), 727-733.

[17] Hemmy, D. C., David, D. J., and Herman, G. T. Three-Dimensional Reconstruction of Craniofacial Deformity Using Computed Tomography. Neurosurgery 13, 5 (November 1983), 534-541.

[18] Hemmy, D. C. and Tessier, P. L. CT of Dry Skulls with Craniofacial Deformities: Accuracy of ThreeDimensional Reconstruction. Radiology 157, 1 (October 1985), 113-116.

[19] Herman, G. T. and Udupa, J. K. Display of 3D Digital Images: Computational Foundations and Medical Applications. IEEE Computer Graphics and Applications 3, 5 (August 1983), 39-46.

[20] Hinshaw, W. S. and Lent, A. H. An Introduction to NMR Imaging: From the Bloch Equation to the Imaging Equation. Proc. of the IEEE 71, 3 (March 1983), 338-350.

[21] Hoffman, E. A. and Ritman, E. L. Shape and Dimensions of Cardiac Chambers: Importance of CT Section Thickness and Orientation. Radiology 155, 3 (June 1985), 739-744.

[22] Hohne, K. H. and Bernstein, R. Shading 3D-Images from CT Using Gray-Level Gradients. IEEE Trans. on Medical Imaging MI-5, 1 (March 1986), 45-47.

[23] Keppel, E. Approximating Complex Surfaces by Triangulation of Contour Lines. IBM J. Res. Develop 19, 1 (January 1975), 2-11.

[24] Knoll, G. F. Single-Photon Emission Computed Tomography. Proc. of the IEEE 71, 3 (March 1983), 320-329.

[25] Meagher, D. J. Geometric Modeling Using Octree Encoding. ComputerGraphics and Image Processing 19, 2 (June 1982), 129-147.

[26] Robb, R. A., Hoffman, E. A., Sinak, L. J., Harris, L.D.,and Ritman, E. L. High-Speed Three-Dimensional X-Ray Computed Tomography:The Dynamic Spatial Reconstructor.Proc. of the IEEE 71, 3 (March 1983),308-319.

[27] Sunguroff, A. and Greenberg, D. Computer Generated Images for Medical Application. Computer Graphics 12, 3 (August 1978), 196-202.

[28] Sutherland, I. E. and Hodgman, G. W. Reentrant Polygon Clipping. Comm. of the ACM 17, 1 (January 1974), 32-42.

[29] Trivedi, S, S., Herman, G. T., and Udupa, J. K. Segmentation Into Three Classes Using Gradients. IEEE Trans. on Medical Imaging MI-5, 2 (June 1986), 116-119.

[30] Udupa, J. K. Interactive Segmentation and Boundary Surface Formation for 3-D Digital Images. Computer Graphics and Image Processing 18, 3 (March 1982), 213-235.

[31] Vannier, M. W., Marsh, J. L., and Warren, J. O. Three Dimensional CT Reconstruction Images for Craniofacial Surgical Planning and Evaluation. Radiology 150, 1 (January 1984), 179-184.

[32] Zucker, S. W. and Hummel, R. A. A ThreeDimensional Edge Operator. IEEE Trans. on Pattern Analysis and Machine Intelligence PAMI-3, 3 (May 1981), 324-331.