Задачи построения триангуляции Делоне и триангу- ляции Делоне с ограничениями являются одними из базо- вых в вычислительной геометрии и машинной графике [1]. Триангуляция широко применяется в геоинформатике для моделирования поверхностей и анализа геометриче- ской близости, в машинной графике – для построения моделей трехмерных объектов, в различных методах конечных элементов.

Впредыдущих работах автором проводились иссле- дования различных алгоритмов построения триангуляции Делоне и триангуляции с ограничениями. В [2] обосновы- вается выбор итеративного алгоритма построения триан- гуляции Делоне с динамическим кэшированием как наи- более эффективного и простого в реализации среди всех известных автору алгоритмов. Этот алгоритм имеет в среднем линейную относительно количества исходных точек трудоемкость. В [3] приводится алгоритм построе- ния триангуляции Делоне с ограничениями, построенный на основе простого итеративного алгоритма.

Вприводимых ранее автором описаниях алгоритмов предполагалось, что координаты исходных для построения триангуляции точек и структурных линий представлены в виде вещественных чисел, и так же определена сама струк- тура триангуляции. Никаких специальных оценок потенци- альных потерь точности при вычислениях не проводилось [2–3]. Это же неявное допущение о бесконечной точности вещественных вычислений свойственно и всем другим работам, известнымавтору поданнойтематике.

Вданной работе в явном виде оцениваются возмож- ные потери точности вычислений, предлагается явный переход от арифметики с плавающей точкой к арифмети- ке с фиксированной точкой (в частности, к целочислен- ным вычислениям). Также рассматривается задача по- строения триангуляции Делоне с ограничениями в усло- виях вставки пересекающихся структурных линий и пока- зывается, что прямая реализация может привести к значи- тельным затратам по времени и даже к зацикливанию алгоритма. Для устранения таких эффектов предлагается явно контролировать точность вычислений, избегая по- строения слишком близких точек и проведения структур- ных ребер вблизи узлов триангуляции.

Анализ алгоритмов

В настоящее время наиболее распространенной структурой для представления триангуляции без ограничений является структура, в которой в явном виде представлены точки и треугольники [2, 4, 5]:

Точка = record

X, Y: Координата; end;

Треугольник = record

P: array [1..3] of Указатель_на_точку;

T: array [1..3] of Указатель_на_треугольник; end;

Обычно координаты представляются в виде ве- щественных чисел.

Рассмотрим основные шаги работы итеративно- го алгоритма построения триангуляции Делоне [2].

Пусть имеется N исходных входных двумерных вещественных точек (xi, yi). Вначале на базе некото- рых трех неколлинеарных исходных точек строится первый треугольник, который и образует текущую триангуляцию. Затем все оставшиеся точки пооче- редно добавляются в триангуляцию. Вставка оче- редной точки разбивается на два этапа.

1.Локализация точки в триангуляции. Выполня- ется поиск ранее построенного треугольника, в ко- торый попадает очередная точка, либо, если точка не попадает в триангуляцию, то определяется бли- жайший к точке треугольник.

2.Вставка точки. Если точка попала строго на ранее вставленную точку, то эта точка отбрасывает- ся. Если точка попала на ребро триангуляции, то треугольники по разную сторону от ребра разбива- ются на два новых треугольника. Если точка попала внутрь некоторого треугольника, то он разбивается на 3 новых треугольника. Если точка не попала в триангуляцию, то строится 1 или более новых тре- угольников. После этого производятся локальные проверки выполнения условия Делоне для всех вновь построенных треугольников.

Взадаче построения триангуляции Делоне с ог- раничениями помимо исходных точек дополни- тельно задается множество ломаных (структурных линий), при этом требуется, чтобы все эти ломаные проходили строго по ребрам триангуляции, не пере- секая треугольники.

Эта задача обычно решается в два этапа. Внача- ле строится обычная триангуляция Делоне без огра- ничений на основе всех исходных точек и узловых точек структурных линий. Затем выполняется по- следовательная вставка отрезков ломаных струк- турных линий. При этом возможна ситуация, когда очередное вставляемое структурное ребро будет конфликтовать с уже ранее вставленным. В таком случае либо новое ребро отбрасывается, либо уже вставленное ребро ивновьвставляемое разбиваются на две части точкой их пересечения.

Для поддержки понятия структурных линий в структуру триангуляции вводятся дополнительные изменения обычно следующего вида:

Точка = record

X, Y: Координата; end;

Треугольник = record

P: array [1..3] of Указатель_на_точку;

T: array [1..3] of Указатель_на_треугольник; R: array [1..3] of Указатель_на_ребро;

end;

Ребро = record

P: array [1..2] of Указатель_на_точку;

T: array [1..2] of Указатель_на_треугольник; end;

При этом ребро в явном виде хранится только для структурных ребер. Если ребра треугольника не являются структурными, то соответствующие ссыл- ки R[1]=R[2]=R[3]=0 являются пустыми.

Однако за такой внешней простотой описания алгоритмов скрываются многочисленные детали ре- ализации. Перечислим основные подзадачи.

Задача 1. Проверка совпадения двух заданных точек. Эта проблема является особенно актуальной в случае использования вещественной арифметики с плавающей точкой. Как известно, сравнение пла- вающих вещественных чисел на равенство произво- дится всегда с заданной точностью ε. Здесь опреде- ляющим является выбор значения ε.

Несмотря на кажущуюся простоту, данная про- блема имеет далеко идущие последствия. В силу своей ограниченной точности обычные веществен- ные вычисления на компьютерах не обладают мно- гими свойствами истинно вещественных чисел. На- пример, если мы используем числа, хранящиеся в памяти компьютера с помощью 3 значимых цифр, то результат вычисления следующих выражений может не совпадать, т.е. нарушается свойство ассо- циативности:

(100 +0,5) +0,5 ≅100 ≠ 101 ≅100 +(0,5 +0,5) .

Задача 2. Проверка взаимного расположения

двух точек относительно прямой, проходящей через две заданные точки. Данная задача обычно очень просто решается методами аналитической геометрии. Записываем уравнение прямой, прохо- дящей через две заданные точки – (x1,y1) и (x2,y2):

(x1 − x)(y2 − y) −(x2 − x)(y1 − y) = 0 .

Затем подставляем в это уравнение вместо x и y координаты тестовых точек (x3,y3) и (x4,y4). Если зна- чения выражений будут иметь одинаковый знак, то точки находятся по одну сторону от прямой, иначе – по разную. Результат выражения, равный нулю, бу- детозначатьпопаданиеточкистрогонапрямую.

Проблема заключается в потере точности проме- жуточных вычислений. Перемножая два n-значных числа, вообще говоря, получаем 2n-значное число. На практике это обычно не учитывается, и младшие n разрядов попросту отбрасываются. В итоге ре- зультат вычислений может показать, что тестовая точка лежит на прямой, хотя это не так. Для избав- ления от этого эффекта сравнение с нулем проводят с некоторой точностью ε. Несмотря на это, реальная точность вычислений все равно уменьшается в 2 ра- за, составляя не более n/2 исходных значащих цифр.

Задача 3. Проверка коллинеарности трех за-

данных точек. Эта задача является частным слу- чаем предыдущей, и ей свойственны те же пробле- мы с переполнением промежуточных вычислений.

Задача 4. Проверка взаимного расположения точкиитреугольника. Здесьтребуетсяопределить:

1)не совпадает ли точка с одной из вершин тре- угольника;

2)не попадает ли точка на одно из его ребер;

3) не попадает ли точка строго внутрь треугольни- ка. Новым является проверка попадания точки строго внутрьтреугольника. Эторешаетсяпутемтрехкратной проверки взаимного расположения заданной точки относительно различных ребер треугольника, т.е. так- жесводитсякпредыдущимзадачам.

Задача 5. Проверка порядка обхода трех задан-

ных точек. Здесь требуется определить, обходятся ли точки в заданном порядке по часовой стрелке или против. Эту задачу решаем, записывая уравнение прямой, проходящей через две заданные точки, и подставляя в уравнение координаты третьей точки. Послечегоанализируемзнаквыражения. Если

(x1 − x3 )(y2 − y3 ) −(x2 − x3 )(y1 − y3 ) < 0,

то точки обходятся по часовой стрелке, а если > 0 , то против (это верно для левосторонней системы координат, для правосторонней системы все будет наоборот).

В данном алгоритме возникает та же самая про- блема переполнения, что и при решении предыду- щих задач.

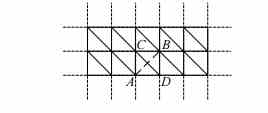
Задача6. ПроверкавыполненияусловияДелоне для двух заданных смежных треугольников. Дан-

ная задача может быть решена через классическое определение условия Делоне: внутрь окружности, описанной вокруг любого треугольника, не должны попадатьникакиеточкитриангуляции(рис. 1).

B

A

C

D

Рис. 1. Проверка условия Делоне

В этом случае записывается уравнение окружно- сти, проходящей через вершины одного из тре- угольников, и затем подставляется в уравнение про- тиволежащая точка второго треугольника:

x2 + y2		x	y	1
x2	+ y2	x	y	1	=0 .
1	1	1	1
x22 + y22		x2	y2 1
x32 + y32		x3	y3	1

На основе этого уравнения можно получить сле- дующий способ определения попадания заданной точки (x0,y0) внутрь окружности, описанной вокруг точек (x1,y1), (x2,y2) и (x3,y3). Положим:

y2−3 = y2 − y3 , y3−1 = y3 − y1 , y1−2 = y1 − y2 ,

a = x1 y2−3 + x2 y3−1 + x3 y1−2 ,
k = x2	+ y2	, m = x2	+ y2	, n = x2	+ y2	,
1	1	2	2	3	3

b= ky2−3 +my3−1 +ny1−2 ,

c= k(x2 − x3 ) +m(x3 − x1 ) +n(x1 − x2 ),

d=k(x2 y3 −x3 y2 ) +m(x3 y1 −x1 y3 ) +n(x1 y2 −x2 y1 ),

r = a(x02 + y02 ) −bx0 +cy0 −d.

Если r ≤ 0 , тоусловиеДелоневыполняется, иначе

– нет. Если исходные координаты точек имели n точ- ных знаков, то для выполнения вычислений указан- ным способом нам требуется использовать 4n-знач- ную арифметику, в частности, требуется уметь пере- множать2n-значныечисладляполучения4n-значных.

Другой способ проверки условия Делоне на ос- нове анализа углов треугольников приведен в [6]:

x2−0 = x2 − x0 , y2−0 = y2 − y0 , x3−0 = x3 − x0 , y3−0 = y3 − y0 , x3−1 = x3 − x1 , y3−1 = y3 − y1 , x2−1 = x2 − x1 , y2−1 = y2 − y1 ,

s= (x2−0 + x3−0 )(y2−0 + y3−0 ),

t= (x3−1 + x2−1 )(y3−1 + y2−1 ).

Если s < 0 и t < 0 , то условие Делоне не вы- полняется, иначе если s ≥ 0 и t ≥ 0 , то условие Де- лоне выполняется, иначе требуются еще дополни- тельные проверки:

u= (x2−0 − x3−0 )(y2−0 − y3−0 ),

v= (x3−1 − x2−1 )(y3−1 − y2−1 ), r = au +bv .

Если r ≥ 0 , то условие Делоне выполняется, иначе – нет.

Второй способ требует значительно меньшего количества элементарных операций, однако также требует использования 4n-значной арифметики для вычисления значения r.

В обоих способах если не используется специ- альная арифметика, то реальная точность вычисле- ний уменьшается в 4 раза, составляя не более n / 4 исходных значащих цифр.

Задача 7. Локализация точки в триангуляции.

Локализация точки в триангуляции состоит из вы- бора некоторого начального треугольника в триан- гуляции и последовательного перехода по тре- угольникам к цели. Автору известны два варианта решения данной задачи. Пусть (x0,y0) – заданная точка, T – начальный треугольник для поиска.

Вариант 1. Пусть (x,y) – центроид текущего тре- угольника T (среднее арифметическое координат вершин). Тогда в качестве следующего треугольни- ка T для перехода к цели будем брать тот из трех возможных соседей текущего треугольника, центр которого находится ближе к точке (x0,y0), чем теку- щее значение (x,y).

В этом варианте реальна ситуация, когда опреде- ляемый центр треугольника из-за потери точности вычислений оказывается вне самого треугольника, и тогда последующие вычисления теряют смысл и воз- можно зацикливание. Это вероятно при наличии длинных и узких треугольников, часто образующихся на границе триангуляции, а также вдоль структурных линий. Приведемпример. Пустьточностьвычислений составляет 3 знака, тогда центром треугольника T с координатами вершин (110;101), (111;101) будет точ-

ка (107;101) , лежащаявнесамоготреугольника. Более

того, эта точка может лежать даже не внутрисоседне- гокT треугольника, агораздодальше.

Вариант 2. Вычисляется начальная точка (x1, y1) как центроид начального треугольника T. Затем по-

следовательно производятся переходы к цели стро- го вдоль прямой (x1 , y1 ) −(x0 , y0 ) .

Вэтом варианте возможна та же самая проблема

свычислением центроида на первом шаге, что и в предыдущем, и алгоритм может зациклиться. Также здесь требуется отдельно учесть возможность попа-

дания на отрезок (x1 , y1 ) −(x0 , y0 ) каких-либо су-

ществующих узлов триангуляции.

Задача 8. Поиск точки пересечения двух пря-

мых. Данная задача возникает при построении триан- гуляции Делоне с ограничениями, когда обнаружива- ется, чтоочереднойвставляемыйотрезокпересекается с ранее вставленным структурным ребром триангуля- ции. Обычно при этом производится вставка новой точки в триангуляцию и разбиение существующего ребра этой точкой на две части. Только после этого вставляетсяновоеребро, такжеразбитоенадвечасти.

В данном алгоритме первой проблемой является то, что определяемая точка пересечения в силу ог- раниченности точности вычислений в большинстве случаев не лежит на ранее существовавшем ребре и не лежит на новом. Возможно, что эта точка лежит даже не в смежных с ребром треугольниках, поэто- му в результате разбиения старого ребра на части образуются новые «вывернутые» треугольники, раз- рушая структуру триангуляции. На рис. 2 приведен пример вставки ребра AB в триангуляцию, приво- дящей к пересечению с существующим ребром в точке S (пунктирными линиями размечена дискрет- ная координатная сетка). В результате округления точка пересечения окажется немного выше реаль- ной – в узле дискретной координатной сетки.

S

B

A

Рис. 2. Пример возможного «выворачивания» треугольников

Несмотря на кажущуюся экзотичность приведен- ного сценария возникновения ошибки, вероятность его велика уже при попытке вставить в триангуляцию нескольких десятков взаимно пересекающихся струк- турных ребер. Вдоль структурных ребер образуются многочисленные узкие вытянутые треугольники, ко- торыеисоздаютуказаннуюкритическуюситуацию.

Вторая проблема в задаче поиска точек пересе- чения связана непосредственно с самим используе- мым способом вычислений. Обычно точка пересе- чения (x, y) находится следующим образом:

a= (x1 − x3 )( y4 − y3 ) −( y1 − y3 )(x4 − x3 ),

b= (x4 − x3 )(y2 − y1 ) −( y4 − y3 )(x2 − x1 ),

x = x1 +a(x2 − x1 ) / b, y = y1 +a(y2 − y1 ) / b.

Здесь сложности возникают при нахождении точки пересечения двух «почти» коллинеарных от- резков. В результате потери точности возможно

значительное смещение найденных координат от реального значения. Кроме того, из-за потерь точ- ности мы можем предполагать, что отрезки пересе- каются, хотя это не так. Тогда попытка вычисления их пересечения может привести к значительному удалению найденной точки от самих отрезков (для «почти» коллинеарных отрезков).

Предлагаемые модификации

Большинство поставленных проблем связано с потерей точности внутренних вычислений.

Контролировать точность, используя стандарт- ные вещественные типы данных, предлагаемые большинством распространенных языков програм- мирования, весьма сложно. Большинство современ- ных компьютеров поддерживают стандарты ANSI представления вещественных чисел, однако даже 10-байтовый тип extended позволяет хранить не бо- лее 20 значащих цифр. В то же время при описании 6-й задачи показано, что для корректных вычисле- ний требуется 4n-значная арифметика. Это означа- ет, что реальная достижимая точность построения триангуляции Делоне составляет не более 20 / 4 = 5 знаков в задании координат исходных данных. Т.е. значение точности ε для проверки совпадения двух точек, возникшее при описании 1-й задачи, следует

установить не менее чем 10−5 , что не всегда прием- лемо на практике.

Другойспособзаключаетсявиспользованиивявном виде вычислений с фиксированной точкой. В этом слу- чаеможноточноконтролироватьвсепотериточности.

Еще проще является переход к целочисленному представлению координат исходных точек. Напри- мер, используя обычные 32-битные целые числа, можно обеспечить точность представления в 9 зна- чащих цифр, что является уже приемлемым в боль- шинстве ситуаций. Тогда для реализации алгоритма построения триангуляции понадобится реализовать несколько дополнительных функций, оперирующих с 32-, 64- и 128-битными числами. Выполненная на платформе IA-32 автором реализация алгоритма включала в себя следующие функции:

1.Mul64(A,B). Умножение 32-разрядных чисел. Результат возвращается 64-разрядным. Функция реализована как одна команда ассемблера.

2.Sqr64(A). Возведение 32-разрядного числа в

квадрат. Результат возвращается 64-разрядным. Функция реализована как одна команда ассемблера.

3.MulSum64(A,B,C,D). Сумма двух произведений 32-разрядных чисел A⋅B и C⋅D. Результат возвраща- ется 64-разрядным. Функция реализована с помо- щью 9 команд ассемблера.

4.MulDif64(A,B,C,D). Разность произведений 32-

разрядных чисел A·B и C·D. Результат возвращается 64-разрядным. Функция реализована с помощью 11 команд ассемблера.

5.Mul128(A,B). Умножение 64-разрядных чисел. Результат возвращается 128-разрядным. Функция реа- лизованаспомощью40 командассемблера.

6.Compare128(A,B,C,D). Вначале вычисляется сум-

ма двух произведений 64-разрядных чисел A·B и C·D.

Затемполучаемое128-разрядноечислосравниваетсяс нулем. Если оно меньше нуля, то возвращается false, иначе – true. Функция реализована с помощью двух вызововфункцииMul128 идополнительных13 команд ассемблера.

(Использование 64-битных микропроцессоров могло бы существенно сократить реализацию до 1– 4 команд ассемблера для каждой функции.)

Таким образом, используя целочисленный способ представления исходных данных совместно с допол- нительными операциями над 32-, 64- и 128-битными целымичислами, можнорешитьпоставленныезадачи.

Если используются целочисленные вычисления, то отпадает необходимость использования величин ε, возникающих в задачах 1 и 3, и можно выполнять проверки на равенство непосредственно.

Рассмотрим описанную в 8-й задаче проблему поиска точек пересечения и разбиения вставляемых структурных ребер на части.

Несмотря на то, что мы можем выполнять вычис- ления с помощью дополнительных функций практи- чески без потери точности, все равно точка пересе- чения двух прямых в общем случае будет иметь не- целые координаты, которые мы будем вынуждены округлить, т.е. в общем случае точка пересечения двухпрямыхнебудетлежатьнаэтихпрямых.

Встает необходимость модификации алгоритма вставки структурных линий так, чтобы учесть воз- можные нарушения структуры триангуляции и из- бавиться от них. Автором предлагается следующий алгоритм вставки структурных линий.

Алгоритм вставки структурных линий в три- ангуляциюсограничениями. ПустьL – сортирован-

ный по длине список еще не вставленных отрезков структурных линий. Вначале в L заносим все отрезки исходных структурных линий. Пока список L не пуст, извлекаем (с удалением) из этого множества самый длинный отрезок AB. Далее пытаемся вставить этот отрезок в триангуляцию методом, описанным в [3]. Если обнаруживается, что вставляемый отрезок пере- секает некоторые ранее вставленные структурные ребра, то их необходимо удалить из триангуляции. При этом надо найти все точки пересечения Ci, где

i =1, n , новогоотрезкасовставленнымиребрамиEiFi. Затем надо в список L поместить все отрезки CiCi+1, где i =0, n, C0=A, Cn+1=B. Также необходимо туда

поместить все отрезки EiCi и CiFi, где i =1, n . Если

вставляемый в список отрезок имеет нулевую длину, тоневставляемего. Конецалгоритма.

Впроводимом авторомисследованииданногоалго- ритма достаточно часто возникала ситуация, когда не- большое количество исходных структурных линий приводиткзначительномуразрастаниюспискаL впро- цессе работы. Например, задав 5 «почти» коллинеар- ных отрезков в качестве исходных структурных линий, алгоритмвконцеконцоввыдавалболее15 тысячструк- турных ребер. Происходит это вследствие того, что каждая пара отрезков после нахождения их пересе- чений образует 4 новых отрезка, также являющихся «почти» коллинеарными остальным отрезкам. Такое дробление идет до тех пор, пока размеры отрезков не станут сравнимыми с размерами единицы координат-

93

нойсетки, когдамаленькиеотрезкистановятся«совсем не» коллинеарными или размер отрезков становится настолько малым, что его дальнейшее деление невоз- можно. Но и на этом микроуровне возможны пробле- мы. Например, пусть построена некоторая «плотная» триангуляция, когдавкаждомузлекоординатнойсетки имеется по узлу триангуляции и требуется вставить отрезокAB, которыйпересекается сранеевставленным структурным ребром CD (рис. 3). В результате найден- ная точка пересечения AB и CD будет округлена, на- пример, доточкиA. ВитогевсписокL попадутотрезки AC, AD и опять AB. Так как мы извлекаем на каждом шаге из списка самое большое ребро, то он будет бес- конечно разрастаться за счет постоянной вставки ребер

AC иAD.

Таким образом, в этом варианте алгоритм все же не годится для практической работы.

Рис. 3. Попытка вставки микроребра

Во избежание пересечения пар «почти» колли- неарных отрезков и проблем на микроуровне авто- ром предлагаются две модификации алгоритма.

Во-первых, при вставке очередного отрезка не- обходимо найти все узлы триангуляции, лежащие

вблизи от отрезка на расстоянии не более некоторо- го ε1. Тогда, если такие точки найдены, вставляе- мый отрезок разобьем этими точками на части, ко- торые поместим в список L.

Во-вторых, найдя точку пересечения структурных ребер, прежде чем вставлять новый узел, попробуем найти в окрестности радиуса ε2 другой, ранее уже вставленныйузелтриангуляции.

В проведенном автором экспериментальном моде- лированииработыалгоритмазначительноеулучшение наблюдалось уже при значениях ε≥3. Увеличение ε приводит к сокращению размера списка L, но не- сколько увеличивает время выполнения дополнитель- ного поиска точек в окрестностях. Экспериментально были выбраны наиболее приемлемые с точки зрения быстродействияикачествазначенияε1=ε2=10.

Заключение

Использование целочисленного представления ис- ходных чисел позволяет, с одной стороны, явно кон- тролировать точность вычислений, с другой – повы- сить скорость работы алгоритма построения триангу- ляциизасчетотказаотвещественныхопераций.

Темнеменеепростойпереходотвещественныхвы- численийкцелочисленным приводиткдругомунепри- ятному эффекту – значительному росту количества структурных ребер в триангуляции. Во избавление от этогоприходитсянесколькоусложнятьалгоритм, вводя дополнительные проверки на наличие совпадающих узловтриангуляциисзаданнойточностьюε.