УДК 004.942

Г. С. Евсеев

кандидат технических наук, доцент

О. С. Лесникова

Санкт-Петербургский государственный университет аэрокосмического приборостроения

МОДЕЛЬ ВЗАИМОДЕЙСТВИЯ ПОТОКОВ ТРАНЗАКЦИЙ НА SQL-СЕРВЕРЕ

Аннотация

В данной статье рассматривается модель взаимодействия двух потоков транзакций на SQL-сервере с учетом действия механизма блокировок.

Abstract

The transaction streams interaction model in the SQL server is considered. This model takes into account mechanism of transactions isolation as in standart ANSI SQL-92.

Введение

В настоящее время широко используются реляционные СУБД, ядром которых является SQL-сервер, обслуживающий запросы множества пользователей к базе данных [1]. Вместе с тем, предсказание характеристик качества обслуживания во многих случаях наталкивается на серьезные трудности и требует большого числа экспериментов. Это связано с тем, что функционирование SQL-сервера существенно сложнее моделей, рассматриваемых в традиционной теории массового обслуживания [2]. Здесь исследуется один из вариантов обобщения известных моделей, что позволяет учесть некоторые существенные особенности SQL-сервера.

Описание модели

Одной из главных особенностей SQL-сервера является возможность как последовательного, так и параллельного выполнения транзакций. Как следует из описания стандарта языка SQL [3], возможны три модели взаимодействия двух транзакций:

— модель «BB». Транзакции Тр1 и Тр2 выполняются последовательно в порядке поступления;

— модель «BN». Если первой начинает выполняться транзакция Тр1, то транзакция Тр2 может начать выполнение только после завершения транзакции Тр1. Если же первой начинает выполняться транзакция Тр2, то транзакции Тр1 разрешено начать выполнение по мере готовности, не дожидаясь завершения транзакции Тр2;

— модель «NN». Каждая из двух транзакций может начать выполнение по мере готовности, не дожидаясь завершения конкурирующей транзакции.

Для уточнения моделей «BN» и «NN» следует определить, как влияет на скорость выполнения транзакции параллельное выполнение другой транзакции. В теории массового обслуживания для систем с параллельным обслуживанием заявок известны две модели.

В первой модели предполагается, что для выполнения второй заявки выделяется дополнительный сервер, в результате чего скорость выполнения первой заявки не изменяется, и заявки выполняются независимо.

Во второй модели (модель разделения процессора) предполагается, что ресурс процессора делится поровну между заявками, в результате чего скорость выполнения каждой из них уменьшается вдвое.

Обе модели очевидным образом обобщаются на любое число выполняемых параллельно заявок, но ни одна из них не является достаточно адекватной для описания SQL-сервера. Ближе к реальности модель с конечным числом серверов в системе. При этом, пока число параллельно выполняемых транзакций не превосходит числа серверов, скорость выполнения транзакций не уменьшается, а затем она начинает уменьшаться и стремится к величине, равной отношению числа серверов к числу параллельных транзакций. В общем случае, будем полагать, что при параллельном выполнении k транзакций скорость их выполнения уменьшается в (G/k) раз, где G — число из интервала от 1 до k включительно. Ясно, что значение G связано с уровнем общей загрузки SQL-сервера.

Теоретический анализ модели

Будем полагать, что на вход системы массового обслуживания (СМО), содержащей два бесконечных буфера, поступают соответственно два независимых пуассоновских потока заявок, для каждого из которых время обслуживания имеет экспоненциальное распределение вероятностей и не зависит от других случайных величин в системе. Заявки каждого потока обслуживаются последовательно в порядке поступления.

Пусть λ1, λ2 и μ1, μ2 обозначают интенсивности поступления и соответственно интенсивности обслуживания потоков, а T1 и T2 обозначают среднее время задержки в СМО заявок первого и соответственно второго потока. Требуется оценить значения T1, T2 через исходные величины.

Введем следующие обозначения.

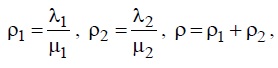
где ρ1, ρ2, ρ — коэффициенты загрузки системы для первого потока, второго потока и суммарный коэффициент соответственно.

Очевидно, для устойчивой работы системы необходимо выполнение условия ρ <1.

Модель «BB»

Для этой модели доопределим процедуру обслуживания буферов следующим образом. Если оба буфера не пусты, то при освобождении сервера из двух заявок выбирается та, которая пришла раньше. При этом рассматриваемая система сводится к системе с пуассоновским входным потоком заявок интенсивности (λ1+λ2), для которых распределение вероятностей времени обслуживания является смесью экспоненциальных распределений с параметрами μ1 и μ2. Тогда среднее время пребывания заявки в буфере вычисляется по формуле Поллачека-Хинчина:

где m и t2 вычисляются по следующим формулам:

и исследуемые величины вычисляются по формулам

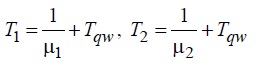
Модель «BN»

Для этой модели будем называть заявки первого потока блокирующими, а заявки второго потоканеблокирующими. Тогда процедура выбора заявок на обслуживание описывается следующим образом.

Очередная блокирующая заявка поступает на обслуживание либо по мере готовности (если завершено обслуживание предыдущей блокирующей заявки), либо после завершения обслуживания предыдущей блокирующей заявки.

Очередная неблокирующая заявка поступает на обслуживание либо по мере готовности (если в этот момент не обслуживается блокирующая заявка и завершено обслуживание предыдущей неблокирующей заявки), либо после завершения обслуживания предыдущей неблокирующей заявки (если в этот момент не обслуживается блокирующая заявка), либо после завершения обслуживания блокирующей заявки (если к этому моменту завершено обслуживание предыдущей неблокирующей заявки).

Из приведенного описания следует, например, что при наличии очередей в обоих буферах блокирующие заявки будут поступать на обслуживание сразу после завершения обслуживания предыдущей блокирующей заявки, а неблокирующая заявка будет ожидать не только завершения обслуживания предыдущей неблокирующей заявки, но и ближайшего момента завершения обслуживания блокирующей заявки.

Теперь будем полагать, что при одновременном выполнении блокирующей и неблокирующей заявок интенсивности их обслуживания (mu1 и mu2) умножаются на коэффициент G, принимающий значение из интервала [0.5, 1]. Отметим, что крайние значения интервала соответствуют двум известным моделям параллельного обслуживания заявок.

Для данной модели несложно провести приближенный анализ только для некоторых частных случаев.

Введем следующее допущение: μ2>>λ1, λ2, μ1. Из этого условия сразу следует, что второй поток заявок практически не влияет на обслуживание заявок первого потока, т.к. параллельно с обслуживанием блокирующей заявки обслуживается не более одной неблокирующей заявки. Таким образом,

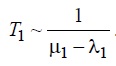
Для оценки величины T2 введем дополнительное ограничение на соотношение интенсивностей двух потоков.

>λ2 буфер второго потока будет с большой вероятностью содержать не более одной заявки, которая либо сразу поступит на обслуживание, либо будет ожидать завершения обслуживания блокирующей заявки. При этом

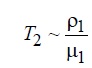
При λ1 <<λ2 буфер второго потока будет с высокой вероятностью содержать большое число заявок, и в среднем неблокирующие заявки будут ожидать освобождения первого буфера. При этом

Теперь предположим, что μ1>>λ1, λ2, μ2. В этом случае обслуживание первого потока практически не влияет на характеристики обслуживания второго потока. Следовательно,

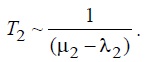
Величина T1 определяется в основном временем обслуживания блокирующих заявок, а распределение вероятностей для этого времени является смесью двух экспоненциальных распределений с параметрами μ1 и (Gμ1). Из этого следует, что

Модель «BN»

В этой модели предполагается, что очередная заявка из каждого буфера поступает на обслуживание, не ожидая завершения обслуживания заявки из конкурирующего потока, но при параллельном выполнении двух заявок интенсивность обслуживания каждой из них умножается на коэффициент G, введенный в описании модели «BN» . Точный анализ величин T1 и T2 пока не выполнен, но в одном частном случае несложно получить приближенные формулы.

Пусть выполнено неравенство μ1>>λ1, λ2, μ2. При этом условии величины T1 и T2 оцениваются приближенно по тем же формулам, что и для модели “BN” .

Результаты моделирования

При моделировании характеристики двух потоков задавались одинаковыми, и исследовалась зависимость величин Т1 и Т2 от суммарной загрузки системы R. По виду этой зависимости можно судить о том, насколько блокировки увеличивают время выполнения транзакций.

На рис. 1 представлены графики зависимостей для случая, когда предлагаемая модель совпадает с моделью разделения процессора, т.е. G=0.5. Из графиков видно, что влияние блокировок на исследуемые величины относительно мало, т.е. использование механизма разделения транзакций в SQL-сервере малоэффективно.

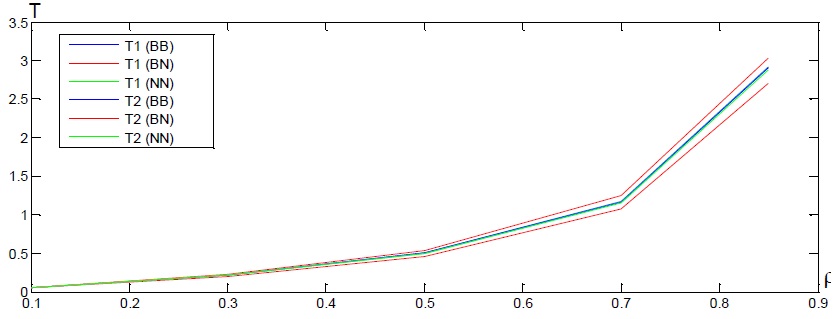
Рис. 1. Графики зависимостей при G=0.5

На рис. 1 представлены графики зависимостей для случая, когда при параллельном выполнении двух заявок скорость их выполнения не уменьшается, т.е. G=1. При этом, как показывают графики, обслуживание заявок при наличии блокировок существенно (в несколько раз) может замедлить обслуживание транзакций. Причем, с увеличением общей загрузки сервера величина замедления возрастает. В этом случае использование уровней разделения транзакций на SQL-сервере позволяет существенно увеличить его производительность при сохранении целостности данных.

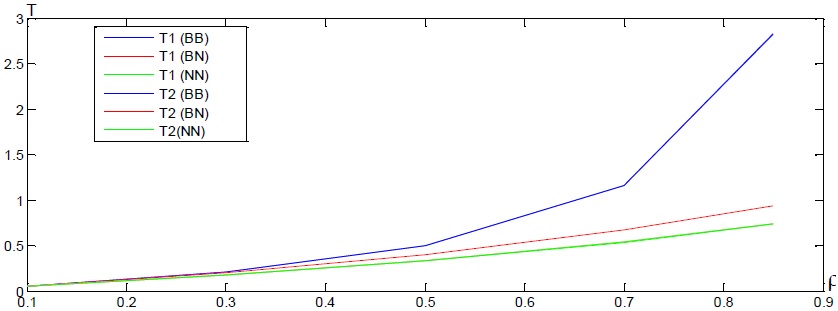
Рис. 2. Графики зависимостей при G=1

Заключение

Выполненное исследование позволяет сделать следующий вывод. Механизм разделения транзакций на SQL-сервере эффективен лишь тогда, когда сервер не перегружен, т.е. выделение ресурсов для нового поступившего запроса не уменьшает ресурсы для обрабатываемых запросов.

В дальнейшем представляет интерес обобщение предложенной модели более чем на два потока транзакций, а также рассмотрение случая, когда в каждом потоке могут встречаться и блокирующие, и неблокирующие транзакции.

Библиографический список

1. Крис Дж. Дейт. Введение в системы баз данных / Крис Дж. Дейт; Москва, Вильямс, 2006. 1328 с.

2. Donald Gross. Solutions Manual to Accompany Fundamentals of Queueing Theory, Fourth Edition / Donald Gross, John F. Shortle, James M. Thompson, Carl M. Harris; Wiley-Interscience, 2008. 88 p.

3. Стандарт ANSI SQL-92; 1992. 624 с.