Построение математической модели эмоций

Объектом рассмотрения настоящей работы являются эмоции человека. Вопрос рассмотрения эмоций и практического применения знаний о них все чаще встает в с самых разных сферах нашей жизни [1,2]. Основные задачи статьи – это определение основных понятий, характеристик, функций из теории эмоций и построение математической модели эмоции (эмоционального тона).

В современной теории эмоций положительные и отрицательные эмоции трактуются как противоположные и человек, в каждый данный момент, может находиться либо в радостном, либо в грустном эмоциональном состоянии [3]. Корреляция между положительными и отрицательными либо обратная, либо близка к нулю. Зависимость между ними однозначно не установлена, но возможными критериями оценки такой зависимости могут быть: возраст, личностные особенности, социальный статус, и другие. Однако многие авторы отмечают и наличие сложных эмоций, что в свою очередь противоречит первому утверждению [2,3]. Конечно же, такое деление во многом условно. Например, страх (традиционно считающийся отрицательной эмоцией) имеет положительную составляющую и может приносить удовольствие. А радость может проявляться в форме злорадства, принося такой же вред, как и гнев. Поэтому чтобы устранить неоднозначность трактовок положительных и отрицательных эмоций введем следующее разделение. Будем говорить, что существуют эмоции, способствующие повышению психологической энтропии (отрицательные), и эмоции, наоборот, улучшающие конструктивное поведение (положительные). При этом под оценкой конструктивного поведения будем понимать выполнение или не выполнение некоторого ранее намеченного действия.

Характеристиками эмоционального реагирования являются:

1. интенсивность – глубина переживаний и величина физиологических сдвигов.
2. длительность протекания - от мимолетных переживаний до состояний длящихся несколько часов (дней).
3. предметность - степень осознанности и связи с конкретным объектом и ситуацией. Все эмоциональные реакции имеют определенный предмет. Непредметные реакции имеют под собой менее определенный предмет.
4. влияние на поведение и деятельность (стимулирующее или тормозящее)
5. модальность – качественная специфика эмоционального реагирования. Означает, что в отношении того или иного предмета возникнет определенно направленная эмоциональная реакция. Например, при достижении цели – радость, при недостижении – разочарование, в опасной ситуации – страх.
6. знак – положительные и отрицательные эмоции (сильнее выражены).
7. реактивность – быстрота возникновения или изменения.
8. качество – связь с потребностью.
9. степень произвольного контроля.

Эмоциональное реагирование делится на:

1. кратковременные эмоции
   • эмоциональный отклик – динамично изменяющееся состояние, не изменяющее эмоциональное состояние – пример, эмоциональное реагирование спортсменов в процессе игры.
   • эмоциональная вспышка – изменяет эмоциональное состояние, обладает большей интенсивностью.
   • эмоциональный взрыв – кратковременная бурно развивающаяся реакция, изменяющая эмоциональное состояние с подавлением волевого контроля.
2. эмоциональное состояние – длительное, устойчивое состояние (настроение, эмоциональное поведение).
3. Эмоциональный тон

Эмоциональный тон – это характерное реагирование на отдельные свойства объектов или явлений (приятный или неприятный запах, звук, сочетание цветов). [3]

Функциями эмоционального тона являются:

1. Ориентировочная – состоит в сообщении организму, опасно или нет то или иное воздействие, желательно ли оно, или от него надо избавиться. По П.К.Анохину, это «пеленги» полезности или вреда, устойчиво сохраняющиеся на протяжении миллионов лет [4].
2. Обратная связь – сообщает человеку, что имеющаяся биологическая потребность удовлетворена (эмоциональный тон - удовольствие) или не удовлетворена (эмоциональный тон – неудовольствие).
3. Регулирующая – состоит в необходимости проявления определенных видов поведения до тех пор, пока не будет достигнут нужный организму результат. Учтем здесь и торможение некоторого поведения, то, что раньше приносило удовольствие, может вызвать отвращение.

Эмоциональный тон со временем может меняться (дети ненавидят лук, взрослые уже могут его есть). Так же важным является сила раздражителя (то, что при слабом давлении приятно, при сильном вызывает неприязнь). Многократное повторении положительных оценок ведет к их нейтрализации.

Определим понятие эмоции. Под эмоцией будем понимать переживание человеком в данный момент своего отношения к чему-либо. Эмоция – это рефлекторная адаптивная психофизиологическая реакция, связанная с проявлением субъективного пристрастного отношения (в виде переживаний) к значимой ситуации и ее исходу и способствующую организации и обеспечению целесообразного с точки зрения целостности и сохранности организма поведения человека [3]. Эмоции характеризуются отчетливо выраженной интенсивностью (достаточно сильно выраженное переживание человеком горя, радости); ограниченной продолжительность (эмоция длится относительно недолго, ее продолжительность ограничена временем непосредственного действия причины или временем воспоминания о ней); хорошей осознаваемостью причины ее появления; связью с конкретным объектом, обстоятельством; полярностью (радость и печаль, гнев и страх).

Эмоция намного более высокий в эволюционном развитии уровень эмоционального реагирования, чем эмоциональный тон. Эмоция – это адаптивная реакция на ситуацию, а не на определенный раздражитель. (Ребенок начинает радоваться не когда он начинает есть конфету, а когда он ее получил). Эмоциональный тон приводит к эмоции, но эмоция возникает при оценке ситуации (боль – грозит неприятностями, которые необходимо будет преодолевать). Эмоции – это дифференцированная оценка разных ситуаций. Эмоциональный тон дает обобщенную оценку, эмоция более тонко показывает значение той или иной ситуации. Эмоции – это не только способ оценки предстоящей ситуации, но и механизм заблаговременной и адекватной подготовки к ней за счет мобилизации психической и физической энергии. Эмоция, как и эмоциональный тон, выступает как механизм предвидения значимости для человека той или иной ситуации. Эмоция, как и эмоциональный тон, механизм закрепления положительного и отрицательного опыта (положительное или отрицательное подкрепление деятельности).

Учитывая, что на практике очень сложно объективно оценить эмоции человека в силу отсутствия априорной информации о ситуации, в которой находится человек, а так же субъективности такой оценки, упростим понятие эмоции, принимая за эмоцию эмоциональный тон ощущений.

Построим модель эмоций. Рассмотрев различные подходы к построению моделей (классический логический подход, нечеткая логика, нейронные сети, имитационное моделирование) и проанализировав возможности их применения для построения модели эмоций, был сделан вывод, что наиболее подходящим аппаратом для описания модели эмоций будет аппарат иммунных систем [5-8]. При этом математическая модель строится на основе соотношения баланса для каждого из компонентов, участвующих в возникновении и протекании эмоции. Именно ввиду такой концепции частные особенности эмоций не существенны для анализа динамики развития эмоции, а на первый план выступают основные закономерности протекания эмоции. Ограничимся рассмотрением трех компонент: объекта вызывающего эмоции (стимула), знаний об объекте вызывающего эмоции (описание того, как нужно противодействовать стимулу) и способностей к обучению (позволяющих получать знания о стимуле). Рассмотрим процесс возникновения и протекания эмоции. Пусть в некоторый момент времени t0 человеку был предъявлен некоторый стимул. Действие стимула приведет к возникновению эмоции, т.е. переходу человека из некоторого нормального для него состояния в измененное под действием стимула состояние. Для минимизации этого эффекта и возврату в нормальное состояние человеку требуются знания о действии стимула. Если стимул был предъявлен впервые, то происходит обучение, т.е. повышение количества знаний о стимуле, и время протекания эмоции (t) достаточно велико. Если стимул уже предъявлялся, то действие стимула, либо полностью игнорируется, либо человек возвращается в нормальное состояние значительно быстрей. При этом стоит учесть, что при длительном непредъявлении некоторого стимула происходит угасание знаний о нем. Таким образом, эмоция является механизмом поддержания некоторого состояния (нормального для данного человека). Следует также отметить, что при протекании эмоции большое значение имеет степень воздействия стимула, силы его действия и состояния в котором находится человека (т.е. насколько сильно на него уже подействовал стимул), поскольку это в конечном итоге приводит к снижению активности защиты человека. Это, естественно, должно быть отражено в математической модели.

Основными действующими факторами эмоции являются следующие величины:

1. Количество предъявленных объектов вызывающих эмоцию V(t).
2. Количество знаний об объектах вызывающих эмоции (наша защита) F(t). Под знаниями понимаются знания, нейтрализующие действие объектов вызывающих эмоции.
3. Общий размер наших знаний C(t). Сюда входят все знания об объекте вызывающем эмоции. Отражает наши уникальные способности к обучению.
4. Наступление эмоции (относительная характеристика человека испытывающего эмоцию) m(t).

Модель эмоций представим в виде системы дифференциальных уравнений. Составим первое уравнение, оно будет описывать изменение количества предъявления стимула, вызывающего эмоции.

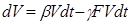
Первый член в левой части этого уравнения описывает прирост объектов вызывающих эмоции dV за интервал времени dt. Естественно, что он пропорционален V и некоторому числу ?, которое будем называть коэффициентом появления стимулов. Член ?FVdt описывает число стимулов, нейтрализуемых знаниями F за интервал времени dt. В самом деле, число таких стимулов, очевидно, будет пропорционально как количеству знаний об объектах вызывающих эмоции, так и числу стимулов; ? - коэффициент, связанный с вероятностью нейтрализации стимула знаниями о стимуле. Разделив (1) на dt получим

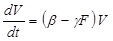
Переходим к построению второго уравнения, которое будет описывать рост знаний об объекте. В нашей модели под знаниями о стимуле понимаются знания, защищающие нас от стимула, и тогда увеличение знаний от встречи со стимулом, будет пропорционально VF. Таким образом, приходим к соотношению, описывающему прирост знаний (возмущения) над нормальным уровнем C* - постоянным уровнем знаний (возмущения) в здоровом организме:

Первый член в правой части описывает генерацию возмущения, ? - время, в течение которого осуществляется формирование знаний о стимуле, ? - коэффициент, учитывающий вероятность соответствия знаний - стимулу, возбуждение реакции и число образующихся новых знаний. Второй член в этой формуле описывает уменьшение числа знаний за счет старения, ?c - коэффициент, равный обратной величине их времени жизни. Разделив (3) на dt получим:

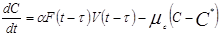
Для получения третьего уравнения подсчитаем баланс числа знаний, реагирующих со стимулом. Будем исходить из соотношения

Первый член справа рСdt описывает генерацию знаний (защиты) об объекте знаниями за интервал времени dt, ? - скорость производства знаний о стимуле. Второй член ?yFVdt описывает уменьшение числа знаний о стимуле в интервале времени dt за счет связи с самими стимулами. В самом деле, как было отмечено выше при выводе уравнения, количество выбывающих за интервал времени dt стимулов за счет нейтрализации их знаниями о стимуле было равно yFVdt. Если на нейтрализацию одного стимула требуется ? знаний, то мы и приходим к указанному члену формулы. Третий член описывает уменьшение количества знаний за счет старения, где ?f - коэффициент, обратно пропорциональный времени исчезновения знаний. Разделив (5) на dt получим

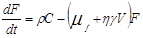
Построенные уравнения не учитывают ослабления тонуса организма в ходе переживания эмоций, связанного с уменьшением активности поставки знаний (распознавателей), необходимых для борьбы с появляющимися стимулами. Примем гипотезу о том, что переживание эмоции связано с размерами поражения стимулами. С этой целью введем в рассмотрение уравнение для относительной характеристики поражения. Пусть M - характеристика нормального состояния, а M' - соответствующая характеристика нормального состояния человека на которого уже начал действовать стимул. Введем в рассмотрение величину m по формуле

Это будет относительная характеристика поражения человека эмоцией. Для нормального состояния она, естественно равна нулю, а для полностью пораженного - единице. Для этой характеристики рассмотрим уравнение

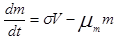
Первый член в правой части характеризует степень поражения органа. Предполагается, что за интервал времени dt увеличение относительной величины пораженного органа пропорционально количеству стимулов, которое описывается членом ?V, где ? - некоторая константа, своя для каждой эмоции. Уменьшение этой характеристики происходит за счет восстановительной деятельности организма. Этот член будет зависеть от m с коэффициентом пропорциональности ?m, характеризующим обратную величину периода восстановления органа в m раз.

Совершенно ясно, что при сильном поражении, т.е. при большом отклонении от нормального состояния производительность обучения падает. Это является роковым для человека и ведет к затяжным психологическим заболеваниям. В нашей модели фактор поражения жизненно важных органов можно учесть в уравнении два, заменив коэффициент ? на произведение ??(m). В реальных условиях график ?(m) может иметь сложную форму, но качественно он всегда будет состоять из постоянной ? = 1 в начале изменения аргумента m и убывающей, по линейной или нелинейной зависимости при дальнейшем увеличении этого аргумента.

Таким образом, получили систему дифференциальных уравнений, описывающих протекание эмоции

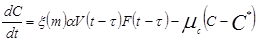
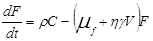
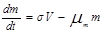
Обычно для уравнений с запаздыванием начальные условия задаются на интервале [t0-?, t0]. Однако в силу принятых нами ограничений до момента предъявления стимула t0 эмоций не было: V(t)==0 при t < t0, и поэтому начальные условия можно задать в точке t0. Тогда начальные условия будут заданы в виде V(t0) = V0, C(t0) = C0, F(t0) = F0, m(t0) = m0. При этом V0 >= 0, C0 >= 0, F0 >= 0, m0 >= 0.

Для определения начальных значений может быть использован подход предложенный в [2,8].

Предложенная модель имеет не только теоретический интерес, но и практическую направленность. Рассмотрение процесса протекания эмоции и прогнозирование того, на сколько долго будет находиться человек в том или ином эмоциональном состояний может быть применено во многих областях жизнедеятельности человека, в частности в маркетинговых исследованиях, в рамках построения человеко-компьютерных интерфейсов, в робототехнике.

Список использованной литературы

1. Заболеева-Зотова А.В. The Emotional Oriented Interface Software Researching// Interactive Systems: The Problems of Human-Computer Interaction. Proceedeng of the Interactionol Conference (September 23-27 2001). - Ulianovsk, 2001.
2. Розалиев В.Л. Предпосылки, возможности, перспективы создания автоматизированной системы распознавания эмоциональности речи// Известия Волгоградского государственного технического университета: межвузовский сборник научных статей. – 2008. – №2(40). – С.58-61
3. Ильин Е.П. Эмоции и чувства. 2-е изд. – СПб.: Питер, 2008.
4. Анохин П.К. Узловые вопросы теории функциональной системы. - М.: Наука, 1980.
5. Заболеева-Зотова А.В Естественный язык в автоматизированных системах. Семантический анализ текстов. Монография. - Волгоград: ВолгГТУ, 2002.
6. Искусственные иммунные системы и их применение/ Под ред. Д. Дасгупты. Пер. с англ. – М.: Физматлит, 2006.
7. Марчук Г.И. Математические модели в иммунологии// Вычислительные методы и эксперименты. Вып.3. - М.: Наука, 1991.
8. Розалиев В.Л. Построение модели эмоций по речи человека// Известия Волгоградского государственного технического университета: межвузовский сборник научных статей. – 2007. – №9(35). – С.62-65