
Авторы: О.В. Бузулёв, А.С. Болотов, В.А. Куевда, П.И. Розкаряка
Руководитель: к.т.н., доц. Розкаряка П. И.
Источник: III Международная научно-практическая конференция Инновационные перспективы Донбасса, ДонНТУ, 2017 г.
В статье рассмотрены вопросы идентификации параметров двигателя по имеющимся экспериментальным данным. Для этого используется функция Parameter Estimation математического пакета Matlab. Такой способ дает возможность легко определить ранее неизвестные параметры объекта регулирования, необходимые для качественной настройки электромеханической системы.
Для качественной настройки современных электромеханических систем необходимо как можно точнее знать параметры объекта регулирования. Однако данные параметры не всегда являются известными. Зачастую мы имеем лишь структуру модели, не зная точного математического описания, и, чаще всего, имеем возможность получить реальные данные в виде осциллограмм переходных процессов, т.е. так называемую модель по типу «серого ящика».
Для определения параметров объекта регулирования можно воспользоваться функцией Parameter Estimation математического пакета Matlab/Simulink. Для того чтобы воспользоваться данной функцией необходимо иметь экспериментальные данные и структуру модели с искомыми параметрами.
Рассмотрим пример использования указанной функции применительно к такому объекту регулирования как двигатель постоянного тока. Для определения параметров двигателя была построена модель, представленная на рис. 1. В данной схеме DC Motor–модель двигателя постоянного тока, Rotational Friction–блок имитации момента трения во вращающемся механизме, Ideal Rotational Motion Sensor–идеализированный датчик вращения вала двигателя, Current Sensor–датчик тока,Controlled Voltage Source–управляемый источник напряжения, TP–тиристорный преобразователь, From Workspace–блок считывания данных из рабочего пространства Matlab. В модели присутствуют блоки как из библиотеки Simulink, так и из Power Systems.
В модели будут идентифицироваться следующие параметры–сопротивление и индуктивность якорной цепи, конструктивная постоянная двигателя, момент инерции и момент трения в механизме.
Экспериментальные данные были получены на лабораторном стенде, находящемся в лаборатории 8109 кафедры ЭАПУ. Для идентификации параметров двигателя были взяты осциллограммы тока якоря и скорости вращения двигателя. Заданием для модели является тот же самый сигнал, который был использован для получения экспериментальных данных.

Рис. 1 – Модель подготовленная для использования функции Parameter Estimation
Для идентификации параметров воспользуемся функцией Parameter Estimation. Данная функция позволяет производить оценку параметров модели в Simulink, используя экспериментально полученные данные и переменные в самой модели. Можно оценивать несколько параметров сразу, при этом можно устанавливать границы их изменения. Вид окна функции Parameter Estimation изображен на рис. 2. В приведенном на рисунке случае оценка параметров уже осуществлена. На двух средних графиках приведены экспериментальные осциллограммы и работа модели, на правом графике – количество итераций и изменение варьируемых параметров.
Изначально в модель были заложены основные параметры двигателя, обозначенные в виде переменных, которые при помощи функции Parameter Estimation и будут идентифицированы.
На рис. 3 и 4 изображены графики скорости и тока якоря двигателя, полученных экспериментально, и результаты, полученные с помощью модели с начальными параметрами. На рис. 5 и 6 – с идентифицированными параметрами с помощью функции Parameter Estimation соответственно. Несовпадение графиков на отдельных участках говорит о необходимости учета нелинейностей, присутствующих в реальном объекте регулирования.
Более подробно о настройке и последовательности действий для работы с данной функцией можно узнать в вебинаре, который можно скачать на русскоязычном сайте Matlab [1] после регистрации. Все операции производились в пакете Matlab версии R2016a.

Рис. 2 – Окно функции Parameter Estimation
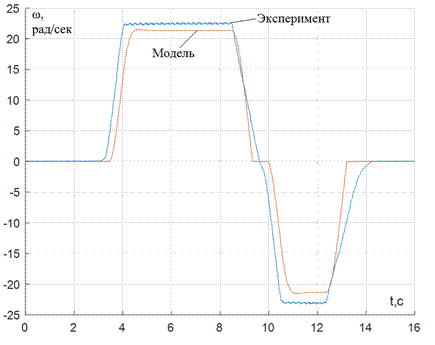
Рис. 3 – График экспериментальных данных (скорости) и работа модели до идентификации параметров

Рис. 4 – График экспериментальных данных (ток якоря) и работа модели до идентификации параметров
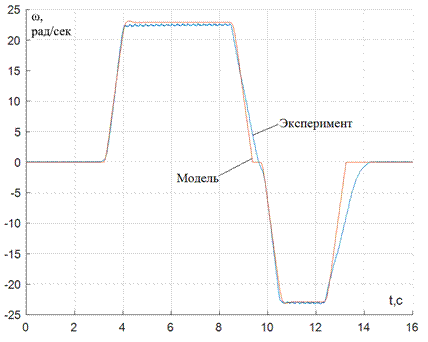
Рис. 5–График экспериментальных данных (скорости) и работа модели после идентификации параметров
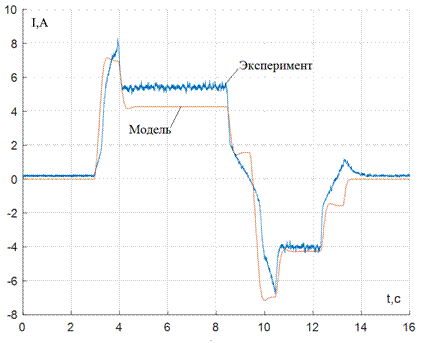
Рис. 6–График экспериментальных данных (ток якоря) и работа модели после идентификации параметров
Анализ полученных результатов подтверждает возможность идентификации параметров и дальнейшего их использования для настройки электромеханических систем. Следует отметить, что точность и соответствие полученных результатов зависит от качества экспериментальных данных.
Для более точной настройки рекомендуется использовать несколько наборов экспериментальных данных и оценить полученные результаты для каждого из них.
Перечень ссылок
1. Вебинар «Проектирование системы автоматического управления электроприводом» [Электронный ресурс] – Режим доступа: http://matlab.ru/webinars/Proyektirovaniye–sistemy–avtomaticheskogo–upravleniya–elektroprivodom/ . – Загл. с экрана. 15 февраля 2017.
2. Mathworks – Оценка параметров модели на основе эксперимента [Электронный ресурс] – Режим доступа: http://matlab.ru/blog/control–algorithms/89/ . – Загл. с экрана. – Дата обновления 12/08/2013.