Высокоскоростная система позиционирования с учетом неизвестного сухого трения и явление насыщения

Аннотация – В традиционной системе позиционирования, когда ошибка позиционирования становится мала, двигатель не может обеспечивать достаточный момент торможения. Следовательно, реакция по положению замедляется.

Существует также другая система позиционирования, суть которой заключается в выходе на задание по положению по трапецеидальной тахограмме скорости. Такая система позиционирования корректна, когда заданы момент нагрузки и конечное положение. Однако, если момент нагрузки и конечное положение варьируются, реакция системы позиционирования не может быть желаемой. Для решения этой проблемы, в данной статье предлагается новая высокоскоростная система позиционирования серводвигателя переменного тока с учетом явление сухого трения и явления насыщения. Предполагается всегда использовать максимальный момент разгона или торможения и максимальную скорость.

1. Введение

В последнее время серводвигатель переменного тока заменяет шаговый двигатель в связи с быстрым развитием однокристальных микрокомпьютеров и DSP в области позиционирования. В сравнении между серводвигателем переменного тока и шаговым двигателями при тех же размерах и условиях, серводвигатель переменного тока имеет более высокий крутящий момент и более высокую эффективность, чем шаговый двигатель. В традиционной системе позиционирования серводвигателя переменного тока, задание скорости определяется посредством разницы между текущим положением и ошибкой позиционирования, при этом задание скорости принимает наименьшее значение вблизи конечной точки позиционирования. Таким образом, получение достаточного момента торможения становится затруднительным, и реакция системы замедляется.

С другой стороны, когда выходной крутящий момент, момент инерции и момент нагрузки серводвигателя известны, оптимальная скорость модели определяется этими данными и задание на положение формируется исходя из тахограммы скорости, в виде S-функции или сплайн функции [1]. Данный метод позволяет обеспечить оптимальное высокоскоростное позиционирование, если задать максимальное ускорение в виде S-образной кривой как задание на положение. Для этого метода управления необходимо знать момент нагрузки серводвигателя. Однако, когда крутящий момент нагрузки изменяется, реакция системы на него также изменяется. Тогда необходимо сформировать задание на положение ещё раз. В этом случае изменится конечная точка позиционирования. Кроме того, зачастую момент нагрузки является неизвестной величиной.

Для решения данных проблем в данной статье предлагается новый алгоритм высокоскоростной системы позиционирования с использованием системы позиционирования и нагрузки в виде сухого трения. В данной статье момент сухого трения оценивается наблюдателем состояния. Эффективность подтверждается результатами численного моделирования и экспериментальными результатами [2].

2. Обычная система позиционирования

Структурная схема обычной системы позиционирования представлена на рис.1. В данной системе контур положение с П-регулятором, а контур регулирования скорости с ПИ-регулятором. Здесь θ_m^ref - задание на положение, θ_m - текущее положение, θ_m^err - ошибка позиционирования, ω_m^ref - задание на скорость, ω_m - текущая скорость, ω_m^err - ошибка по скорость, i_q - крутящий момент (ток), и T_L - момент сопротивления. Частотные характеристики контура регулирования тока обычно выше, чем контура регулирования скорости. Следовательно, выход контура регулирования скоростью становится равным фактическому току i_q. Чтобы выполнить высокоскоростное позиционирование, задание на положение θ_m^ref на рис. 1 должно быть ступенчатым. Исследуемый двигатель представляет собой синхронный двигатель с постоянными магнитами, характеристики которого приведены в таблице I. На рис.2 показана конфигурация экспериментальной системы. Регуляторы положения, скорости и тока построены в системе программного обеспечения сервопривода с помощью DSP (ADMC401).

Таблица I

Характеристики исследуемого двигателя
Номинальная мощность P[W]	90
Номинальное напряжение V[V]	100
Потокосцепление Фfa [Wb]	0.047
Количество пар полюсов p	5
Момент инерции ротора J[kg•m2]	6x10-5
Сопротивление якоря Ra [Ω]	3.08
Индуктивность якоря La[mH]	8.28
Номинальная скорость ωmax [rad/s]	314
Номинальный ток imax [A]	sqrt(3/2)*2
Номинальное напряжение vmax [V]	sqrt(3/2)*70
Импульсный датчик [pulse/rev]	2000

Регулятор положения и регулятор скорости показаны на (1) и (2) соответственно. Частотная характеристика показана на рис. 3. Период дискретности и частота среза этих регуляторов представлены в таблице II. Здесь G_ryθ(s) – это реакция регулятора положения на приложенное воздействие, и она равна дополнительной функции чувствительности T_θ(s). Аналогично G_ryω(s) – это реакция регулятора скорости на приложенное воздействие, и она равна дополнительной функции чувствительности T_ω(s). S_θ (s) – функция чувствительности регулятора положения. S_ω (s) - функция чувствительности регулятора скорости.

Рисунок 1 – Структурная схема обычной системы позиционирования

Рисунок 2 – Конфигурация прототипа

Таблица II – Характеристики исследуемой системы

Регулятор	Положения	Скорости	Тока
Период дискретности	50[μsec]	100[μsec]	1[msec]
Частота среза	40[rad/s]	400[rad/s]	4000[rad/s]

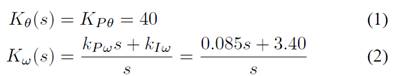
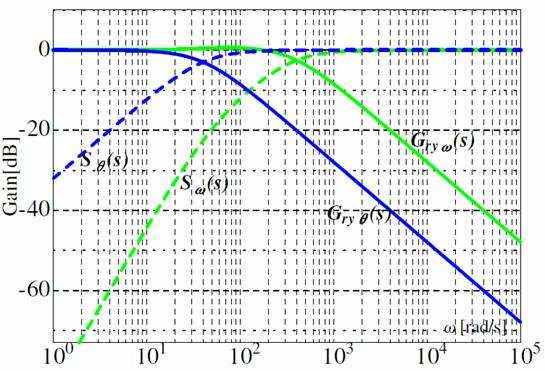
Рисунок 3 – Частотные характеристики

В случае, когда задается большое перемещение, любая позиционная система управления выходит в насыщение. В частности, выход в насыщение происходит во время ускорения или замедления [3]-[7]. В системе управления, показанной на рис. 2, когда выходной сигнал выходит в насыщение, применяется компенсация насыщения, а в обычной системе управления, интегратор ПИ-регулятора прекращает свое действие.

Рисунок 4 и 5 демонстрируют экспериментальные результаты работы обычной позиционной системы. На рисунках 4 и 5 шаг задания на положение равен 6π [rad]. На рисунке 4 представлены графики работы системы без момента сопротивления. На рисунке 5 представлены графики с половинным моментом сопротивления в виде сухого трения, генерируемого системы торможения, изображенной на рисунке 6.

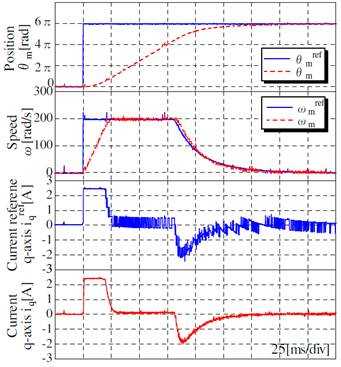
Рисунок 4 – Результаты реакции обычной позиционной системы на скачкообразное задание (без момента нагрузки)

В обоих случаях, во время ускорения система работает с максимальным моментом. Однако во время замедления не используется максимальный крутящий момент. Ошибка по положению в режиме торможения меньше, чем в режиме ускорения. Вследствие чего задание на скорость также мало.

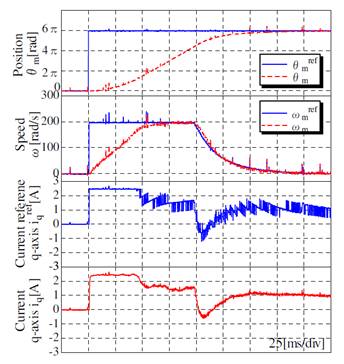
Рисунок 5 – Результаты реакции обычной позиционной системы на скачкообразное задание (с половинным моментом нагрузки)

Рисунок 6 – Система торможения

3. Высокоскоростная позиционная система

На рисунке 7 изображена идеальная осциллограмма для высокоскоростного позиционирования с моментом сопротивления в виде сухого трения. Чтобы выполнить высокоскоростное позиционирование, после режима ускорения необходимо, чтобы серводвигатель работал на максимальной скорости. В конце серводвигатель должен замедляться с использованием максимального крутящего момента.

Чтобы реализовать идеальные задания на скорость и ток двигателя, в этой статье предлагается новый алгоритм генерации опорных сигналов, показанных на рис.7.

Период [t₀, t₂], показанный на рисунке 7, является идеальной реакцией системы, обеспечивающей максимальную скорость ω_max как задание на скорость. Затем, после времени t₂, задание на скорость должно быть нулевым. Затем ток i_q становится равным -i_max, для обеспечения максимального момента торможения. Однако, вычисление времени t₂ в режиме реального времени затруднительно, так как t₂ изменяется в зависимости от задания по положению, либо неизвестно. Соответственно, в данной статье вновь предлагается уравнение (3). Ошибка положения, влияющая на t_2, происходит от сухого трения, оцениваемого наблюдателем состояния, фиксирующего возмущения (наблюдатель возмущений).

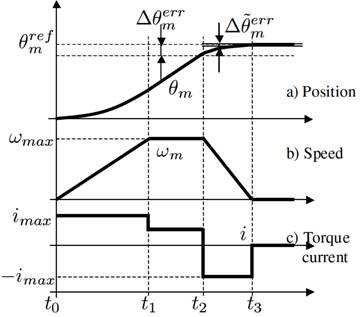
Рисунок 7 – Идеальная осциллограмма высокоскоростной системы позиционирования

Структурная схема предлагаемой системы изображена на рисунке 8. Алгоритм предлагает вычислять Δθ_m^err , используя (3) в предварительном регуляторе, показанном на рисунке 8. Когда текущая ошибка позиционирования θ_m^err становится больше чем Δθ_m^err, максимальная скорость ω_max задается как задание на скорость. В момент времени t₂, когда θ_m^err меньше чем Δθ_m^err, ω_m^ref становится равным нулю. Позже, когда θ_m^err становится меньше чем Δθ_m^err в момент времени t₃, система управления положением переключается с предварительного контроллера, на обычный пропорциональный контур управления положением. Δθ_m^err определяется путем разницы между текущим положением и заданным.

Данная статья позволяет предотвратить явление насыщения с использованием алгоритмов, предложенных в [6], [7], в которых характеристики сервосистемы с замкнутым контуром не изменяются. Предложенный алгоритм компенсации насыщения является цифровым нелинейным алгоритмом. Дискретные уравнения пространства состояния ПИ-регулятора показаны в (4), (5).

Когда выход y регулятора больше предельного значения y_max, y становится равным y_max. Используя разницу между y и y_max, данная статья позволяет предотвратить явление насыщения, вызванное выходным ограничением ПИ-регулятора. Предложенный алгоритм компенсации насыщения для регулятора корректирует переменную состояния x(k + 1) как показано на (6) и (7). Скорректированное ў (k) показано в (8).

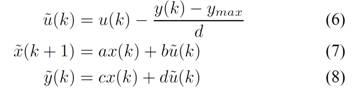
При текущем периоде дискретности этот алгоритм корректирует переменную состояния от x(k + 1) до ^x(k + 1). Как результат, регулятор не имеет явления насыщения, вызванного собственным ограничением выходного сигнала. Когда y меньше y_max, компенсация насыщения алгоритм не выполняется.

Рисунок 8 – Блок-схема предлагаемой системы позиционирования<>

На рис. 9 показана форма идеального высокоскоростного позиционирования в случае малого перемещения. В этом случае ошибка положения достигает Δθ_m^err до достижения двигателем скорости, равной ω_max. Даже в этом случае предложенный алгоритм позволяет завершить высокоскоростное позиционирование, используя (3).

Рисунок 9 – Идеальная осциллограмма высокоскоростной системы позиционирования (малое перемещение)

4. Результаты численного моделирования

Численное моделирование проводится для подтверждения эффективности предлагаемого алгоритма высокоскоростного позиционирования. Условия численного моделирования заключаются в следующем:

1) без момента сопротивления, θ_m^ref = 6π [рад]

2) с половинным моментом сопротивления, θ_m^ref = 6π [рад]

3) с половинным моментом сопротивления, θ_m^ref = π [рад]

Модель создания трения в испытуемой экспериментальной системе, показанная на рис. 6, показана на рис. 10 и в таблице III.

В этой статье рассматривается обычный наблюдатель возмущений, показанный на рис.11. Наблюдатель возмущений, частота которого составляет 400 [рад/с] и период дискретности 100 [μсек]. На рис.11 коэффициент усиления g и T_s определяется как (9) и (10).

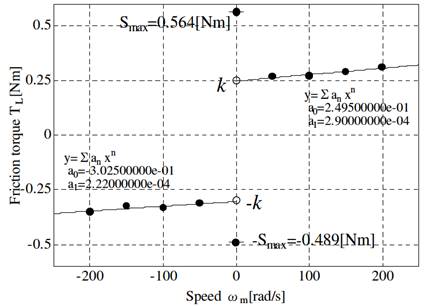
Рисунок 10 – Идентификация модели трения

Таблица III

Модель трения в численном моделировании

Положительный	максимальный статический		Smax[Nm]	0.564
	кинетический	вязкий	D[Nm/rad/s]	2.9x10-4
		сухой	K[Nm]	2.495x10-1
Отрицательный	максимальный статический		- Smax[Nm]	0.489
	кинетический	вязкий	- D[Nm/rad/s]	2.22x10-4
		сухой	- K[Nm]	3.025x10-1

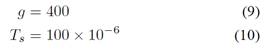
Результаты каждого численного моделирования показаны на рис. 12, рис. 13 и рис. 14. На рис. 12 сервомотор ускоряется и замедляется с использованием максимального крутящего момента + i_max без момента сопротивления. На рис.13 подтверждается, что серводвигатель аналогичным образом ускоряется с использованием максимального крутящего момента + i_max с половинным номинальным моментом сопротивления. Наконец, скорость двигателя замедляется в момент времени t₂ на основании расчетного момента сопротивления сухого трения T_L, на этом позиционирование завершено. На рис. 14 сервомотор ускоряется с использованием максимального тока + i_max, а режим замедления запускается до достижения двигателем скорости ω_max. Полученные результаты численного моделирования являются почти идеальными.

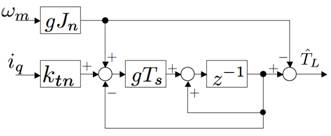
Рисунок 11 – Структурная схема наблюдателя возмущений

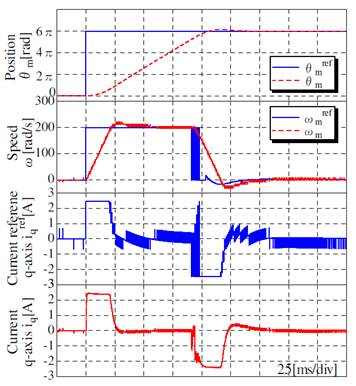
Рисунок 12 – Результаты численного моделирования (без момента сопротивления)

Рисунок 13 – Результаты численного моделирования (с половинным моментом сопротивления)

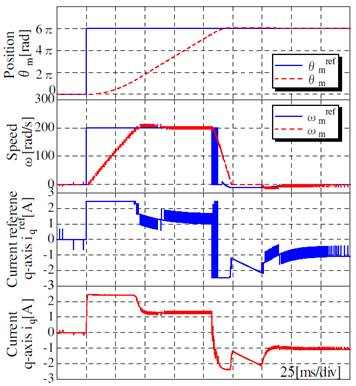
Рисунок 14 – Результаты численного моделирования (с половинным моментом сопротивления и θ_m^ref = π[рад])

5. Результаты эксперимента

Экспериментальные результаты без момента сопротивления представлены на рис. 15, а на рис. 16 представлены результаты эксперимента с половинным моментом сопротивления с помощью системы торможения. Оба экспериментальных результата являются хорошими, поскольку режим ускорения и торможения используют максимальный крутящий момент серводвигателя при условии большого момента сопротивления. С точки зрения рис. 4 и рис. 5 предлагаемая система позиционирования имеет более высокую производительность, чем обычная система позиционирования. Когда задание на положение мало, как показано на рис. 17, предлагаемая система позиционирования также имеет высокую скорость позиционирования. Данные экспериментальные результаты также являются желательными, которые также почти равны идеальным результатам.

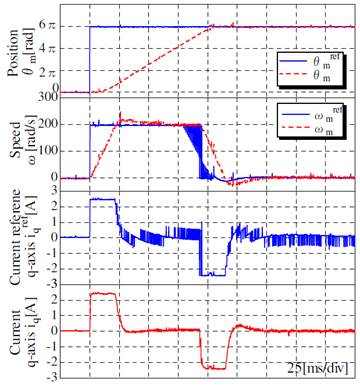
Рисунок 15 – Экспериментальные результаты с предлагаемой системой (без момента сопротивления)

Рисунок 16 – Экспериментальные результаты с предлагаемой системой (с половинным моментом сопротивления)

Рисунок 17 – Экспериментальные результаты с предлагаемой системой (θ_m^ref = π[рад])

6. Вывод

В данной статье предлагается новая высокоскоростная система позиционирования серводвигателя переменного тока с учетом неизвестного сухого трения и явления насыщения. В предлагаемой системе всегда используется максимальный момент при разгоне или торможении, а так же максимальная скорость. В предлагаемом алгоритме используется нагрузка в виде сухого трения. В данной статье крутящий момент сухого трения оценивается наблюдателем возмущений.

Чтобы подтвердить правильность предлагаемого алгоритма высокоскоростного позиционирования, в этой статье представлены результаты численного моделирования и экспериментальные результаты реакции системы на скачёк. Условия эксперимента и численного моделирования следующие:

1) задание на положение θ_m^ref = 6π [рад], без нагрузки

2) задание на положение θ_m^ref = 6π [рад], с половинной нагрузкой

3) задание на положение θ_m^ref = π [рад], с половинной нагрузкой

Экспериментальные результаты и результаты численного моделирования указывают на то, что предлагаемая высокоскоростная система позиционирования всегда имеет желаемую реакцию по положению, которая почти равна идеальной реакции.

Ссылки

[1] K.Sakai, M.Iwasaki and N.Matsui High-Speed and High-Precision Positioning System by Using Mode Switching Control,T.IEE Japan,Vol.118-D, No.7/8,pp.870-876(1998-7/8)(in Japanese)

[2] T.Mashimo, K.Ohishi and H.Dohmeki High speed positioning system considering load torque for servo motor, The Papers of Technical Meeting on Industrial Instrumentation and Control, IEE Japan, IIC-03-27, pp.69-74 (2003) (in Japanese)

[3] M.Nakao, M.Kim, K.Ohishi and K.Ohinish Suppression of Wind-up Phenomena in Digital Servo Drive System,T.IEE Japan,Vol.108-D, No.7,pp.678-684(1988-7)(in Japanese)

[4] R.Hanus, M.Kinnaert and J.L.Henrotte,Conditioning Technique, a General Anti-windup and Bumpless Transfer Method, Automatica,Vol.23,No.6,pp.729-739,1987

[5] F.Suzuki and Y.Hori Anti-Windup Control using Saturated State Observer, T.IEE Japan,Vol.120-D, No.1,pp.120-125(2000-1)(in Japanese)

[6] K.Ohishi and T.Mashimo, Digital Robust Speed Servo System with Complete Avoidance of Output Saturation Effect, Proc. of International Joint Conference of IEE. of Japan IAS. and IEEE. IAS. PCCNAGAOKA’ 97, pp.501-506, 1997

[7] K.Ohishi and T.Mashimo Design Method of Digital Robust SPeed Servo System Considering Output Saturation,T.IEE Japan,Vol.119-D, No.1,pp.88-96(1999-1)(in Japanese)