Аннотация
Ворачева А.И. Исследование трехфазного короткого замыкания в простейшей цепи. Рассмотрены системы блочного моделирования. Рассмотрены электромагнитные переходные процессы в цепях с сосредоточенными параметрами.
Курс Переходные процессы в электрических системах
является одним из профилирующих для электроэнергетических специальностей, и его положения используются как при проектировании, так и при управлении функционированием электроэнергетических систем и систем электроснабжения предприятий [10]
Переходные процессы возникают в электрических системах как при нормальной эксплуатации (включение и отключение нагрузок, источников питания, отдельных цепей, производство испытаний и т.д.), так и в аварийных условиях (обрыв провода, короткое замыкание, выпадение машины из синхронизма и т.д.). Их изучение необходимо прежде всего для ясного представления причин возникновения и физической сущности этих процессов, а так же для разработки методов их количественной оценки, для того чтобы можно было предвидеть и заранее предотвратить опасные последствия таких процессов.
Переходный процесс характеризуется совокупностью электромагнитных и механических изменений в системе. Но при относительно малых возмущениях (короткое замыкание за большим сопротивле-нием) весь переходный процесс можно рассматривать только как электромагнитный [3]
Рассмотрение электромагнитных переходных процессов в цепях с сосредоточенными параметрами реализовано в виде разработки методических указаний для выполнения лабораторной работы по курсу Электромагнитные переходные процессы в электрических системах
. Данная работа ставит целью более детально рассмотреть ряд узловых положений курса путем проведения экспериментальных исследований на ПЭВМ и осмысления результатов, приобретения навыков инженерного мышления [2]
Целью данной лабораторной работы является исследование влияния режима, предшествующего короткому замыканию, и момента возникновения короткого замыкания на токи в элементах сети.
В данной работе используется простейшая трехфазная цепь с сосредоточенными активными и индуктивными сопротивлениями, питание которой осуществляется от источника бесконечной мощности.
На рис.1 представлена простейшая симметричная трехфазная цепь. В ней условно принято, что на линейном участке имеется взаимоиндукция между фазами (М). Цепь присоединена к источнику синусоидального напряжения с неизменными амплитудой и частотой. Тип нейтрали – изолированная[1]
Для отечественных пользователей удобство работы с ПК МВТУ
обусловлено русскоязычным интерфейсом и наличием обширной документации на русском языке. Учебная и демонстрационная версии ПК МВТУ
вместе с полной документацией и набором демонстрационных примеров распространяются свободно[1]. В учебной версии есть ограничения на сложность модели: порядок дифференциальных уравнений не выше 30, а число блоков не более 100. В демонстрационной версии таких ограничений нет, но модель нельзя сохранить.
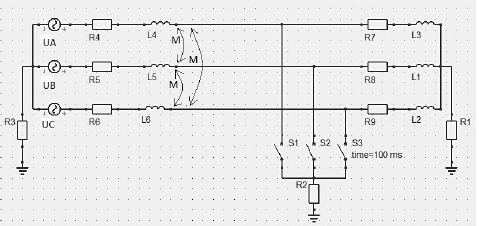
Рисунок 1 – Принципиальная схема простейшей трехфазной цепи
После замыкания трехфазного ключа S (S1, S2 и S3) цепь распадается на два независимых друг от друга участка. Участок с нагрузкой оказывается зашунтированным закороткой в месте КЗ, и токи в каждой фазе будут поддерживаться за счет запасенной в индуктивностях энергии и затем выделятся в виде тепла на активном сопротивлении.
Интерес представляет участок цепи, который остался присоединенным к источнику. Дифференциальное уравнение равновесия мгновенных токов и напряжений для любой фазы, например фазы А, этого участка

Где L – собственная индуктивность фазного провода, M – взаимоиндуктивность между отдельными проводами. Имея в виду, что

Решение уравнения (2) имеет вид:
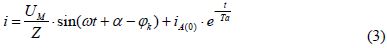
Где Z – полное сопротивление присоединенного к участку источника цепи, φk – угол сдвига тока в этой цепи, Ta – постоянная времени цепи короткого замыкания [1].
Здесь помимо свободного тока будет присутствовать принужденный ток, величина которого больше тока предыдущего режима и сдвиг по фазе в общем случае иной.
Анализируя решение (3) обнаруживаются две составляющие: периодическая слагающая тока КЗ iп и апериодическая ia.
Первая составляющая – принужденный ток с постоянной амплитудой IПM. Соответственно вторая составляющая представляет затухающий по экспоненте ток – апериодическая слагающая тока. Графически это представлено на рис.2.

Рисунок 2 – Осциллограмма тока переходного процесса
Наибольшее значение апериодической составляющей определяется не только фазой включения, но так же предшествующим режимом цепи.
В практических расчётах максимальное мгновенное значение полного тока короткого замыкания, которое называют ударным током короткого замыкания iy, обычно находят при наибольшем значении апериодической слагающей, считая, что он наступает приблизительно через полпериода с момента возникновения короткого замыкания.
Таким образом, выражение для ударного тока короткого замыкания можно записать в следующем виде:

Где

Который называют ударным коэффициентом, показывает превышение ударного тока над амплитудой периодической слагающей, его величина находится в пределах 1–2 [1].
Естественно, что апериодические слагающие токов в фазах различны, поэтому определение трехфазного короткого замыкания как симметричного, справедливо применительно к периодическим слагающим фазных токов.
В данной работе предлагается смоделировать простейшую трехфазную цепь в программной среде Qucs. Qucs, также известный как Quite Universal Circuit Simulator, был разработан как доступный симулятор электронных цепей и контуров, имеющий графический интерфейс. Программа поддерживает все виды моделирования схем: на постоянном, переменном токе, моделирование переходных процессов и многое другое. Результаты моделирования можно посмотреть на странице презентации или окне программы, что очень удобно при анализе результатов, т.к. изменение контролируемых параметров представлено в виде графиков.
В качестве задания предлагается для двух конфигураций цепей: с нагрузкой и без, по уравнениям тока короткого замыкания, приведенным выше, рассчитать значение принужденного, свободного тока КЗ в фазе и ударный коэффициент. Затем произвести моделирование в предлагаемой программной среде и сравнить результаты моделирования с расчетными значениями. Так же необходимо выявить режим, при котором апериодическая составляющая тока КЗ наибольшая и обосновать результат.
Литература
1. Ульянов С.А. Электромагнитные переходные процессы в электрических системах. М.:Энергия, 1964. ?518 с.,1970. ?518 с.
2. Готман В.И Электромагнитные переходные процессы в электрических системах. Методические указания к выполнению лабораторных работ. – Томск.: Издательство ТПУ, 2003. – 40 с., ил.
3. Борисов Р.И., Готман В.И. Основы переходных процессов в электрических системах. Томск:Изд. ТПИ, 1969. ?388 с.