Реферат за темою випускної роботи
Зміст
- Введение
- 1. Постановка задачі
- 2. Мета, аналіз досліджень і публікації
- 3. Результати досліджень
- 4. Приклад
- Висновки
- Перелік посилань
Вступ
Використовуючи поняття переріз
, мінімальний переріз
, запропонований метод оцінки надійності складних по структурі систем, елементи яких можуть знаходиться в трьох несумісних станах: працездатне, не працездатне (відмова типу обрив ланцюга
і відмова типу коротке замикання
).
Наведено приклад розрахунку.
Ключові слова: система, мінімальний переріз, складна схема, ймовірність, вузол навантаження.
1. Постановка задачі
Для оцінки надійності складних невідновлювальних систем, елементи яких можуть знаходиться в трьох несумісних станах, використовують метод мінімальних перерізів
. [1–2].
Слід розібрати новий принцип побудови схем заміщення для оцінки надійності складних невідновлювальних систем таким чином,
щоб цей метод дозволив оцінювати надійність систем, елементи яких можуть знаходиться в трьох несумісних станах (працездатний,
непрацездатний – відмова типу обрив ланцюга
, непрацездатний – відмова типу коротке замикання
), що дозволить враховувати в схемах заміщення систем електропостачання відмови в спрацьовуванні захисних комутаційних апаратів, і, таким чином, значно підвищити точність розрахунків.
2. Мета, аналіз досліджень і публікації
Мета роботи: вдосконалення методу оцінки надійності складних невідновлювальних систем, елементи яких можуть знаходиться в двох несумісних станах.
Для оцінки надійності складних невідновлювальних систем, елементи яких можуть знаходиться в трьох несумісних станах,
відомі три методи, засновані на використанні: розкладання складної структури по базовому елементу, застосування перетворень трикутник-зірка
и зірка-трикутник
, а також на використанні алгебри кортежів. [3–6]
Усі пропоновані методи досить складні у використанні для інженерних розрахунків, тому вдосконалення методу мінімальний переріз
дозволить досить просто отримати нижню оцінку ймовірності безвідмовної роботи системи при обліку двох видів несумісних відмов її елементів.
3. Результати досліджень
До невідновлюваних будемо відносити такі системи, відновлення яких з яких-небудь причин неможливо в розглянутий період часу [1].
Елементи з трьома несумісними станами: працездатне, відмова типу обрив ланцюга
і відмова типу коротке замикання
можна виділити в системах таких як водопровід, що подає повітря трубопроводи, газопроводи, продуктопроводи і т.д.
Аналогами елементів з трьома станами в таких системах можуть бути крани, вентилі, різних типів, запірна арматура, заглушки, і ін. Види переривників потоку (рідини, газу і т.д.), для яких в непрацездатному стані потік не переривається (коротке замикання
) або не передається (обрив ланцюга
) [3].
Захисних комутаційний апарат і електрообладнання, яке входить в зону дії його автоматичних засобів захисту будемо розглядати як елемент системи, який може знаходитися в трьох несумісних станах.
До відмов типу ( коротке замикання
, будемо відносити такі пошкодження: (КЗ) в захищуваному елементі мережі, при якому відбувається відмова в спрацьовуванні автоматичної системи відключення комутаційного апарату, тобто коли через даний комутаційний апарат проходить наскрізний струм, а система його основний (РЗ) не спрацьовує.
Для оцінки надійності технічних систем широкого поширення набули елементні методи [7–10].
У цих методах пропонується, що електрообладнання в схемах заміщення систем електропостачання складається з самостійних (в сенсі аналізу надійності) елементів.
Під вузлами
схеми заміщення розуміються фізичні пункти, які безпосередньо пов'язані не менше ніж з трьома напрямками передачі енергії, тобто це зазвичай збірні шини або секції розподільчих пунктів [9].
Використовуючи принципову схему системи електропостачання, складається схема заміщення для оцінки надійності споживачів, які отримують електроенергію від розглянутого вузла навантаження.
Всі незалежні джерела електропостачання системи об'єднуються в одну точку, і вона вважається абсолютно
надійної і є входом
схеми заміщення [8–10].
Все повреждения в схеме электроснабжения выше выбранной точки входа
в расчетах не учитываются.
Выходом
схемы замещения системы электроснабжения является сборные шины, от которых получают электроэнергию потребители.
Припустимо, що всі розглянуті елементи, з яких складається система, можуть відмовляти незалежно один від одного;
Кожен елемент системи може знаходиться в трьох несумісних станах: працездатному, непрацездатному - відмова типу обрив ланцюга
,
непрацездатному - відмова типу коротке замикання
; потоки відмов елементів (типу обрив ланцюга
) і (типу коротке замикання
) найпростіше;
пропускна здатність елементів необмежена так само, як і здатність стримувати потік енергії (рідини, газу, електричного струму) незалежно від кількості короткозамкнутих елементів;
після виходу з ладу елемент не відновлюється (не замінювати на новий) у розглянутий період часу [3].
Позначимо через Pi ймовірність безвідмовної роботи i
-того елемента системи,
qOi – ймовірність появи відмов в i
-том елементі типу обрив ланцюга
,
а через qSi – ймовірність появи відмов в i
-том елементі типу коротке замикання
. Ці три стани складають повну групу несумісних подій.
 |
(3.1) |
Індекс O
и S
у формулі вказують на те, що враховуються пошкодження елемента, які призводять до відмов типу обрив ланцюга
, або відмов типу коротке замикання
, відповідно.
У тому випадку, якщо елементи системи схильні до двох типів несумісних відмов: відмова типу обрив ланцюга
і відмова типу коротке замикання
, тоді ймовірність його відмов протягом часу t можна визначити наступним чином [4]:
 |
(3.2) |
где λOi,λSi – постійні інтенсивності відмов i
-того елемента при врахуванні його відмов типу обрив ланцюга
і типу коротке замикання
, відповідно;
t – текущее время работы i
-того элемента системы.
Під ймовірністю безвідмовної роботи невідновлювальної системою, елементи якої можуть знаходиться в трьох несумісних станах, будемо вживати заходів її надійності,
яка характеризується ймовірністю того, що в перебігу заданого інтервалу часу не пройдуть такі випадкові події,
в результаті яких розривається зв'язок або проходить наскрізний аварійний струм між входом
и виходом
схеми заміщення, за умови, що в початковий момент часу всі її елементи перебуває в працездатному стані.
Для невідновлювальних систем, елементи яких можуть знаходиться в трьох несумісних станах, справедлива формула:
 |
(3.3) |
где RH – нижня оцінка ймовірності того, що не буде такі випадкові події, в результаті яких розірветься зв'язок або пройде наскрізний аварійний струм між вузлами Вхід
и Вихід
схеми заміщення;
QOH,QSH – нижня оцінка ймовірності того, що відбудеться розрив зв'язку або пройде наскрізний аварійний струм між вузлами Вхід
и Вихід
схеми заміщення, відповідно.
Під простий за визначенням схемою заміщення системи будемо розуміти таку, елементи якої можуть з'єднатися: послідовно, паралельно, послідовно-паралельно, або паралельно-послідовно.
Для простої щодо визначення схеми заміщення системи, яка складається з n
логічно послідовного з'єднання елементів, відмова типу обрив ланцюга
будь-якого з n
елементів (i = 1...n), призводить до розриву зв'язку між вузлами Вхід
и Вихід
.
Якщо задані ймовірності відмов елементів схеми заміщеннято qOi, то ймовірність розриву зв'язку між вузлами Вхід
и Вихід
QO визначимо наступним чином:
 |
(3.4) |
У тому випадку, якщо у кожного з n
логічно послідовного з'єднання елементів відбудеться відмова типу коротке замикання
в кожному з i
елементів, то це призведе до того, що між вузлами Вхід
и Вихід
схеми заміщення пройде наскрізний аварійний струм.
Якщо задані ймовірності відмов елементів схеми заміщення qSi, то ймовірність QO того, що між вузлами Вхід
и Вихід
схеми заміщення пройде наскрізний аварійний струм, знайдемо за допомогою формули:
 |
(3.5) |
Використовуючи формули (3-5), знаходимо для системи, яка складається з n
логічно послідовного з'єднання елементів ймовірність Rn того, що не пройдуть такі випадкові події, в результаті чого розірветься зв'язок або пройде наскрізний аварійний струм між вузлами Вхід
и Вихід
схеми заміщення:
 |
(3.6) |
Для простой
заміщення системи, яка складається з m
логічно паралельно з'єднаних елементів, відмова типу обрив ланцюга
в кожному з j
елементів (j = 1...m), призводить до обриву зв'язку між вузлами Вхід
и Вихід
.
Якщо задані ймовірності відмов елементів схеми заміщення qOi, то ймовірність QO того, що станеться розрив зв'язку між вузлами Вхід
и Вихід
знаходимо, користуючись формулою:
 |
(3.7) |
У тому випадку, якщо у будь-якого з m
логічно паралельно з'єднаних елементів відбудеться відмова типу коротке замикання
, то це призведе до того, що між вузлами Вхід
и Вихід
схеми заміщення пройде наскрізний аварійний струм.
Якщо задані ймовірності відмов qSj, (j = 1...m) елементів схеми заміщення, яка складається з m
логічно паралельно з'єднаних елементів, тоді QS – ймовірність того, що між вузлами Вхід
и Вихід
схеми заміщення пройде наскрізний аварійний струм, знайдемо, використовуючи формулу:
 |
(3.8) |
Підставивши формули (7-8) в формулу (3) знаходимо, що для системи, яка складається з m
логічно паралельно з'єднаних елементів, ймовірність Rm того, що не пройдуть такі випадкові події, в результаті чого рветься зв'язок або проходить наскрізний аварійний струм між вузлами Вхід
и Вихід
схеми заміщення:
 |
(3.9) |
Формули (7) и (10) справедливі при виконанні умови: qOi + qSi < 1, qOj + qSj < 1 і отримані різними способами [4–5].
Під складною
схемою заміщення системи будемо розуміти таку, до складу якої входить хоча б одна група елементів, з'єднаних у вигляді бруківці
стуктури [11].
Для приведення складної
схеми заміщення, елементи якої піддаються відмов типу обрив ланцюга
, до простої
, скористаємося поняттям переріз
и мінімальний переріз
[[1].
Під мінімальним перерізом
C
схеми заміщення складної
системи будемо розуміти переріз
, у якого припускаємо, що хоча б один елемент виявився абсолютно надійним, в результаті чого відмови типу обрив ланцюга
залишилися в цьому перерізі
елементів не буде більше складати переріз
, так як при цьому не відбувається розрив зв'язку між входом
и виходом
.
Використовуючи вихідну схему заміщення складної
структури, поняття мінімальний переріз
Cmin, враховуючи, що елементи системи піддаються відмов типу обрив ланцюга
і якщо задані ймовірності відмов кожного з i
елементів qOi,(i = 1...n), будуються схеми мінімальних перерізів
.
Під мінімальним перерізом
Cmin
складної схеми заміщення системи будемо розуміти перетин, у якого припускаємо, що хоча б один елемент виявився абсолютно надійним, в результаті чого відмови типу коротке замикання
залишилися в цьому перерізі
елементів вже не буде більш складати переріз
, так як при цьому не відбувається протікання наскрізного аварійного струму між вузлами Вхід
и Вихід
.
Використовуючи вихідну схему заміщення складної
системи, поняття Cmin
, враховуючи, що в елементах системи спостерігаються відмови типу коротке замикання
і відомі ймовірності відмов кожного з її i
елементів qSi,(i = 1...n), будуємо схему мінімальних перерізів
.
4. Приклад

Рисунок 1 – Схема заміщення системи
Для схеми заміщення системи рис 1 задані наступні вихідні дані:
 |
Визначити нижню оцінку RH
того, що не відбудеться розрив зв'язку або не пройде наскрізний аварійний струм між точкою входу
и виходу
схеми заміщення.
Використовуючи поняття мінімальний переріз
, схему рис 1, схема мінімальних перерізів
при обліку відмов типу обрив ланцюга
набуде вигляду:
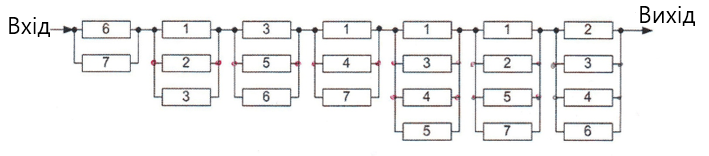
Рисунок 2 – Схема мінімальних перерізів
при обліку відмов елементів типу обрив ланцюга
Використовуючи схему заміщення рис. 2, формули (4), (7) знаходимо:
 |
Підставляємо в отриману формулу значення: qOi (i = 1...7), задані в умові прикладу, отримаємо:
 |
Використовуючи поняття мінімальний переріз
, схему рис 1, схема мінімальних перерізів
при обліку відмов типу коротке замикання
набуде вигляду:
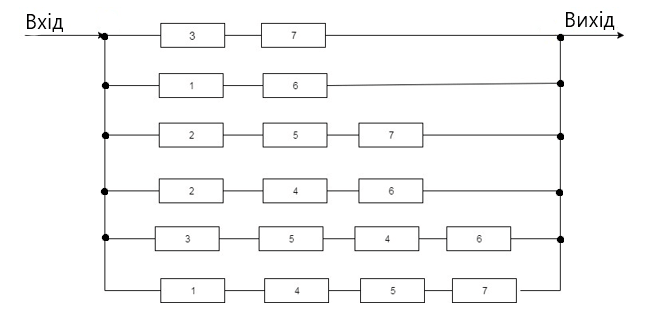
Рисунок 3 – Схема мінімальних перерізів
при обліку відмов елементів типу коротке замикання
Використовуючи отриману схему заміщення рис. 3, формули (5), (8), знайдемо нижню оцінку QSH ймовірності того, що відбудеться подія, при якому наскрізний аварійний струм пройде між вузлом
Вхід
и Вихід
схеми заміщення:
 |
Використовуючи вихідні дані прикладу, підставляємо їх в отриману формулу:
 |
Імовірність того, що не відбудеться розрив зв'язку або не пройде наскрізний аварійний струм між вузлом
Вхід
и Вихід
схеми заміщення знайдемо, використовуючи формулу (3):
 |
Підставимо отримані значення QOH и QSH в формулу і визначимо:
 |
Аналогічний результат був отриманий при вирішенні цього завдання, використовуючи точний метод розрахунків з використанням способу розкладання складної структури за базисним елементу [3].
5. Висновки
1. Запропоновано інженерну методику розрахунків надійності складних невідновлювальних систем, елементи яких можуть знаходиться в трьох несумісних станах.
2. Точність пропонованої методики для високонадійних систем (вероятностьотказов елементів схеми заміщення менше, або дорівнює 0,1) не поступається точним, апробованими методами.
Перелік посилань
- Надежность технических систем: Справочник Ю.К. Беляев, В.А. Богатырев, В.В.Болотин и д.р.; Под ред. И.А. Ушаков. – М.: Радио и связь, 1985. – 608с.
- Рябинин И.А. Надежность и безопасность структурно сложных систем. СПБ.:Изд-во С. – Петербург ун-та, 2007. – 276с.
- Ковалев А.П., Спиваковский А.В. Применение логико-вероятностных методов для оценки надежности структурно-сложных систем. Электричество №9, 2000. – с.66-70.
- Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности систем: Пер.с англ. – М.: Мир, 1984. – 318с.
- Ковалев А.П., Спиваковский А.В. О преобразовании «Звезда-треугольник» прирасчетах надежности сложных по структуре схем. Электричество №10, 1998 – с.70-74.
- Кулик Б.А. Логико-вероятностные методы и алгебра кортежей. – В сб.: Теория иинформационная техника моделирования безопасности сложных систем, – Санкт-Петербург: ИПМАШРАН, Препринг 123, вып. 1995, вып 5.
- Нечипоренко В.И. Структурный анализ систем (эффективность и надежность) – М.: Советское радио, 1977. – 214с.
- Эндрени Дж. Моделирование при расчетах надежности в электроэнергетическихсистемах: Пер. с англ. /Под ред. Ю.Н. Руденко М.: Энергоатомиздат, 1983 – 336с.
- Фонин Ю.А., Харченко А.М. Расчет надежности систем электроснабжения. – Электричество, 1982, №8 с.5-10.
- Белоусенко И.В., Ершов А.М., Ковалев А.П., Якимишена В.В, Шевченко О.А. О расчете надежности систем электроснабжения газовых промыслов. Электричество, 2004, №3. с.22-27.
- Ковалев А.П., Сердюк Л.И. Метод расчета надежности сложных схем систем электроснабжения с учетом восстановления элементов. – Электричество, 1985, №10 с. 52-53.
