Оценка надежности сложных по структуре невосстанавливаемых систем
Источник: Инновационные перспективы Донбасса, г. Донецк, 24-26 мая 2017 г. – Донецк: ДонНТУ, 2017 / Т.2: Перспективы развития электротехнических, электромеханических и энергосберегающих систем. – 2017, Секция 2, с. 266-271.
Авторы: Дьяченко Д.Ю., Воронин Д.И., Ковалев А.П.
Аннотация
В данной работе предложен метод расчетов надежности структурно-сложных схем, невосстанавливаемых систем, который основан на использовании теоремы о сумме вероятностей несовместных событий и отличается от известных тем, что не использует в расчетах функции алгебры логики, это значительно упрощает расчеты и моделирование на ПК.
Основные понятия, допущения и определения
К невосстанавливаемым в процессе эксплуатации системам будем относить такие системы, восстановление которых по каким-либо причинам невозможно непосредственно в рассматриваемый период времени [1].
Пусть система состоит из конечного числа элементов. Предположим, что отказы элементов системы статистически независимы. Потоки отказов элементов системы стационарны, ординарны и не имеют последствия. Учитываются повреждения элементов типа обрыв цепи
. При выходе из строя любого из элементов системы, восстановление или замена его не возможна в рассматриваемый интервал времени. Считаем, что автоматические средства релейной защиты в коммутационных аппаратах абсолютно надежны.
Пусть каждый элемент схемы замещения характеризуется вероятностью безотказной работы Pi, i = 1...n. В схеме замещения выделяется вход и выход системы.
Все источники электроснабжения системы объединяются в одну точку, и эта точка считается абсолютно надежной.
В качестве выхода системы используются узлы нагрузки
, откоторых электроэнергия предается потребителям (система сборных шин).
Под простой
по структуре схемой замещения будем понимать такую, элементы которой могут соединяться: последовательно, параллельно, последовательно-параллельно, параллельно-последовательно.
Для приведения «простых» по структуре схем к одному эквивалентному по надежности элементу используются следующие формулы [2].
Вероятность безотказной работы Rn схемы замещения, которая состоит из n
логически последовательного соединения элементов находится с помощью формулы:
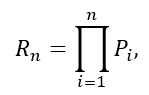 |
(1) |
где Pi – вероятность безотказной работы i-го элемента схемы замещения (i = 1...n.)
Вероятность безотказной работы Rm схемы, которая состоит из m
логически параллельного соединения элементов запишем в виде:
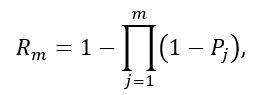 |
(2) |
где Pj – вероятность безотказной работы j-го элемента схемы замещения (j = 1...m.)
Под сложной
по структуре схемой замещения системы электроснабжения будем понимать такую схему, в состав которой входит хотя бы одна мостиковая
структура [3].
Способ преобразования сложной по структуре схемы замещения по базовому элементу
Способ преобразования сложной по структуре схемы замещения, основан на использовании теории о сумме вероятностей несовместных событий [4].
Примечательно к задачам оценки надежности систем электроснабжения эта теорема может быть использована следующим образом.
Предположим, что элемент сложной структуры может находиться в двух несовместных состояниях: работоспособное и не работоспособное (отказ типа обрыв цепи
).
В сложной по структуре схеме замещения выбираем базовый элемент.
Чаще всего в качестве базового элемента следует выбрать такой элемент, который соединяет между собой два узла
схемы замещения.
Под узлом
будем понимать точку в схеме замещения, которая соединяет между собой три и более линии.
В том случае, если базовый элемент выбран, например, это элемент в схеме замещения стоит под номером i
, тогда выдвигаем гипотезу и делаем два допущения:
– базовый элемент i
абсолютно надежен и способен пропускать через себя нагрузку потребителям электрической энергии;
– базовый элемент i
абсолютно не надежен и не пропускает через себя нагрузку потребителям электрической энергии.
Для этих случаев, представляющих собой два несовместных события, исходная сложная схема замещения (рисунок 1а) преобразуется в две новые (рисунок 1б) и (рисунок 1в).
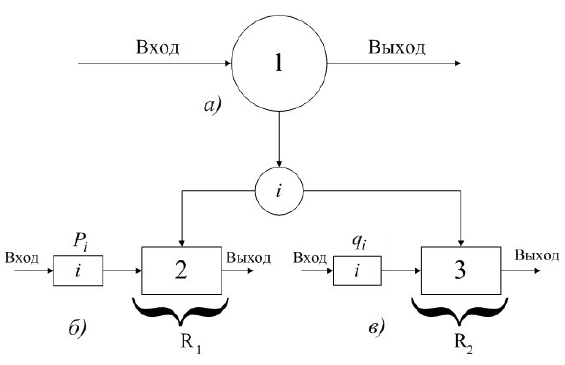
Рисунок 1 – Способ преобразования сложной
по структуре схемы замещения по базовому элементу i
;
1 – схема замещения исходной сложной
структуры;
2,3 – схемы замещения полученных простых
структур.
В схеме (рисунок 1б) вместо базового элемента i
ставится абсолютно надежная линия с неограниченной пропускной способностью.
Последовательно с полученной схемой подсоединяется базовый элемент i
. Вероятность безотказной работы базового элемента равна Pi.
В схеме замещения (рисунок 1в) в том месте, где находился элемент i
разрывается цепь. Последовательно с полученной схемой подсоединяется базовый элемент i
, вероятность отказов которого равна qi = 1 - Pi.
Полученные после преобразования сложной по структуре схемы (рисунок 1а) по базовому элементу i
две новые схемы (рисунок 1б) и (рисунок 1в), анализируются. Если окажется, что обе полученные схемы будут простыми
, тогда используются формулы (1) и (2) вычисляются их вероятности безотказной работы R1 и R2 соответственно. Вероятности безотказной работы R1 и R2 умножаются первая на Pi, а вторая на qi.
Используя теорему о сумме вероятностей несовместных событий, вероятность безотказной работы R сложной схемы замещения (рисунок 1а) находим следующим образом:
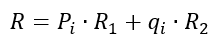 |
(3) |
В том случае, если, например, после преобразования сложной схемы замещения (рисунок 2а) по базовому элементу i
в результате получилось, что одна из схем преобразования (рисунок 2б) будет простой
, а (рисунок 2в) сложной
, тогда в схеме (рисунок 2в) выбираем базовый элемент j
и она раскладывается на две новые (рисунок 2г) и (рисунок 2д).
В схеме (рисунок 2г) вместо базового элемента j
ставится абсолютно надежная линия с неограниченной пропускной способностью. Последовательно с базовым элементом i
подсоединяется базовый элемент j
, вероятность безотказной работы, которого равна Pj
В схеме замещения (рисунок 2д) в том месте, где находился элемент j
разрывается цепь.
Последовательно с базовым элементом i
подсоединяется базовый элемент j
с характеристикой надежности qj = 1 - Pj
После преобразования схемы замещения (рисунок 2в) по базовому элементу j
, получим две новые: (рисунок 2г) и (рисунок 2д), после этого они анализируются. В том случае, если обе полученные схемы простые
, тогда используя формулы (1) и (2) находим их вероятности безотказной работы R2 и R3 соответственно.
Полученные вероятности безотказной работы умножаются на соответствующие вероятности базовых элементов i
и j
т. е. PjqiR2, qjqiR3.
Используя теорему о сумме вероятностей несовместных событий, вероятность безотказной работы схемы (рисунок 2в) определяется с помощью формулы:
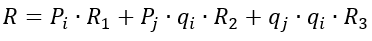 |
(4) |
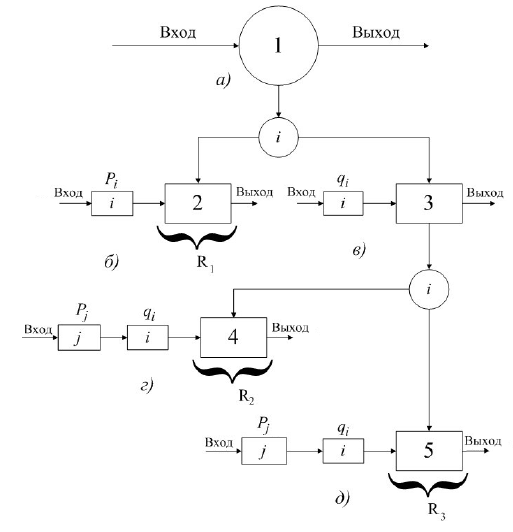
Рисунок 2 – Способ преобразования сложной
по структуре схемы замещения по базовому элементу i
и j
;
1 – Исходная схема замещения сложной структуры;
2,4,5 – Схемы замещения полученных простых
структур;
3 – Схема замещения сложной
структуры.
В том случае, если после преобразования схемы (рисунок 2в) по базовому элементу i
получилось, что схема (рисунок 2д) оказалась сложной
, тогда процедура преобразования по вновь выбранному базовому элементу будет продолжаться до тех пор, пока все схемы после их преобразования не будут простыми
.
Вероятность безотказной работы исходной схемы в этом случае будет определяться суммой вероятностей безотказной работы полученных простых
схем, с учетом соответствующих каждой схеме последовательно соединенных базовых элементов.
Выводы
Предлагаемый метод оценки надежности структурных сложных систем, без учета восстановления элементов, отличается от известного [1] тем, что вместо использования уравнений и понятий алгебры логики применяются привычные в инженерной практике схемы замещения реальной системы, это в значительной мере упрощает расчеты и моделирование на ПК.
Список использованной литературы
1. Козлов Б.А., Ушаков И.С. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики. – М.: Сов. радио. 1975. – 472с.
2. Б. Диллон., Ч. Сингх. Инженерные методы обеспечения надежности систем. Пер. с англ. – М.: Мир, 1984 – 318с.
3. Ковалев А.П., Сердюк Л.И. Метод расчета надежности сложных систем электроснабжения с учетом восстановления элементов. – Электричество, 1985, №10. с. 52-53
4. Вентцель Е.С. Теория вероятностей. – М.: Наука. 1964 – 576с.
5. Рябинин И.А. Основы теории и расчета надежности судовых электроэнергетических систем 2е-изд. – Л.: Судостроение, 1971. – 456с.