Адаптивная антенная решетка в арифметике действительных чисел

Аннотация

В работе рассмотрен способ организации комплексных вычислений в арифметике действительных чисел применительно к адаптивным антенным решеткам с линейными ограничениями на базе рекурсивного алгоритма по критерию наименьших квадратов, принимающих сигналы, характеризующиеся постоянным значением комплексной огибающей. Результирующий алгоритм адаптивной фильтрации имеет примерно в 2 раза меньшую вычислительную сложность по сравнению с исходным алгоритмом в арифметике комплексных чисел, в 1.5-2 раза меньшую длительность переходного процесса и в среднем обеспечивает на 2-4 дБ более глубокие провалы в диаграмме направленности антенной решетки в направлениях источников помех в установившемся состоянии. Приведена вычислительная процедура алгоритма адаптивной фильтрации, а также результат моделирования, подтверждающий работоспособность и эффективность этого алгоритма по сравнению с аналогичным алгоритмом в арифметике комплексных чисел.

Ключевые слова

адаптивная антенная решетка, RLS-алгоритм, линейно-ограниченная адаптивная фильтрация, комплексные вычисления, действительные вычисления.

I. ВВЕДЕНИЕ

Адаптивные антенные решетки (ААР) сегодня все чаще используются в качестве антенн систем цифровой радиосвязи [1]. С помощью таких антенн обеспечивается не только прием полезного сигнала с известного направления, но и пространственная фильтрация помех, приходящих с неизвестных на приемной стороне направлений. Такая фильтрация осуществляется благодаря адаптивному формированию провалов в диаграмме направленности (ДН) антенной решетки в направлениях на источники помех.

Обычно для работы ААР, как разновидности многоканального адаптивного фильтра, требуется так называемый опорный сигнал [2,3]. Формирование этого сигнала часто является непростой задачей. Поэтому ААР, не требующие такого сигнала, являются привлекательными с практической точки зрения. Такие ААР обычно используют линейные ограничения, обеспечивающие требуемое значение уровня основного луча ДН в направлении источника полезного сигнала в случае, если это направление является известным [1], или используют свойство постоянного значения огибающей принимаемого полезного сигнала [5]. Каждый из этих приемов имеет свои недостатки, которые устраняются в случае совместного использования обоих приемов [6].

В настоящей работе рассматривается алгоритм адаптивной фильтрации сигналов с помощью ААР, аналогичный алгоритму [6], реализованный в арифметике действительных чисел.

II. ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ

Поскольку сигналы, принимаемые антеннами ААР, характеризуются относительными фазами, алгоритмы адаптивной фильтрации этих сигналов должны быть реализованы в арифметике комплексных чисел, что обуславливает примерно четырехкратное увеличение вычислительной сложности (числа арифметических операций, требуемых для выполнения одной итерации алгоритма) по сравнению с одноименными алгоритмами, обрабатывающими действительные сигналы. Однако, используя свойства симметрии, которые обычно присутствуют в антенных решетках, можно не только уменьшить результирующую вычислительную сложность адаптивных алгоритмов, но и улучшить их функциональные свойства.

В ААР любой конфигурации часто можно расположить антенны так, что они будут симметричными относительно фазового центра. В этом случае корреляционная матрица R_N входных сигналов ААР:

x_N(k)=[x₁(k), x₂(k),..., x_N-1(k),x_N(k)]^T=[x₁(k), x₂(k),..., x₂^*(k),x₁^*(k)]^T

является персимметричной эрмитовой матрицей, где x_n(k) – сигнал, принимаемый n – й антенной; k – номер отсчета этого сигнала (в информационной полосе частот); N – число антенн в решетке. Элементы, симметричные относительно главной диагонали, в такой матрице являются комплексно сопряженными по отношению друг к другу, а элементы, симметричные относительно побочной диагонали, – одинаковыми.

В большинстве адаптивных алгоритмов корреляционная матрица оценивается на возрастающем окне отсчетов, т.е. на всем интервале работы адаптивного фильтра как:

где K – число отсчетов сигналов, принимающих участие в формировании оценки этой матрицы. Для стационарных сигналов справедливо, что 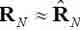при K → ∞.Такое оценивание называется прямым усреднением.

В работе [7] было показано, что использование прямого-обратного усреднения:

при оценке персимметричной эрмитовой корреляционной матрицы приводит к улучшению адаптивного формирования ДН ААР, так как 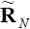является лучшей оценкой матрицы R_N по сравнению с 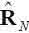в терминах расстояния:

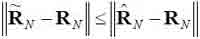
Здесь и далее J_N перестановочная матрица.

Кроме того, в работе [7] было показано, что использование матрицы 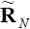позволяет также уменьшить вычислительную сложность обобщенного компенсатора боковых лепестков – одной из разновидностей алгоритмов адаптивной фильтрации, применяемых в ААР. Этот результат достигается за счет комплексно-сопряженной симметрии переменных, участвующих в вычислениях. Используя предварительное преобразование этих переменных, можно затем выполнять большую часть операций адаптивного алгоритма в арифметике действительных чисел. При этом сложность такого алгоритма является меньшей, чем в исходном алгоритме в арифметике комплексных чисел, использующем оценку корреляционной матрицы 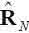, полученную прямым усреднением.

В настоящей работе приводится вычислительная процедура линейно-ограниченного многоканального алгоритма по критерию наименьших квадратов (Recursive Least Squares, RLS) адаптивной фильтрации сигналов с помощью ААР с симметричным расположением антенн. Алгоритм получен с помощью приемов, рассмотренных в работах [6-9].

Для использования приемов [6-9] необходимо, чтобы весовые коэффициенты ААР обладали комплексно-сопряженной симметрией относительно ее фазового цента. Для адаптивного алгоритма [6] наличие или отсутствие такой симметрии является неочевидным.

В работе [6] было показано, что в ААР с симметричным расположением антенн симметричные весовые коэффициенты вектора h_N(k), вычисляемого с помощью линейно-ограниченного RLS-алгоритма [6], использующего корреляционную матрицу 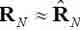являются комплексно сопряженными.

Поэтому, если в этом алгоритме использовать предварительное преобразование обрабатываемых сигналов с помощью матрицы:

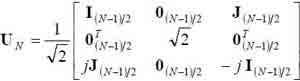
при нечетных N [6], то можно получить математически эквивалентный линейно-ограниченный RLS-алгоритм для вычисления весовых коэффициентов симметричной ААР, большинство операций в котором будут выполняться в арифметике действительных чисел.

С учетом особенностей применения этого алгоритма при обработке сигналов с постоянным значением комплексной огибающей, например с Phase Shift Keying (PSK) модуляцией, была получена вычислительная процедура адаптивного линейно-ограниченного RLS-алгоритма в арифметике действительных чисел, представленная ниже.

Определение переменных c_N и f, с помощью которых можно задать линейное ограничение на значение ДН ААР в направлении источника полезного сигнала, приведены в ряде литературных источников, в частности в [6]. Переменная y(k) обозначает выходной сигнал ААР, s²=const – квадрат модуля информационных символов полезного сигнала, δ² – параметр начальной регуляризации обращения корреляционной матрицы. Символом 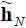(k) обозначен вектор весовых коэффициентов ААР, в котором симметричные элементы являются комплексно-сопряженными.

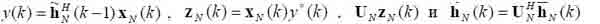
выполняются в арифметике комплексных чисел. Остальные операции алгоритма – действительные. Соответствующие действительные переменные, участвующие в этих операциях, обозначены прямой чертой сверху. Переменная f является действительной для алгоритмов обоих типов (с комплексными или действительными вычислениями).

В рассматриваемом алгоритме действительная матрица из-за прямого-обратного усреднения на каждой итерации по времени k обновляется дважды. В этом обновлении участвуют преобразованные векторы 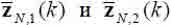. Поэтому, подобно RLS-алгоритмам с оценкой корреляционной матрицы на скользящем окне [9], все вычислительные процедуры в рассмотренном алгоритме и в алгоритме расчета коэффициентов Калмана требуется выполнять дважды. Как следствие, результирующие алгоритмы состоят из двух однотипных групп последовательно выполняемых вычислений, в которых используются или только переменные > или только переменные .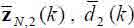

Пример вычисления векторов 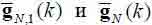с помощью обратного QR-разложения с операциями извлечения квадратного корня приведен ниже.

Здесь λ – параметр экспоненциального взвешивания обрабатываемых сигналов [9].

Полная сложность рассмотренного RLS-алгоритма определяется вычислениями, которые выполняются как в комплексной арифметике, так и в действительной арифметике. Сложность указанных выше комплексных вычислений равна 5N комплексным операциям умножения и 5N комплексным операциям сложения. Остальные вычисления алгоритма – действительные. Их сложность в части, связанной с линейными ограничениями, равна 6*N*J²+10*N*J+2*J²+2*J+4*N действительным операциям умножения, 6*N*J²+|12*N*J+8*J+6*N действительным операциям сложения и двум действительным операциям деления. Это оценка не учитывает вычисления векторов коэффициентов Калмана .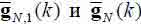

Вычисления векторов коэффициентов Калмана со- держит 2N действительных операций извлечения квадратного корня, которые обусловлены вычислени- ем переменных b_N(k) в течение N шагов i=1,...,N на каждой итерации алгоритма адаптивной фильтрации. Кроме того, эти вычисления содержат 5.5*N²+17.5*N действительных операций умножения, 3*N²+9*N действительных операций сложения и 2N операций деления.

При реализации аналогичного алгоритма в арифметике комплексных чисел, оценка его сложности (в терминах комплексных операций) также определяется приведенными выше уравнениями с коэффициентом, примерно равным 0.5, так как в комплексных алгоритмах используется только прямое усреднение корреляционной матрицы. Без учета операций, отсутствующих в комплексном варианте алгоритма, вычислительная сложность нового алгоритма примерно в 2 раза меньше, чем у его комплексного аналога, так как одна комплексная операция умножения со сложением содержит четыре действительные операции умножения и четыре действительные операции сложения. Это сравнение свидетельствует о примерно двукратной вычислительной эффективности полученного алгоритма по сравнению с его комплексным аналогом.

III. ЗАКЛЮЧЕНИЕ

Работоспособность полученного алгоритма адаптивной фильтрации подтверждена с помощью компьютерного моделирования ААР. На рис. 1 приведен пример моделирования процесса подавления одной помехи (белого шума), источник которой располагался в направлении максимума первого бокового лепестка ДН 8-элементной линейной эквидистантой ААР. Линии 1 и 2 показывают, что благодаря линейному ограничению уровень основного лепестка ДН поддерживается постоянным в течение всего процесса адаптации как в комплексном алгоритме, так и в алгоритме, рассмотренном в настоящей работе. Достигаемая глубина ДН в направлении источника помех в новом алгоритме в среднем на 2-4 дБ больше (кривая 3), чем в комплексном (кривая 4), а одинаковые значения ДН в течение переходного процесса достигаются за 1.5-2 раза меньшее время.

ЛИТЕРАТУРА

1. Джиган В.И. Адаптивные антенные решетки для систем цифровой связи: проблемы и их решение // «III Всероссийская научно-техническая конференция «Проблемы разработки перспективных микро и наноэлектронных систем (МЭС-2008)». Сборник трудов». (Москва, 6 – 10 октября 2008 г.). Москва, 2008. C. 472–475.
2. Пистолькорс А.А, Литвинов О.С. Введение в теорию адаптивных антенн. М.: Наука, 1991. 200 с.
3. Farhang-Boroujeny B. Adaptive filters theory and applications. John Willey & Sons, 1999. 548 p.
4. Frost O.L. An algorithm for linearly constrained adaptive array processing // Proceedings of the IEEE. 1972. Vol. 60. № 8. P. 926–935.
5. Treichler J., Larimore M. New processing techniques based on the constant modulus adaptive algorithm // IEEE Trans. Acoustics, Speech and Signal Processing. 1985. Vol. 33. № 2. P. 420–431.
6. Джиган В.И. Одновременное использование нескольких критериев в адаптивных антенных решетках // Доклады 10-й Международной конференции «Цифровая обработка сигналов и ее применения (DSPA-2008)», (Москва, 26 – 28 марта 2008 г.). Москва, 2008. Том 1. С. 168–172.
7. Nitzberg R. Application of maximum likelihood estimation of persymmetric covariance matrices to adaptive processing // IEEE Trans. Aerospace and Electronic Systems. 1980. Vol. 16. № 1. P. 124–127.
8. Huarng K.-C., Yeh C.-C. Adaptive beamforming with conjugate symmetric weights // IEEE Trans. Antennas and Propagation. 1991. Vol. 39. № 7. P. 926–932.
9. Джиган В.И. Многоканальные RLS- и быстрые RLS-алгоритмы адаптивной фильтрации // Успехи современной радиоэлектроники. 2004. № 11. С. 48–77.
10. Джиган В.И. Вычислительно эффективный линейно-ограниченный комплексный RLS-алгоритм в арифметике действительных чисел // Доклады 14-й Международной конференции «Цифровая обработка сигналов и ее применения (DSPA-2012)». (Москва, 28 – 30 марта 2012 г.). Москва, 2012. Том 1. С. ХХ–ХХ.