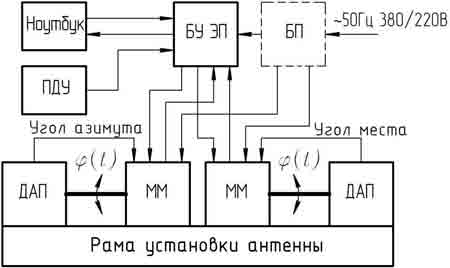
Рисунок 1 – Функциональная схема мехатронной системы (разработана авторами)
Авторы:
Громаков Е.И., Касымов К.Ш., Наумовская А.А., Терехов С.А.
Источник: Интернет-журнал «НАУКОВЕДЕНИЕ» https://naukovedenie.ru, Том 9, №5 (сентябрь – октябрь 2017), https://naukovedenie.ru/PDF/66TVN517.pdf, publishing@naukovedenie.ru
В работе выполнен анализ динамических характеристик мехатронной системы управления антенной, осуществляющей слежение за перемещением оптически ненаблюдаемого небесного объекта с использованием MatLab-моделирования. Отслеживание таких объектов возможно при условии знания их эфемерид. Из общих требований, предъявляемых к электроприводам систем автоматического управления, основными являются требования минимума статической и динамической ошибок позиционирования антенного устройства. При эксплуатации систем слежения в удаленных местах с трудностями обеспечения их электрической энергией дополнительным требованием является сокращение ее потребления. Для снижения электропотребления необходимо уменьшать колебания антенны в режиме слежения. Из-за непостоянства орбитальной скорости слежения небесного объекта, конечной жесткости кинематики мехатронной системы и ветровой нагрузки возникает отклонение скорости поворота антенны от требуемой на интервале времени между заданиями для отслеживания антенной соседних значений эфемерид небесного объекта. Это приводит к накоплению ошибки позиционирования в конце временного интервала движения антенны, которая будет тем больше чем реже заданы значения эфемерид. Поэтому период заданий эфемерид для слежения за небесным объектом должен быть приведен в соответствие с требуемой точностью позиционирования.
антенна; слежение; небесный объект; электропривод; мехатронный модуль; вентильный двигатель; люфт; волновой редуктор; пропорционально-интегрально-дифференцирующий регулятор; прогнозирование; энергоэффективность; моделирование.
В астрономических приложениях используются системы слежения за естественными и рукотворными небесными объектами. Многие из таких систем слежения работают в непрерывном режиме и могут располагаться в труднодоступных местах их эксплуатации. Часто эти системы снабжаются специальными типами электроприводов, которые отличаются важными особенностями:
Анализу динамических характеристик электроприводных систем слежения различного назначения посвящен ряд работ [2,4-6]. С помощью таких антенн обеспечивается не только прием полезного сигнала с известного направления, но и пространственная фильтрация помех, приходящих с неизвестных на приемной стороне направлений. Такая фильтрация осуществляется благодаря адаптивному формированию провалов в диаграмме направленности (ДН) антенной решетки в направлениях на источники помех.
Задача высокоточного отслеживания положения небесного объекта (с погрешностью в пределах 10 угловых минут), с использованием таблиц эфемерид наталкивается на трудности, связанные с синхронизацией угловой скорости поворота оси электропривода со скоростью прохождения небесного объекта на небосводе в течение интервала времени между соседними табличными значениями эфемерид. Из-за непостоянства орбитальной скорости слежения небесного объекта, перемещающегося по эллиптической орбите и ветровой нагрузки, возникает отклонение скорости поворота антенны от требуемой на интервале времени между заданиями для отслеживания антенной соседних значений эфемерид небесного объекта. Из-за моментов возмущения и неточностей кинематики электропривода антенны абсолютной синхронизации достичь невозможно. Поэтому при выборе компонентов системы слежения для обеспечения приемлемой точности позиционирования антенны в течение интервала времени между заданными соседними значениями таблицы эфемерид, необходимо выполнять учет наиболее существенных факторов, влияющих на точность позиционирования антенны.
Целью данной работы является анализ влияния на погрешность позиционирования антенны динамических характеристик мехатронной системы, осуществляющей слежение за перемещением небесного объекта на основе его координат, задаваемых таблицей эфемерид.
Исследуемая мехатронная система (рис. 1) относится к электроприводу согласованных поворотов антенны по двум осям углов азимута и места.

Рисунок 1 – Функциональная схема мехатронной системы (разработана авторами)
В состав мехатронной системы входят следующие основные компоненты:
Мехатронные модули отрабатывают текущие координаты по командам от БУ ЭП. БУ ЭП обеспечивает синхронные и согласованные повороты обоих ММ посредством электрических двигателей.
Операторно-структурная схема системы слежения с учетом конечной жесткости узла соединения рамы антенны с выходным валом мехатронного модуля представляет собой типовую двухмассовую систему электропривода с упругой механической связью (рис. 2).

Рисунок 2 – Операторно-структурная схема системы управления антенной (разработана авторами)
В исследуемой схеме слежения: s – оператор Лапласа φ3, φ – заданное и фактическое значение угла поворота одной из осей электропривода; φд' – угол закручивания выходного вала, вызванный его конечной жесткостью; ωд, ω, nр – угловая скорость вала двигателя и выходной оси электропривода, рабочая угловая скорость; δy, δc – ошибки электропривода по углу и по скорости; U – управляющее напряжение; i – передаточное число редуктора; J – момент инерцииустройства слежения; C, χ – коэффициент жесткости и диссипативных потерь в кинематике нежесткого соединения редуктор-антенна; Mв – момент внешних сил, в частности, момент, вызванный ветровой нагрузкой; Прп(s), Прс(s) – передаточные функции регулятора положения и регулятора скорости; БЗС – блок задания скорости двигателя.
Предрасположенность такой системы слежения к возникновению автоколебаний в установившемся режиме, вызванных конечной жесткостью крепления антенны к оси электропривода, не только создают значительные трудности по обеспечению необходимой динамической точности позиционирования и плавности движения, но и приводит к постоянному нецелевому расходу энергии электрическими двигателями. Дополнительным фактором ухудшения динамических характеристик системы слежения является зазор, вызванный люфтом редуктора [10]. С учетом наличия люфта в кинематической цепи электропривода MatLab – модель системы слежения имеет вид, показанный на рисунке 3. Здесь заданием являются интерполяционные значения углов программного наведения в предположении равноускоренного перемещения небесного объекта между соседними значениями эфемерид.
Пути совершенствования следящих приводов антенн такого применения следует искать в классе автоматических систем, алгоритмически обеспечивающих высокую точность отслеживания антенной эфемерид небесных объектов. Анализ динамических характеристик электроприводов мехатронной системы, осуществляющей слежение за перемещением небесного объекта на основе его координат, задаваемых таблицей эфемерид алгоритму управления системы слежения удобно выполнять в программной среде моделирования MatLab [3,9]. Показанная на рисунке 3 модель системы слежения за перемещением небесного объекта разработана в системе Simulink для следующих численных значений кинематики привода: люфт – 1 мин.; жесткость соединения – 1010 нм/рад; коэффициент диссипативных потерь в узле нежесткого крепления антенны – 10 нм сек./рад; момент инерции панели – 600 кг•м2.

Рисунок 3 – Модель системы слежения (разработана авторами)
Приемлемая точность позиционирования антенного устройства и снижение энергопотребления в динамическом режиме работы электропривода следящих систем достигается соответствующим выбором параметров регуляторов положения и скорости электропривода. В качестве регуляторов положения и скорости в системе слежения были выбраны классические изодромные регуляторы, настройка которых выполнялась с помощью модифицированного метода Циглера-Никольса и CHR-метода.
Наиболее подходящими для применения в автономных системах слежения небесных объектов при ограничениях потребления электрической энергии являются вентильные двигатели [1]. Для этого типа двигателей конструктивно можно добиться меньшего потребления энергии при одном том же уровне мощности нагрузки. Приемлемая величина мощности двигателя была ограничена 120 Вт, которая обеспечивает расчетный статический крутящий момент 16 000 Нм при передаточном отношении редуктора равном 21000. Такое решение, хотя и обеспечивает приемлемую мощность энергопотребления, создает опасность снижения жесткости кинематических узлов электропривода, вызванного большими размерами редуктора, устанавливаемого на валу двигателя маленьких размеров. Для снижения влияния люфта на точность позиционирования был выбран волновой редуктор, который по публикациям, например [10], может быть безлюфтовым
.
Модель вентильного двигателя, используемого в электроприводе антенны в среде MatLab, показана на рисунке 4.
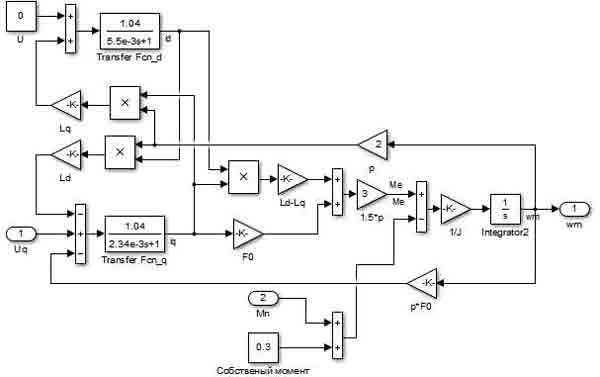
Рисунок 4 – Модель вентильного двигателя мощностью 120 ВТ (разработана авторами)
На рисунке 5 показаны графики изменений ошибок позиционирования и скорости вращения двигателя при изменении жесткости конструкции, значение которой приведены в верхнем правом углу диаграммы. Возникающая колебательность ведет к появлению рассинхронизации скорости поворота оси электропривода и скорости прохождения объекта слежения по небосводу. Любопытно то, что амплитуда колебаний ошибки позиционирования остается практически постоянной с увеличением жесткости, в то время как амплитуда колебаний скорости уменьшается, а это ведет к уменьшению потребления энергии электрическим двигателем в установившихся режимах слежения.
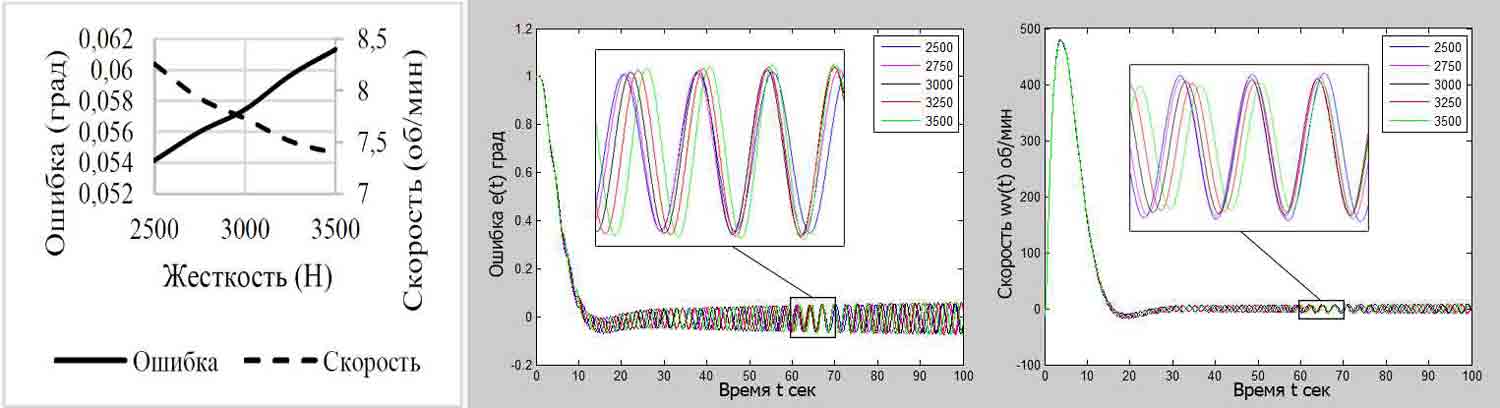
Рисунок 5 – Зависимость ошибок позиционирования и скорости при различной жесткости конструкции (составлено авторами)
Еще одним неблагоприятным фактором, влияющим на точность позиционирования, является моментная нагрузка на выходном валу электропривода. На рисунке 6 показаны графики изменений динамической ошибки позиционирования и ошибки скорости вращения двигателя при увеличении момента нагрузки, вызванной ветром [7]. Из диаграмм следует, что амплитуды установившихся колебаний ошибки позиционирования и скорости растут с увеличением ветровой нагрузки линейным образом.
Из теории автоматических систем известно [8], для снижения влияния нагрузки на валу электропривода на точность позиционирования антенного устройства следует использовать изодромный регулятор положения и скорости, что обеспечивает астатизм контуров регулирования и скорости и положения. Результаты модельных испытаний подтвердили возможность снижения, и колебательности, и погрешности до приемлемых величин путем подбора коэффициентов изодромных регуляторов скорости и положения.

Рисунок 6 – Зависимость ошибки позиционирования и ошибки скорости двигателя при различных моментах нагрузки (составлено авторами)
В момент восхода небесный объект двигается по отношению к наблюдателю с малой скоростью. Но по мере восхождения его угловая скорость относительно наблюдателя (скорость кажущегося движения на небесной сфере) быстро растет, причем нарастание скорости будет тем стремительнее, чем ниже пролегает его орбита. Так как в режиме программного наведения для управления приводом следящей системы линейная интерполяция при ускоренном перемещении между двумя соседними значениями эфемерид небесного объекта формирует непрерывное изменение задания скорости и углов положения, то динамика его изменения может повлиять на погрешность слежения.
Действительно, в этом случае появляется скоростная ошибка. Поэтому классический изодромный регулятор не может обеспечить нулевую статическую ошибку слежения. А это в свою очередь приводит к появлению погрешности позиционирования антенны в течение интервала времени между заданными соседними значениями таблицы эфемерид и, следовательно, возникает опасность недостижения требуемой точности слежения. Из теории автоматического регулирования известно, что для устранения скоростной ошибки следящей системы следует использовать ПИ2Д – регулятор с двойной интегрирующей составляющей, что обеспечивает астатизм контура автоматического регулирования даже при условии постоянного изменения скорости. Однако, использование такого регулятора оказывается проблематичным при настройке даже в модельном исследовании. Поэтому было выбрано решение по уменьшению временного интервала обновления значений эфемерид до нескольких секунд. Это позволило уменьшить ошибку слежения до приемлемой величины.
Из-за неблагоприятных факторов, связанных с непостоянством орбитальной скорости наблюдения небесного объекта и ветровой нагрузки возникает отклонение скорости поворота антенны от требуемой на интервале времени между заданиями отслеживания антенной соседних значений эфемерид небесного объекта. Это приводит к появлению скоростной ошибки позиционирования в конце временного интервала. Для снижения влияния этих факторов был выбран регулятор скорости, обеспечивающий астатизм контуров регулирования положения антенны и скорости электропривода системы слежения.
Возникновение колебаний скорости электрического двигателя из-за конечной жесткости узла соединения антенны с редуктором и из-за наличия люфта в редукторе приводит к дополнительному непрерывному расходу энергии в установившемся режиме слежения антенного устройства, вызванному периодическим разгоном двигателя с последующим его торможением. Такая колебательная динамика негативно влияет на энергоэффективность работы системы, так как часть энергии теряется на непроизводительную работу электропривода. Модельные исследования показали, что посредством подбора коэффициентов регуляторов, амплитуду этих колебаний можно уменьшить и тем самым обеспечить снижение потребление энергии электроприводом антенного устройства.
Для обеспечения приемлемой точности позиционирования антенны необходимо увеличивать жесткость кинематики электропривода, и конструктивно усиливать жесткость узлов крепежа антенны, что позволяет снижать амплитуду и увеличивать частоту колебаний антенны в режиме слежения. Последнее является необходимым требованием к динамике электропривода при уменьшении временного интервала обновления значений эфемерид.