Рисунок 1
Авторы: Иванченко А. Я.
Источник: Казанский национальный исследовательский технический университет имени А. Н. Туполева КАИ, К. Маркса, 10, Казань, 420111, Россия,
https://www.researchgate.net/publication/311486331_Using_an_adaptive_tuning_PID_controller_for_a_radar_antenna, e-mail: alesiaiwn@mail.ru
Задача заключается в разработке адаптивной системы управления антенной радиолокационной станции на базе классического пропорционально–интегрально–дифференциального (ПИД) регулятора с применением таких современных технологий управления, как нечёткое управление. Необходимость адаптивной настройки возникла в связи с тем, что классический регулятор обладает высокой чувствительностью к возмущениям входного сигнала, необходимостью ручной настройки параметров регулятора и, в связи с этим, необходимостью частой перенастройки регуляторов, а также невозможностью обеспечения оптимальных характеристик регулятора для процессов с нелинейностями или изменяющимися с течением времени параметрами.
система управления, управление антенной радиолокатора, адаптивная настройка регулятора, ПИД регулятор, адаптивная настройка ПИД регулятора, управление антенной РЛС, адаптивная система управления
В своей речи от 14 июня 2012 года, президент Российской Федерации Владимир Владимирович Путин заявил: В ближайшие пять лет должен быть реализован проект дальнего радиолокационного обнаружения А-100
. Системы дальнего радиолокационного обнаружения и управления расположенные на летательном аппарате (чаще всего это самолёт) называют авиационными комплексами радиообнаружения и наведения (в англоязычной литературе Авиационная система раннего предупреждения и управления
), и необходимы для осуществления обнаружения объектов. Подобные системы предназначены для разведки и управления воздушным боем, однако могут быть использованы и для
При повышении требований к авиационным комплексам радиообнаружения и наведения, повышаются требования и к наземным системам обнаружения и наведения, коими являются радиолокационные станции (РЛС). Антенна радиолокатора (антенна РЛС), систему управления которой предлагается разрабатывать, расположена в боевом положении на крыше фургона. Для обеспечения высокой точности наведения при определении дальности, скорости и геометрических параметров воздушных, морских и наземных объектов необходимо реализовать вращение антенны по азимуту с достаточно большими угловыми скоростями, а для этого систему управления антенной РЛС предлагается сделать адаптивной.
Анализ принципов построения традиционных систем управления антенной радиолокатора показал, что они имеют ряд недостатков. Среди них можно выделить такие как: не выполнение условий согласования, когда точки приложения возмущения и управления не совпадают; неполнота информации о векторе состояния системы, когда управление осуществляется по измеряемым выходным координатам системы; использование блока идентификации динамики объектов управления, особенно для систем высокого порядка, существенно усложняет структуру системы управления. При этом точность идентификации зависит от внешних воздействий, что осложняет задачу регулирования и в некоторых случаях может приводить к потере устойчивости. Потому, для управления антенной радиолокатора предлагается применять адаптивный (самонастраиваемый) ПИД регулятор. Адаптивная настройка будет осуществляться за сч.т неч.ткого регулирования параметрами усиления классического ПИД регулятора в зависимости от изменяющихся условий. Кроме того неч.ткий регулятор сможет обеспечить помехозащищ.нность, что важно для антенн РЛС, так как помехи могут стать причиной получения неточного сигнала.
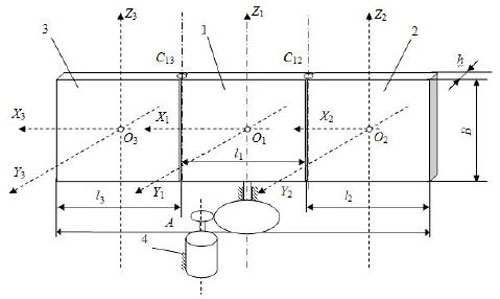
Необходимо разработать алгоритмы и программы анализа и синтеза системы управления поворотом нежесткой антенны РЛС. Антенна радиолокатора имеет следующие характеристики: A=1400мм; B=1200мм; h=130мм; l1=600мм; l1=23=400мм. Разрабатываемая система должна обеспечить высокую максимальную скорость поворота антенны (высокое быстродействие системы), а перерегулирование – необходимо осуществлять автоматически за счёт самонастройки системы, т.е. фактически, перерегулирование не должно занимать времени вообще.

Рисунок 1
Ж?сткость упругого элемента определяется в соответствии с собственной частотой колебаний, равной 2 Гц, а создание модели управляемого согласующего устройства осуществляется посредством применения пакета прикладных программ MatLab, а также некоторых его специальных инструментов (Control Systems Toolbox, Robust Control Toolbox, Fuzzy Logic Toolbox).
Для разработки системы автоматического управления антенной радиолокатора, как объекта управления, необходимо произвести расчёт математической модели антенны РЛС. При этом задать математическую модель можно двумя способами:
После изучения имеющихся способов задания математической модели, для данного объекта управления был выбран первый способ, где абстрактная математическая модель в форме вход-выход (с одинаковым числом входов и выходов) может быть представлена следующим символьным описанием объекта, являющимся единой формой описания стационарных линейных, нестационарных линейных и нелинейных объектов управления с сосредоточенными и распределёнными параметрами:
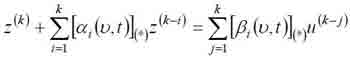
(1)
где z ∈ Rm, u ∈ Rm, z – вектор выхода; u – вектор входа; k – некоторое заданное положительное число; [αi(υ,t)](*), [βi(υ,t)](*) – заданные в символьном виде функциональные матрицы соответствующих размеров (см. [4]), индекс (*) представляет номер уравнения, которое задает область изменения аргументов уравнения (1).
В роли этих аргументов выступают время t и n-мерный вектор υ, подчиненный некоторому заданному уравнению (*). Таким образом, область изменения аргументов функциональных матриц задаётся посредством некоторого уравнения (*). Тем самым, абстрактная математическая модель, в отличие от общепринятых зада?тся не одним, а двумя уравнениями.
Нетрудно видеть, что степень многочлена правой части (1) может быть меньше k, но при этом соответствующие матрицы [βi(υ,t)](*) следует полагать нулевыми. Аналогично, в случае, когда размерности векторов входа и выхода не совпадают, нулевыми следует полагать соответствующие элементы матриц [αi(υ,t)](*), [βi(υ,t)](*).
Кинематическая схема модели антенны состоит из трех однородных по плотности прямоугольных пластин 1, 2, 3 средняя из которых жестко закреплена на валу привода, а две другие, связаны со средней, через упругий элемент с жесткостью c, массой m и размером A×B×h (рисунок 1). Жесткость упругого элемента определяется в соответствии с собственной частотой колебаний, равной 2Гц.
Рассматриваемая система имеет три степени свободы, которые определяются независимыми обобщенными координатами φ1, φ2, φ3 измеряемыми в неподвижной (инерциальной) системе координат O1X0Y0Z0 (рисунок 2).
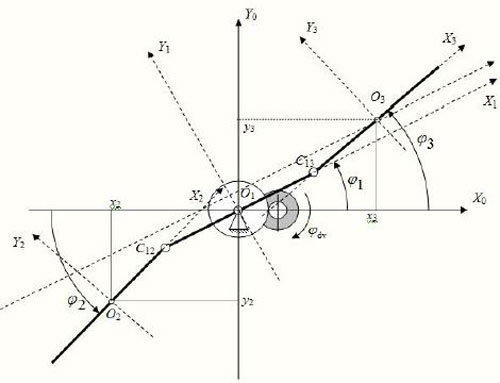
Рисунок 2
В рассматриваемой системе имеется несколько видов силовых воздействий:

(2)
С учётом (2) и других воздействующих на систему силовых воздействий было получено выражение обобщённых сил системы управления антенной:
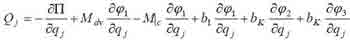
(3)
где j=1, 2, 3; b1 – силы, воздействующие на центральную пластину антенны; bK – силы, воздействующие на боковые пластины антенны. При этом стоит подчеркнуть, что момент сопротивления включает в себя, в том числе и момент сухого и вязкого трения, поэтому в дальнейших расчётах отдельно обозначаться не будет.
С учетом вышеприведённых расчётов, на основе уравнения Лагранжа 2-ого рода (4):

(4)
было получено уравнение движения антенны радиолокатора в виде (5):
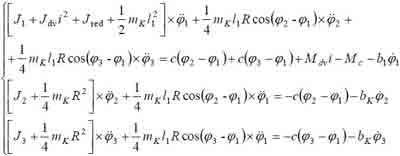 .
.(5)
Проанализировав исходные характеристики системы, было установлено, что замкнутая система является неустойчивой, что видно из логарифмической амплитудно-частотной характеристики (рисунок 3), где частота среза ωср лежит правее частоты ωpi, при которой угол фазового сдвига φ(ωср)=-180o, т.е. годограф амплитудно-фазовой характеристики на комплексной плоскости охватывает критическую точку с координатами (-1; j0).

Рисунок 3
После включения в систему пропорционально–интегрально–дифференциального регулятора, удалось добиться устойчивости системы, что видно из рисунка 4.

Рисунок 4
Проблема применения традиционного для таких систем ПИД регулятора заключается в том, что для подбора коэффициентов усиления обеспечивающих устойчивость системы, пришлось потратить много времени и, даже полученный результат, не удовлетворяет всем выставленным требованиям. Так время регулирования системы управления с классическим ПИД регулятором составляет около 2 секунд. Кроме того, в полученной системе очень велики колебания по углу и по скорости для боковых пластин антенны, что может сказаться на работе радиолокатора, потому предлагается осуществлять подстройку параметров ПИД регулятора нечётким регулятором.
Анализ принципов построения традиционных систем управления антенной РЛС базируется на классическом ПИД регуляторе. Однако из выше представленного материала видно, что он имеет ряд недостатков. Для управления антенной радиолокатора предлагается применить ПИД регулятор, коэффициенты усиления которого будут настраиваться при помощи нечёткого регулятора, т.е. основной функцией нечёткого регулятора будет автоматическая подстройка параметров усиления классического ПИД регулятора в зависимости от изменяющихся условий. Кроме того, нечёткий регулятор сможет обеспечить помехозащищённость, что важно для антенн РЛС.
Подстройка параметров ПИД регулятора может быть выполнена с помощью блока нечеткой логики (рисунок 5). Блок нечеткой логики (фаззи-блок) использует базу правил подстройки и методы нечеткого вывода. Фаззи-подстройка позволяет уменьшить перерегулирование, снизить время установления и повысить робастность ПИД регулятора [8].

Рисунок 5
Процесс автонастройки регулятора с помощью блока нечеткой логики начинается с поиска начальных приближений коэффициентов регулятора. Это делается обычно методом Зиглера-Никольса, исходя из периода собственных колебаний в замкнутой системе и петлевого усиления. Далее формулируется критериальная функция, необходимая для поиска оптимальных значений параметров настройки методами оптимизации.
Настройки регулятора осуществляется в несколько шагов [9]. Сначала выбирают диапазоны входных и выходных сигналов блока автонастройки, форму функций принадлежности искомых параметров, правила нечеткого вывода, механизм логического вывода, метод дефаззификации и диапазоны масштабных множителей, необходимых для пересчета четких переменных в нечеткие.
Поиск параметров регулятора выполняется методами оптимизации. Для этого выбирается целевая функция как интеграл от суммы квадратов ошибки регулирования и времени установления. В критерий минимизации иногда добавляют скорость нарастания выходной переменной объекта.
В качестве искомых параметров (параметров, которые надо найти) выбирают положение максимумов функций принадлежности (рисунок 6) и масштабные коэффициенты на входе и выходе фаззи-блока. К задаче оптимизации добавляют ограничения на диапазон изменения позиций функций принадлежности. Оптимизация критериальной функции может быть выполнена, например, с помощью генетических алгоритмов.

Рисунок 6
Если величина ошибки e на входе нечеткого регулятора (рисунок 5) равна e1 (см. рисунок 6), то соответствующее значение нечеткой переменной будет равно PS со степенью принадлежности подмножеству PS, равной μ(e1)=0.82, или равно PM со степенью принадлежности μ(e1)=0.18. Степень принадлежности ошибки e1 другим множествам ( Z, PL, NS и др.) равна нулю. Таким образом, величина ошибки e1 оказалась преобразованной в нечеткие переменные.
Нечеткий логический контроллер воспринимает информацию с двух входов (по ошибке и по производной ошибки) системы. На выходе нечеткого регулятора осуществляется настройка коэффициентов усиления Kp, Ki и Kd ПИД регулятора. Рисунок 7 показывает моделирования нечеткого регулятора, а рисунок 8 – Simulink блок нечеткого ПИД регулятора.

Рисунок 7
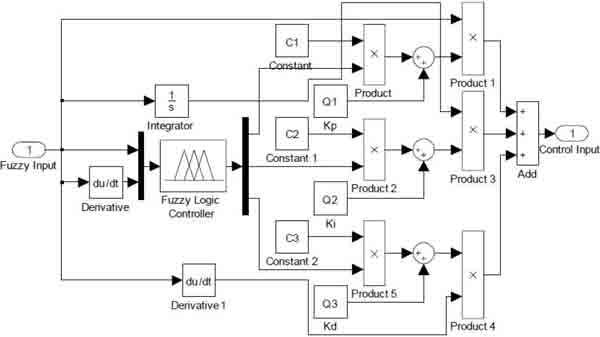
Рисунок 8
Применение нечеткого регулятора позволяет автоматически регулировать параметры усиления Kp, Ki и Kd ПИД регулятора. При этом происходит изменение передаточной функции объект управления (ОУ).
Результаты моделирования показывают, что реакция адаптивного нечеткого ПИД регулятора сравнительно лучше, чем классического ПИД регулятора. Также было замечено, что с увеличением порядка объекта управления, реакция ПИД регулятора становится скуднее. Хотя реакция адаптивного нечеткого ПИД регулятора является сравнительно лучше. Также мы видим, что адаптивный нечеткий ПИД регулятор дает превосходные результаты для объекта управления 2-го и 3-го порядка, по сравнению с другими высшими объектами управления. Данные эксперименты, дают основания полагать, что применение адаптивного нечёткого регулятора для управления антенной радиолокатор приведет к положительным результатам.