Назад в библиотеку

---

Новый метод бездатчикового определения скорости двигателя постоянного тока со щеточным коллектором

Авторы: Ernesto Vazquez-Sanchez, Joseph Sottile, Jaime Gomez-Gil
Автор перевода: Д.А. Тихонов
Источник: Multidisciplinary Digital Publishing Institute,  Appl. Sci., Volume 7, Issue 1 (January 2017, A Novel Method for Sensorless Speed Detection of Brushed DC Motors)

Реферат

Многие варианты применения электрических двигателей требуют точного измерения скорости. Для двигателей постоянного тока (ДПТ) со щеточным коллектором скорость может быть измерена с помощью обычных наблюдателей или бездатчиковых наблюдателей. Преимущество бездатчиковых наблюдателей в том, что они не требуют подключения внешних устройств к двигателю. Вместо этого измеряются напряжение и/или ток и используются для определения скорости. Бездатчиковые наблюдатели обычно делятся на две группы: те, которые основаны на динамической модели, и те, которые основаны на пульсирующей составляющей. В настоящей статье предлагается метод, основанный на измерении тока двигателя постоянного тока и анализе положение его спектральных компонентов. По этим спектральным компонентам, согласно предложенному методу, оценивается скорость двигателя. Три теста, каждый из которых был проведён со скоростями, варьирующимися от 2000 до 3000 об/мин, без изменения скорости, с плавным её изменением, либо с быстрым изменением, показали, что средняя ошибка составила менее 1 об/мин и что ошибка отклонения составила менее 1,5 об/мин. Предлагаемый метод: (I) является новым методом, не основанным ни на динамической модели, ни на пульсирующей составляющей; (II) требует лишь измерения тока якоря для определения скорости; (III) может быть использован для ДПТ со щеточным коллектором с большим количеством витков; и (IV) имеет малую погрешность при оценке скорости.

Ключевые слова: двигатель постоянного тока со щеточным коллектором; бездатчиковое управление; наблюдатель скорости; спектральный анализ; ток

1. Введение

Двигатели постоянного тока делят на две большие группы: щеточные и бесщеточные. Первая группа имеет щетки и коллектор, а вторая – нет. Преимущество щеточных ДПТ в том, что они легки в управлении. Поэтому раньше они были наиболее популярным типом двигателей, которые используются во многих случаях и по сегодняшний день. Щеточные ДПТ могут использоваться как в случае с низкой мощностью, так и с высокой. Обычно, маломощные щеточные ДПТ используются в быту, хотя также они могут использоваться в некоторых промышленных отраслях, например, в автомобильной промышленности. С другой стороны, мощные щеточные ДПТ в основном используются в промышленности.

Существует два типа наблюдателей для определения скорости щеточного ДПТ: обычные наблюдатели и бездатчиковые наблюдатели. Обычными наблюдателями являются такие устройства, как энкодеры, тахометры, датчики на эффекте Холла и др. Это независимые устройства, крепящиеся в валу двигателя. Следовательно, они могут быть источником сбоев, они увеличивают стоимость и требуют обслуживания [1]. Бездатчиковые наблюдатели – это алгоритмы, которые оценивают скорость и/или положение двигателей основываясь на сигналах напряжения или тока двигателя.

Основными преимуществами бездатчиковых наблюдателей являются: отсутствие необходимости в их обслуживании, уменьшение количества соединений, снижение стоимости системы и её компактность.

Бездатчиковые наблюдатели для измерения скорости двигателя делятся на две группы [2]: основанные на динамической модели и основанные на пульсирующей составляющей:

• Наблюдатели, основанные на динамической модели, оценивают скорость используя математическую модель ДПТ. Обычно используется линейная модель [3,4], но недостаток такого подхода заключается в том, что используемые параметры, такие как активное сопротивление, индуктивное сопротивление и противо-ЭДС, изменяются при различных условиях работы [5,6]. В такой ситуации, параметры настроены для одного условия работы и не изменяются. Следовательно, наблюдатели работают корректно, когда рабочие условия схожи с указанными, но работают некорректно, когда рабочие условия отличаются от указанных. Одним из решений этой проблемы является использование динамической адаптации параметров модели [7,8,9], однако это приводит к значительному усложнению модели, которая, как правило, имеет нелинейный характер. Еще одним решением является использование нелинейной модели щеточного ДПТ [10,11,12] или технология, которая косвенно моделирует двигатель, например, нейросеть [13,14] и фильтр Калмана [15,16]. Недостаток этих подходов в том, что они требуют большой вычислительной мощности, а адаптация параметров – это довольно трудная задача. Третьим решением является метод с простой моделью, которая справедлива только для определенных условий. Например, такой метод может смоделировать двигатель только при отключенном питании [17]. Недостаток такого подхода заключается в том, что скорость может быть измерена только при выполнении определенного условия.
• Наблюдатели, основанные на пульсирующей составляющей, используют часть сигнала переменного тока, которая называется пульсирующей составляющей [2,18]. Эта составляющая является результатом двух эффектов. Первый эффект возникает потому, что противо-ЭДС, наводимая в каждом витке имеет синусоидальную форму и выпрямляется щеточно-коллекторной системой неидеально [19]. Второй эффект возникает из-за того, что щетки иногда создают короткое замыкание двух смежных сегментов коллектора, соединяющие клеммы витков, соединенных с этими сегментами коллектора, что приводит к возникновению пиков в сигнале тока [20]. Оба эффекта приводят к пульсациям в сигнале тока. Количество пульсаций в секунду, или пульсирующая составляющая, связана со скоростью двигателя [21]. Многие методы в литературе используют пульсирующую составляющую [2,18,22,23,24,25].

Выявление пульсаций в бездатчиковом наблюдателе, основанном на пульсирующей составляющей, может быть сложным из-за шума [26]. Шум создаёт призрачные пульсации, которые являются ненаблюдаемыми пульсациями пульсирующей составляющей. Также шум создаёт ложные пульсации, которые являются пульсациями в токе, которые не относятся к пульсирующей составляющей тока. Существуют исследования, которые определили призрачные пульсации и отбросили ложные пульсации [27,28], но используемые методы были сложны и требовали большой вычислительной мощности.

Пульсирующая составляющая напрямую зависит от количества витков в двигателях, потому что эта составляющая возникает в процессе выпрямления тока в щеточно-коллекторной системе. Следовательно, если количество витков в двигателе мало, то процесс выпрямления в щеточно-коллекторной системе далёк от идеального, в то время как, в случае с большим количеством витков, процесс выпрямления близок к идеальному, другими словами, имеет лишь постоянную составляющую. В таком случае, бездатчиковые наблюдатели, основанные на пульсирующей составляющей, могут быть использованы лишь в ДПТ с малым количеством витков, например, дробные двигатели мощностью до 1 л.с., потому что пульсирующая составляющая в них достаточно велика, чтобы определить её. И наоборот, бездатчиковые наблюдатели, основанные на пульсирующей составляющей, не могут использоваться в ДПТ с большим количеством витков, потому что пульсирующая составляющая недостаточно велика, чтобы определить её.

В настоящей статье представлен новый метод, основанный на измерении тока щеточного ДПТ и анализе положение его спектральных составляющих с целью определения скорости двигателя. Этот метод может использоваться в двигателях с большим количеством витков, таких как интегральные ДПТ мощностью свыше 1 л.с. Раздел 2 описывает различные спектральные компоненты, присутствующие в токе, и устанавливает, какие из них важны в двигателях с малым количеством витков, как в дробных ДПТ, и какие из них важны в двигателях с большим количеством витков, как в интегральных ДПТ. В разделе 3 представлен предлагаемый бездатчиковый метод определения скорости щеточного ДПТ. В разделе 4 описаны эксперименты, проведенные для проверки этого метода. Наконец, в разделе 5 представлены выводы, сделанные в результате этого исследования.

2. Спектральные составляющие тока щеточного ДПТ

Напряжение и ток двигателя постоянного тока имеют две разные спектральные составляющие: постоянную и переменную. Постоянная составляющая производится источником питания. Переменная составляющая в основном производится противо-ЭДС, наводимой в обмотке. Противо-ЭДС это напряжение, прибавляемое к напряжению ДПТ.

На рисунке 1 показан реальный двигатель постоянного тока и эквивалент Тевенина для источника питания, питающего двигатель. Источник питания смоделирован согласно эквивалентной цепи Тевенина с идеальным источником и последовательным сопротивлением, где V_cc это источник идеального напряжения, а R_s это последовательное сопротивление. Исходя из этого, зависимость между напряжением V_m и током I_m щеточного ДПТ можно выразить следующим образом:

(1)

Рисунок 1 – Эквивалентная схема Тевенина для источника напряжения и двигателя постоянного тока

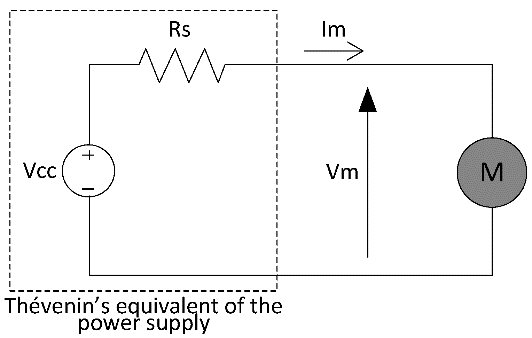
Следует отметить два момента, исходя из уравнения (1). Во-первых, поскольку V_cc и R_s являются постоянными, ток и напряжение двигателя будут связаны друг с другом и каждая составляющая напряжения будет также присутствовать в токе. Во-вторых, значение R_s обычно мало, а V_cc подобно V_m. Таким образом, величина спектральных составляющих тока по сравнению с величиной постоянной составляющей тока будет больше, чем величина спектральных составляющих напряжения по сравнению с величиной постоянной составляющей напряжения. Следовательно, измерение токовых спектральных составляющих будет проще, чем измерение спектральных составляющих напряжения. Затем спектральные компоненты тока обычно используются для бездатчикового определения скорости двигателей постоянного тока вместо использования спектральных составляющих напряжения.

Характер спектральных составляющих будет описан в следующих двух подразделах.

2.1. Пульсирующая составляющая

Щеточные ДПТ имеют количество витков, B, в роторе, которые соединены с внешней цепью через щетки и коллектор. Согласно закону Фарадея, когда двигатель вращается, в каждом витке наводится противо-ЭДС. Эта противо-ЭДС выпрямляется щеточно-коллекторной системой и передаётся во внешнюю цепь. Противо-ЭДС и коммутация проходят в каждом витке так, что эти противо-ЭДС складываются и выпрямляются щетками и коллектором. В идеале выпрямление выдаёт постоянный сигнал во внешнюю цепь. Напротив, реальный процесс выпрямления производит небольшую переменную составляющую, складывающуюся с постоянным сигналом во внешней цепи. Эта переменная составляющая называется пульсирующей составляющей.

Амплитуда пульсирующей составляющей зависит от количества витков, их индуктивности и мощности двигателя. Частота пульсирующей составляющей зависит от количества пульсаций в секунду, возникающих в токе. Каждая пульсация возникает, когда виток находится напротив полюса двигателя. Этот магнитный полюс может быть или северным, или южным. Из-за выпрямления тока в коллекторе, нет разницы, какой именно это полюс.

Исследование, проведённое Baoguo et al. [21], связывает частоту пульсаций, f_r, с числом полюсов, 2p, числом сегментов коллектора, k, и скоростью двигателя, n, следующим образом:

(2)

где η – это наибольший общий делитель 2p и k.

Эта составляющая важна в двигателях постоянного тока с малым числом витков, как в дробных ДПТ, потому что амплитуда пульсирующей составляющей относительно велика [29].

Другие спектральные составляющие

Щеточные ДПТ состоят из двух цепей: якоря и цепи возбуждения. Взаимодействие магнитных полей, производимых каждой цепью, создаёт момент на роторе, что приводит к его вращению. Вращение происходит согласно законам Фарадея и Лоренца. Противо-ЭДС наводится согласно закону Фарадея, а момент возникает согласно закону Лоренца [30]. Согласно закону Фарадея, противо-ЭДС, наводимая в витке i двигателя, равна:

(3)

где магнитный поток, φ_i, в витке i равен:

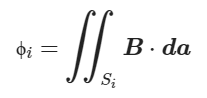(4)

а также B это – плотность магнитного потока, da – это оператор дифференцирования, а S_i, – это площадь витка i. Напряжение на щётке двигателя, V, это сумма выпрямленных напряжений всех витков:

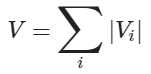(5)

Поскольку каждый виток и полюс в ДПТ уникальны, наводимое напряжение, связанное с каждым витком, V_i, имеет немного отличную форму сравнительно с напряжением других витков. Кроме того, фазы также различны, потому что положение каждого витка в роторе отличается от остальных. Из-за этого, согласно уравнению (5), противо-ЭДС на щётках, V, имеет характерную форму, повторяющуюся с каждым поворотом ротора. Период повторения обратен количеству оборотов в секунду двигателя и его частота равна скорости двигателя в оборотах в секунду. Можно использовать ряды Фурье для разложения сигнала V:

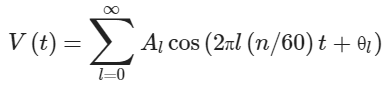(6)

где l – это индекс ряда Фурье, A_l и θ_l – это коэффициенты ряда Фурье, n/60 – это скорость двигателя в об/с, n – это скорость двигателя в об/мин [31]. Результат преобразования Фурье уравнения (6):

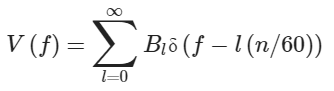(7)

где f – это частота, B_l – это комплексный коэффициент, зависящий от коэффициентов ряда Фурье A_l и θ_l, δ(⋅) – это дельта-функция Дирека. Согласно уравнению (7), спектр напряжения имеет разные спектральные составляющие с компонентой на каждой из следующих частот:

(8)

и расстояние между компонентами равно:

(9)

Как указано в разделе 2, ток и напряжение связаны, поэтому их спектры тоже связаны. Таким образом, каждый компонент спектра напряжения также присутствует в спектре тока и есть эквивалентное выражение из уравнений (6) – (9), применимое к току.

Частота пульсирующей составляющей кратна n/60 согласно уравнению (2), таким образом, она совпадает с частотой, определяемой способом, описанным в этом подразделе согласно уравнению (8). Частота пульсирующей составляющей соответствует индексу l = (2p ⋅ k)/η и это главная составляющая, относящаяся к скорости двигателя.

Из-за того, что каждое V_i незначительно отличается от остальных, изменения в напряжении и токе малы, как и веса коэффициентов A_l.

Спектральные компоненты, создаваемые этим эффектом, могут быть легко определены в токе, когда амплитуда пульсирующей составляющей равна амплитуде этих компонентов. Это случай для ДПТ с большим количеством витков, таких как интегральные ДПТ.

Пример спектра амплитуды тока реального интегрального ДПТ изображен на рисунке 2.

Рисунок 2 – Эквивалентная схема Тевенина для источника напряжения и двигателя постоянного тока

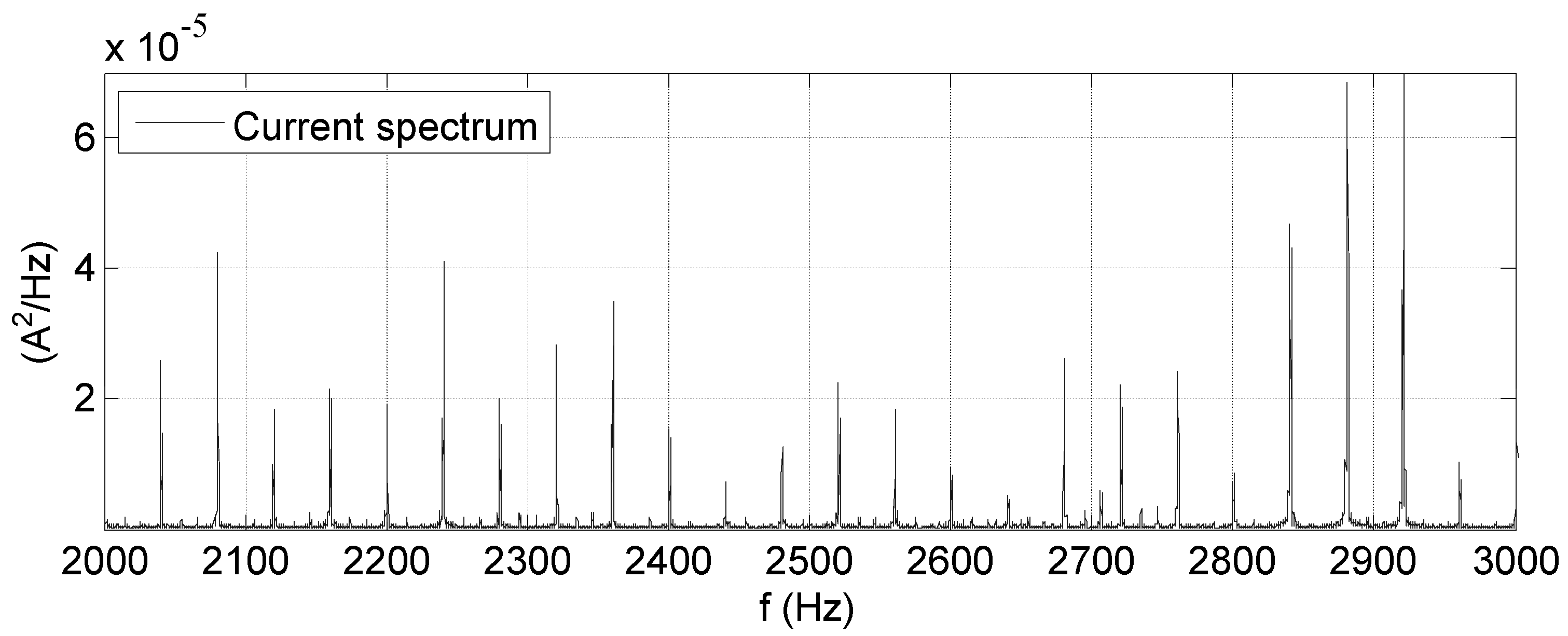
3. Предлагаемый метод

Настоящая статья представляет новый метод определения скорости щеточного ДПТ, используя спектральные составляющие тока двигателя. Этот метод был разработан для щеточных ДПТ с большим числом витков, таких как интегральные ДПТ, когда амплитуда компонентов схожа с амплитудой других составляющих, относящихся к скорости двигателя, см. раздел 2. Блок-схема предлагаемого метода, представленная на рисунке 3, включает в себя 5 блоков: буферный блок, блок определения df_m, блок отслеживания частоты, блок проверки и блок преобразования.

Рисунок 3 – Блок-схема предлагаемого метода определения скорости

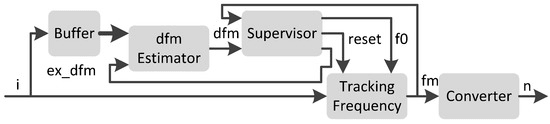
3.1. Буферный блок

Буферный блок (рис. 3) накапливает значения тока за предыдущие T_b секунд и выдаёт вектор последних значений, собранных за это время. На вход буферного блока приходит значение тока, i, а выходом является набор значений, которые были накоплены.

3.2. Блок определения df_m

Блок определения df_m делает первоначальное определение расстояния между частотами в спектре тока, которые относятся к скорости двигателя, df_m. Позже эта оценка используется последующими блоками для инициализации первой оценки положения одной частотной составляющей в спектре тока.

Этот блок (рис. 3) имеет два входных сигнала и один выходной. Входными являются вектор значений тока i, накопленный в буфере, а также сигнал ex_dfm, бинарное значение, которое показывает, должен ли быть выполнен этот блок. Когда переменная ex_dfm принимает значение True, блок выполняется, а когда принимает значение False, блок не выполняется. Когда блок выполняется, производится первоначальная оценка df_m.

Блок-схема блока оценки df_m, когда он активен, другими словами, когда значение ex_dfm равно True, показана на рисунке 4. Как показано, блоку вычисления df_m требуется несколько шагов для получения точного значения расстояния между частотами в спектре тока. Расстояние между частотами связано со скоростью двигателя.

Рисунок 4 – Блок-схема блока определения df_m, когда ex_dfm принмает значение True. FFT: быстрое преобразование Фурье

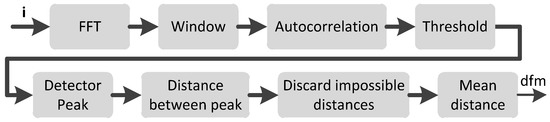
Блок определения df_m (рис. 3) выполняет быстрое преобразование Фурье (FFT) над вектором накопленных значений тока для получения его спектра. Тем не менее, не все составляющие спектра тока используются в алгоритме. Поэтому следующий блок выбирает частоты между f_min и f_max, которые используются в дальнейшем. Участок вне этого окна содержит значительный шум и будет мешать определению. Еще одной причиной, из-за которой не используются частоты вне этого окна, является то, что потребуется дополнительная вычислительная мощность в случае использования этих частот. Чтобы уменьшить влияние шума на определение расстояния между частотами, используется автокорреляция диапазона частот между f_min и f_max:

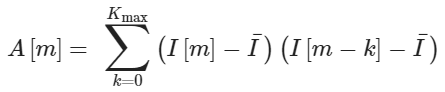(10)

где A[m] – это автокорреляция, I[m] – это спектр тока между f_min и f_max, I – это среднее значение спектра тока между f_min и f_max, K_max – это количество значений спектра между f_min и f_max, а m – это индекс дискреты. Эта формула автокорреляции необычна по причине того, что среднее значение предварительно отнимается от входного значения. Это действие исключает эффект среднего значения в автокорреляции и гарантирует, что базовый уровень автокорреляции не будет уменьшаться в то время, как индекс m будет расти. Это упрощает определение пиков в сигнале автокорреляции.

Сигнал автокорреляции имеет различные пики, связанные с расстоянием между частотами, присутствующими в спектре тока. Например, первый пик автокорреляции показывает расстояние между пиками в спектре сигнала, второй пик – это удвоенное расстояние, а третий пик – утроенное расстояние. Итак, расстояние между двумя последовательными пиками – это расстояние между частотами в спектре. Преимуществом использования сигнала автокорреляции вместо спектра является ослабление шума и, следовательно, более точное определение. Это можно увидеть на рисунке 5, на котором изображена амплитуда сигнала автокорреляции, полученного согласно предложенному методу, из спектра тока на рисунке 2. Скорость двигателя в этой ситуации равна 2400 об/мин и расстояние между частотами в спектре составляет 40 Гц согласно уравнению (9).

Рисунок 5 – Автокорреляция спектра тока, полученная согласно предложенному методу

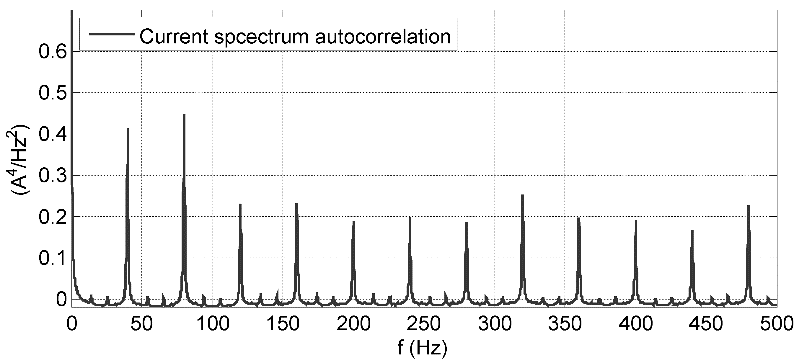
В предлагаемом методе, вместо использования лишь первого пика для определения дистанции между частотами, используется каждый пик сигнала автокорреляции. Это повышает точность определения. К тому же, точность определения зависит от разрешения спектра и это разрешение зависит от T_b. Если значение этого параметра мало, разрешение спектра будет плохим. Для того, чтобы избежать этой проблемы, используются несколько пиков для определения расстояния. Используемые пики – это пики между f_min и f_max. По этой причине расстояние между f_min и f_max должно быть достаточным, чтобы содержать все необходимые пики для улучшения вычисления расстояния между пиками. Чтобы уменьшить величину шума и определить пики, производимые скоростью двигателя, каждое значение сигнала автокорреляции сравнивается с уставкой A_min. Если текущее значение меньше, чем A_min, то оно приравнивается нулю, а если больше, то остаётся прежним:

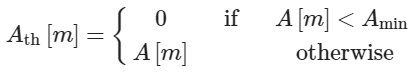(11)

где A_th – это обновленный сигнал.

Для определения пиков в автокорреляции, последний сигнал раскладывается следующим образом:

(12)

где D – это производная сигнала. Отсюда, пик присутствует, если производная отрицательная, а её предыдущее значение положительно:

(13)

где D_p – это сигнал, принимающий дискретные значения, которые показывают наличие пика.

Одного лишь этого метода определения пиков недостаточно; он определяет не только пики, производимые скоростью двигателя, но и небольшие нежелательные пики, возникающие из-за шума. По этой причине необходимо отсеять пики, производимые шумом. Чтобы это сделать, рассчитывается расстояние между пиками и затем рассчитывается параметр статистической моды этих расстояний. Рассчитанное расстояние – это дискретное измерение, которое измеряет количество замеров между пиками.

Статистическая мода используется для отсеивания пиков, производимых шумом. Каждое рассчитанное расстояние сравнивается с модой и, если абсолютная разница больше уставки d_a, это расстояние отсеивается и удаляется из последовательности.

Наконец, рассчитывается среднее расстояние из значений, которые не были отсеяны. Это значит, что расстояние умножается на разрешение спектра, R_spectrum:

(14)

Новое значение – это приближенное значение расстояния между частотами, которые содержатся в спектре тока.

3.3. Блок отслеживания частоты

Блок отслеживания частоты (рисунок 3) отслеживает пик в спектре тока и выдает частоту пика. Блок-схема отслеживания частоты изображена на рисунке 6. Эта схема имеет такой же вид, как и фазовая автоподстройка частоты (PLL). В ней содержится 4 элемента: управляемый источник напряжения (VCO), умножение (или определитель фазы), фильтр низких частот и сумматор. Эти четыре элемента являются типичными для схемы фазовой автоподстройки частоты (ФАПЧ) [32].

Рисунок 6 – Блок-схема отслеживания частоты. VCO: управляемый источник напряжения

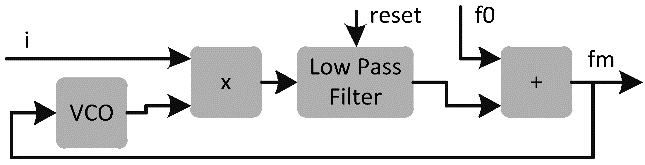
Блок отслеживания частоты имеет три входных сигнала: ток, i, центральную частоту, f₀, и сброс, reset; а также один выходной сигнал – частоту найденного пика, f_m.

Когда активен сигнал reset, блок отслеживания частоты отслеживает пик в спектре, ближайший к f₀, а когда сигнал reset неактивен, он отслеживает пик, ближайший к пику, найденному на предыдущей итерации.

В блоке отслеживания частоты, источник напряжения генерирует синусоидальный сигнал с частотой f_m, что является частотой пика, найденного на предыдущей итерации. Блок умножения перемножает ток на сигнал, сгенерированный источником. Фильтр низких частот получает постоянную составляющую сигнала и это значение зависит от частоты пика. Сумматор прибавляет f₀ к постоянной составляющей, полученной фильтром низких частот.

Предложенный и используемый в этой работе фильтр низких частот имеет следующую передаточную функцию:

(15)

где τ₁ и τ₂ – это постоянные времени фильтра, s – оператор Лапласа. Вторая часть этой передаточной функции может быть выполнена в цифровом виде. Для этой работы интегратор 1/s был выполнен по трапецеидальному правилу:

(16)

где v – это выход интегратора, u – это вход, n – это текущая дискрета (дискретное время), а dt – это период дискретности (значение, обратное частоте дискретности).

Когда сигнал reset активен, единственный затронутый элемент это фильтр низких частот, который сбрасывается в начальные условия. В предложенном фильтре это делается сбросом интегратора v[n] в ноль.

Этот фильтр приводит к ФАПЧ второго типа второго порядка. Из-за того, что блок отслеживания частоты схож с ФАПЧ, полный его анализ может быть найден в любом руководстве или книге о ФАПЧ [32].

3.4. Блок проверки

Блок проверки решает, будет ли выполнен блок определения df_m в следующей итерации и необходимо ли сбросить блок отслеживания частоты.

Блок проверки (рисунок 3) имеет два входных сигнала и три выходных. Входными являются выход блока определения df_m и выход блока отслеживания частоты, f_m. Выходной сигнал, ex_dfm, блока проверки показывает, будет ли блок определения df_m выполнен на следующей итерации. Выходной сигнал reset определяет, будет ли сброшен блок отслеживания частоты, если да, то выходной сигнал f₀ показывает новую центральную частоту блока отслеживания частоты.

ЭЧтобы получить эти выходные сигналы, блок проверки сравнивает частоту f_m, определенную блоком отслеживания частоты, с приближенным значением этой частоты. Это значение происходит из расстояния между частотами, df_m, и индекса компоненты тока, используемой для определения скорости, #f. Если разница между ними не слишком велика, тогда выходные сигналы ex_dfm и reset сохраняют свои значения. В ином случае, выходные сигналы изменяются на правильные значения. Чтобы уменьшить затраты вычислительной мощности, это сравнение происходит не на каждой итерации; вместо этого оно происходит каждые IM итераций.

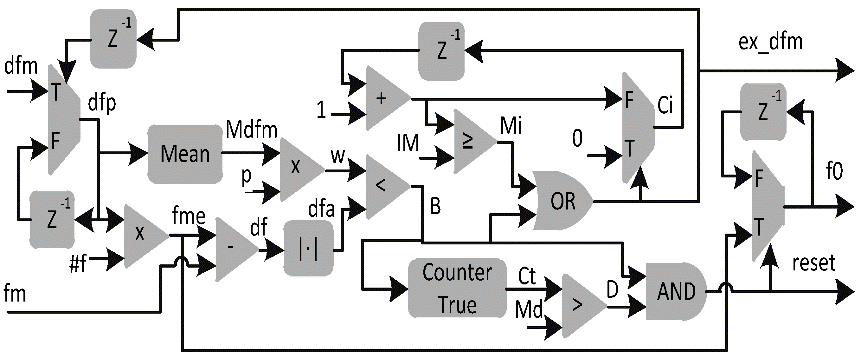
Блок-схема блока проверки показана на рисунке 7. Входными сигналами являются df_m и f_m, а выходными ex_dfm, f₀ и reset. Другие являются параметрами алгоритма. В схеме треугольные блоки выполняют такие арифметические операции, как вычитание или умножение. Эти треугольные блоки также включают элементы сравнения, такие как «больше» и «больше или равно». Когда эти блоки выполняют операции сравнения, выходом является бинарная величина, True(T) или False(F). Трапеции являются мультиплексорами и они управляются бинарным входом, который выбирает тот или другой вход в зависимости от значения выбранного входа. Блоки с символом Z^-1 это блоки задержки. Этот блок задерживает входное значение на одну итерацию. Блок среднего значения (Mean) вычисляет среднее значение последних L значений df_m согласно формуле:

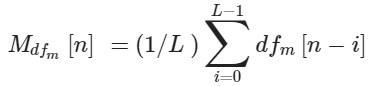(17)

Рисунок 7 – Блок-схема блока проверки

Блок Counter True считает сколько раз входной сигнал принимал значение True среди последних L значений. Если бинарное значение True заменить на 1, а False на 0, то выход этого блока можно рассчитать следующим образом:

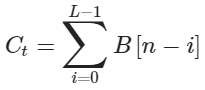(18)

Блоки AND и OR это блоки, которые выполняют логические операции И/ИЛИ. Блок с символом |⋅| вычисляет модуль входного сигнала.

Согласно рисунку 7, входной сигнал df_m используется только когда блок определения df_m был выполнен на текущей итерации, другими словами, когда выходной сигнал ex_dfm принимает бинарное значение True на предыдущей итерации. Когда блок определения df_m не выполняется, используется последнее значение, содержащееся в звене задержки. Когда df_p вычислено, тогда вычисляется среднее значение из последних L значений сигнала df_p и также определяется позиция f_m. Это значение, f_me, получается путём умножения df_p на #f. Параметр #f это позиция или индекс пика частоты, используемого для нахождения скорости. Значение f_me недостаточно точное, чтобы использовать его в вычислении скорости двигателя. Поэтому используется блок отслеживания частоты для повышения точности. Когда f_me вычислено, вычисляется расстояние между f_me и f_m, обозначенное df_a. Это делается блоком вычитания и блоком модуля. Максимальное допустимое расстояние между обеими частотами, w, получается путём вычисления среднего значения df_p из последний L значений и умножения этого среднего значения на параметр p, где p – это значение от 0 до 1. Когда df_a и w вычислены, обе величины сравниваются и вычисляется B. B – это бинарное значение, которое показывает, когда w меньше, чем df_a. B показывает, что расстояние между f_m и приближенным значением находится в допустимых пределах. B используется для вычисления C_t согласно уравнению (18). C_t определяет сколько раз допустимое расстояние между f_m и приближенным значением было превышено за последние L итераций. Далее, вычисляется D. D показывает больше ли C_t, чем максимальное допустимое количество превышений допустимой дистанции, M_d. Со значениями B и D вычисляется выходной сигнал reset, он равен True, когда обе величины, B и D. имеют значение True. Также, когда reset принимает значение True, выходной сигнал f₀ обновляется и принимает значение f_me. Если reset имеет значение False, остаётся значение прошлой итерации.

Выходной сигнал ex_dfm вычисляется по значениям B и M_i. Выход ex_dfm принимает значение True, когда одна или обе переменных равны True. M_i принимает значение True, когда значение счётчика C_i больше, чем максимум, IM. Счётчик C_i сбрасывается в 0, если ex_dfm принимает значение True и увеличивается, если ex_dfm принимает значение False. Выход ex_dfm принимает значение True в двух случаях: (1) когда расстояние между f_m и приближенным значением f_me больше, чем максимальное допустимое расстояние, w; (2) когда ex_dfm не принимал значение True в течение последних IM итераций.

3.5. Преобразователь

Блок преобразователя (рисунок 3) вычисляет скорость щеточного ДПТ, n, используя частоту f, полученную блоком отслеживания частоты. Обе величины связаны линейной функцией согласно уравнению (9). Из-за того, что блок отслеживания частоты отслеживает составляющую тока с индексом #f, отношение между f_m и n будет следующим:

(19)

где n – это скорость двигателя, f_m – это выход блока отслеживания частоты, #f – это индекс составляющей тока, используемой для нахождения скорости двигателя.

4. Экспериментальное подтверждение

Этот раздел описывает ход эксперимента для подтверждения описанного метода определения скорости двигателя.

4.1. Описание системы

Система, используемая для оценки точности предложенного метода, состояла из щеточного ДПТ, датчика тока, платы сбора данных и компьютера. На рисунке 8 изображена схема оборудования для эксперимента.

Рисунок 8 – Схема системы

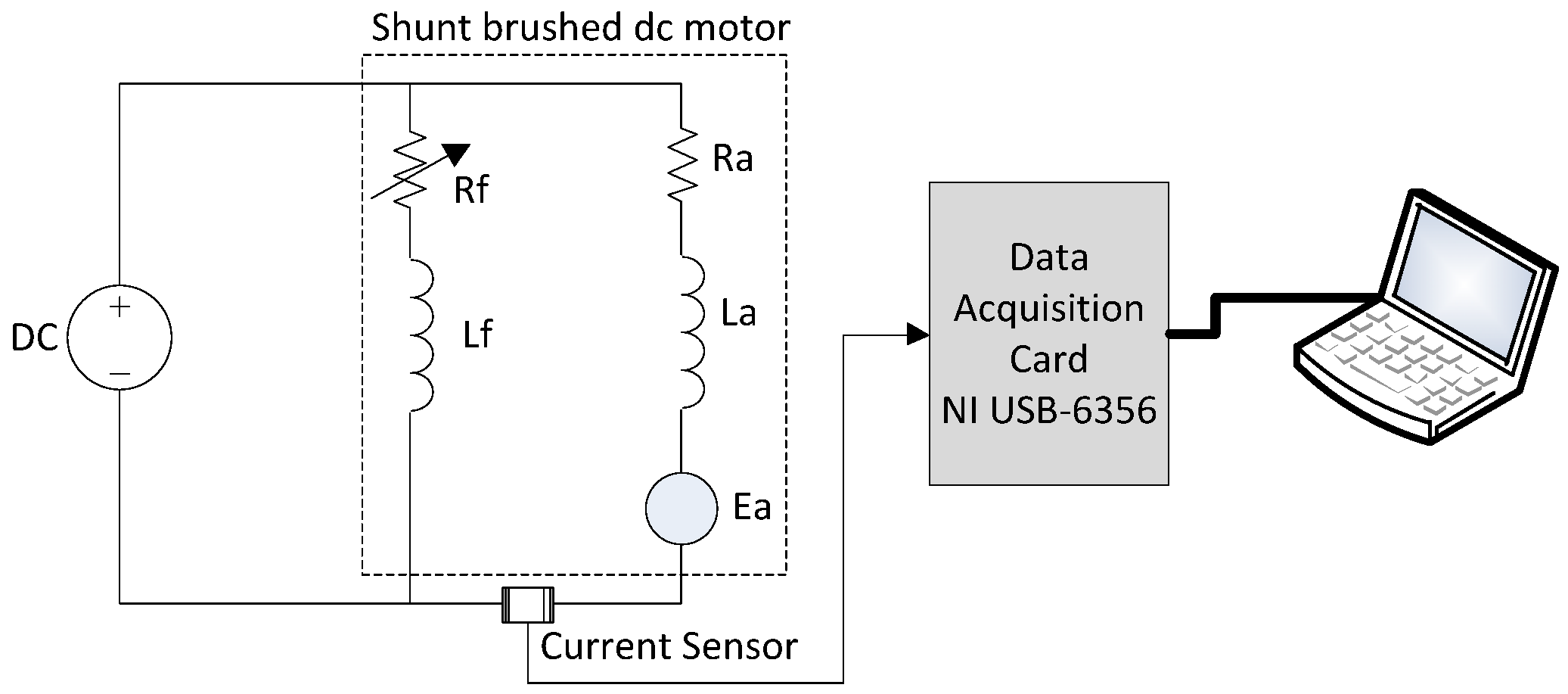
Для этого теста была использована универсальная электрическая машина, H-REM-120-CM Universal Laboratory Machine (ULM) от Hampden® Engineering Corporation (East Longmeadow, MA, США). Эта универсальная машина соединена с динамометром постоянного тока с оборотной рамой. Статор универсальной машины состоит из 24 ячеек с 12-оборотными витками. Ротор универсальной машины состоит из 36 ячеек, имеет два полюса, обмотку постоянного тока с полным шагом, состоящую из 72-оборотных витков, соединенные с 72 сегментами коллектора. Эта машина может быть соединена различными способами, что позволяет её использовать как однофазный асинхронный двигатель, трёхфазный асинхронный двигатель, синхронный двигатель и как двигатель постоянного тока с последовательным или параллельным возбуждением. Для этой работы машина была соединена в схему щеточного двигателя постоянного тока с параллельным возбуждением. В этой конфигурации получается двигатель мощностью 1 кВт при напряжении 100 В.

Использовался датчик тока AYA IBP 200:1 ((Pulse Electronics, San Diego, CA, США). Этот датчик имеет трансформатор тока (ТТ), соединённый к 2-Ω прецизионному резистору (Caddock, Roseburg, OR, США). Этот резистор позволяет преобразовать ток в сигнал напряжения, чтобы подключить его к системе сбора данных. Датчик тока был включен в цепь якоря возле щёток двигателя, как показано на рисунке 8. Следует отметить, что измерялся только ток якоря. Трансформатор тока был выбран намеренно, потому что он не трансформирует постоянный ток. Такой выбор позволяет получить более высокую точность при измерении переменной составляющей. В качестве платы сбора данных была выбрана NI USB-6356 от National Instruments (Austin, TX, США). Она имеет 8 одновременных аналоговых входов с частотой дискретности 1,25 миллионов выборок в секунду на канал, 2 аналоговых выхода с частотой 3,33 миллионов выборок в секунду и 24 цифровых входа-выхода. Один аналоговый вход был подключен к датчику тока. Плата сбора данных была подключена к компьютеру.

Использовался компьютер ASUS Notebook серии K72Jk (Taipei, Тайвань) с процессором Intel® Core™ i3 CPU M350 (Santa Clara, CA, США), 4 ГБ оперативной памяти и жестким диском объемом 500 ГБ. Использовалась операционная система Windows 7, а в качестве среды разработки использовалось программное обеспечение LabVIEW 2010 от National Instruments (Austin, TX, США). Компьютер был настроен на работу в системе мягкого реального времени, а плата сбора данных настроена на получение выборок в непрерывном режиме.

Не было необходимости в дополнительном измерении реальной скорости двигателя, чтобы оценить точность предлагаемого метода, потому что реальная скорость измерялась энкодером. Использовался энкодер Monarch Instrument ACT 3 Tachometer/Totalizer/Ratemeter (Amherst, NH, USA). Этот энкодер был настроен на выдачу аналогового сигнала напряжения, пропорционального скорости двигателя. Значение смещения и отмасштабированное значение скорости энкодера были запрограммированы на значения, близкие к рабочей скорости двигателя, чтобы достичь высокого разрешения измерения скорости. Этот энкодер и его соединения не включены в рисунок 8.

4.2. Сбор данных

Параметры двигателя отслеживались при различных условиях, чтобы оценить точность предлагаемого метода. Как было описано ранее, измерения включали в себя ток якоря и реальную скорость двигателя. Частота дискретности составляла 100 000 выборок в секунду (на канал) в непрерывном режиме, время T_b составляло одну секунду, а используемый диапазон был ограничен на f_min = 1000 Гц и f_max = 5000 Гц.

Были проведены три теста: на постоянной скорости, с медленно изменяющейся скоростью и с быстро изменяющейся скоростью. Первый тест включал в себя 12 разных фиксированных скоростей между 2000 и 3000 об/мин. Такой скоростной диапазон был выбран потому, что это рабочий диапазон тестируемого двигателя. Второй тест заключался в медленном изменении скорости от 2000 об/мин до 2900 об/мин. Изменения скорости двигателя производились путём изменения нагрузки двигателя и/или тока возбуждения.

Для этих трёх тестов были вычислены средняя ошибка и стандартное отклонение, обе в абсолютных значениях (об/мин) и в относительных (%).

4.3. Сравнение вычислений с измерениями

Результаты первого теста, теста с постоянной скоростью, представлены в таблице 1. Эта таблица содержит скорость двигателя, измеренную тахометром, а также ошибки в вычислении скорости для двенадцати тестовых скоростей. Среднее значение ошибки и стандартное отклонение составили менее 1 об/мин, а их относительные значения составили менее 0,01%.

Таблица 1 – Значения ошибок при измерении скорости

Результаты второго теста, теста с медленно изменяющейся скоростью, показаны на рисунке 9. Этот рисунок показывает реальную скорость в сравнении с её вычисленным значением и ошибку при её вычислении. Средняя ошибка во время этого теста составила 0,2863 об/мин, а стандартное отклонение составило 1,267 об/мин.

Рисунок 9 – Реальная и вычисленная скорости при медленном её изменении

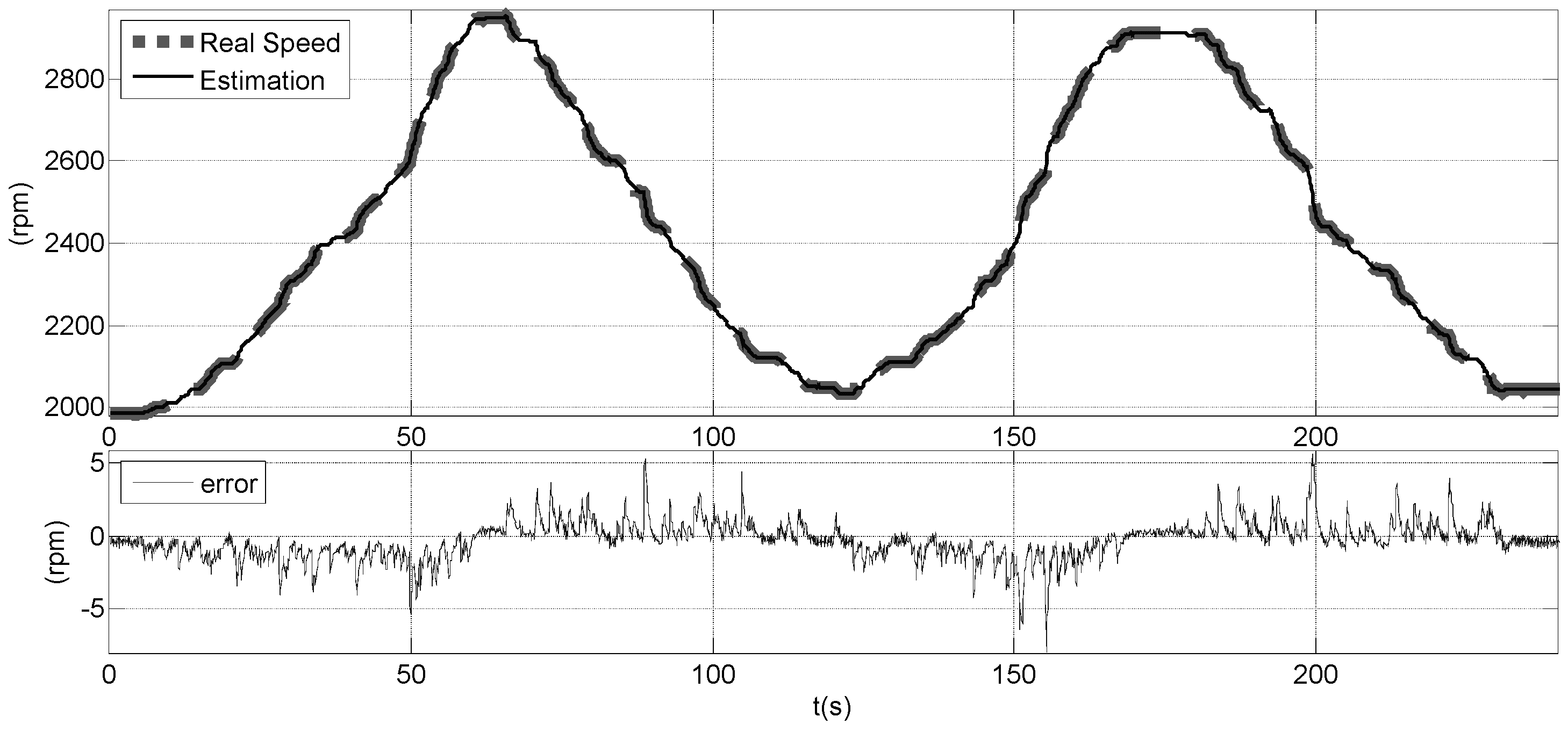
Результаты третьего теста, теста с быстро изменяющейся скоростью, показаны на рисунке 10. На этом рисунке изображена реальная скорость в сравнении с её вычисленным значением и ошибка при её вычислении. Средняя ошибка во время этого теста составила 0,6658 об/мин, а стандартное отклонение составило 1,1484 об/мин.

Рисунок 10 – Реальная и вычисленная скорости при быстром её изменении

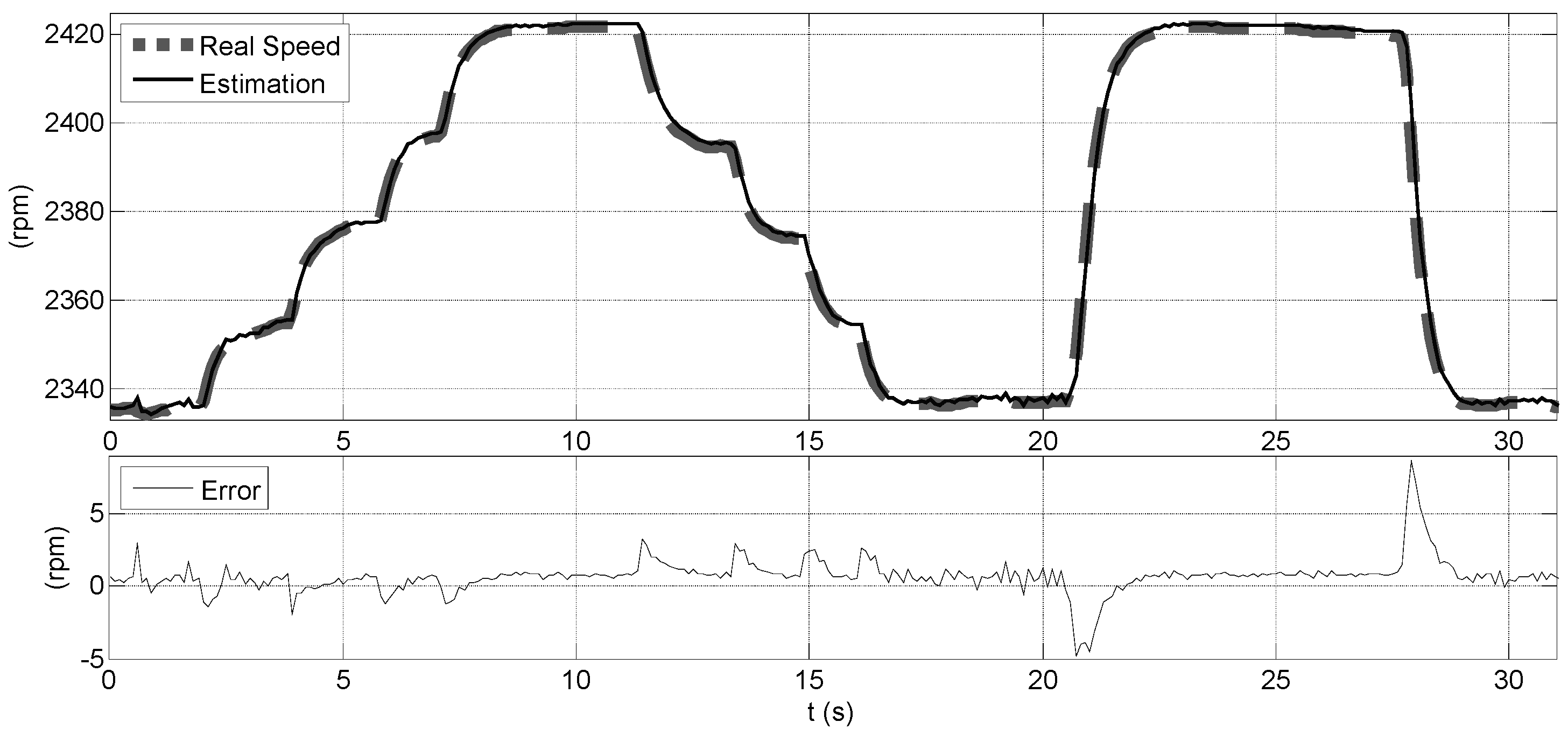
Три теста, при постоянной скорости, при медленно изменяющейся скорости и при быстро изменяющейся скорости, проведённые в диапазоне скоростей от 2000 до 3000 об/мин, показали, что среднее значение ошибки составило менее 1 об/мин, а стандартное отклонение менее 1,5 об/мин. Эти результаты показывают, что предложенный метод работает корректно при постоянной, при медленно изменяющейся и при быстро изменяющейся скоростях.

5. Выводы

Настоящая статья представила новый бездатчиковый метод определения скорости щеточного двигателя постоянного тока с большим числом витков, как интегральный ДПТ. Этот метод обладает следующими особенностями:

1. Это новый метод, который не может быть включен ни в одну категорию бездатчиковых методов; его нельзя отнести ни к группе методов, основанных на динамической модели, ни к группе методов, основанных на пульсирующей составляющей. Он принадлежит к новой группе бездатчиковых методов, которая изучает спектральные составляющие тока и имеет преимущества обоих предыдущих групп.
2. Он требует лишь измерения тока ДПТ для вычисления скорости. Остальные методы, напротив, требуют измерения и тока, и напряжения для ДПТ с большим количеством витков.
3. Он может быть использован для щеточных ДПТ с большим числом витков, таких как интегральные ДПТ мощностью 1 л.с. Другие методы, основанные на пульсирующей составляющей, которые измеряют только ток, наоборот, могут быть использованы лишь для ДПТ с малым количеством витков, где пульсирующая составляющая достаточно велика.
4. Он обладает малой погрешностью при вычислении скорости в проведенных тестах. Среднее значение ошибки при использовании этого метода составляет менее 1 об/мин, а стандартное отклонение менее 1,5 об/мин для скоростей от 2000 до 3000 об/мин для двигателя H-REM-120-CM, настроенного как щеточный ДПТ с параллельным возбуждением.

Комментарии автора

Настоящая статья была выполнена в три этапа. Первый этап заключался в формулировке цели работы и содержания статьи, второй этап заключался в сборе и обработке данных. Оба этих этапа были выполнены Ernesto Vazquez-Sanchez и Joseph Sottile в Lexington, США, при прохождении докторантуры во время кратковременной стажировки, проводимой Ernesto Vazquez-Sanchez в университете Kentucky. Третий этап, который заключался в написании статьи, был выполнен совместно тремя авторами, пока Ernesto Vazquez-Sanchez и Jaime Gomez-Gil находились в университете Valladolid, Испания, а Joseph Sottile находился в университете Kentucky, США.

Конфликт интересов

Авторы объявили, что нет никаких конфликтов интересов.

Список использованной литературы

1. Sul, S. Control of Electric Machine Drive System, 1st ed.; Wiley-IEEE Press: Piscataway, NJ, USA, 2011. [Google Scholar]
2. Hilairet, M.; Auger, F. Speed sensorless control of a DC-motor via adaptive filters. IET Electr. Power Appl. 2007, 1, 601–610. [Google Scholar] [CrossRef]
3. Chevrel, P.; Siala, S. Robust DC-motor speed control without any mechanical sensor. In Proceedings of the IEEE International Conference on Control Applications, Hartford, CT, USA, 5–7 October 1997; pp. 244–246.
4. Yachiangkam, S.; Prapanavarat, C.; Yungyuen, U.; Po-ngam, S. Speed-sensorless separately excited DC Motor drive with an adaptive observer. In Proceedings of the IEEE Technical Conference on Computers, Communications, Control and Power Engineering (TENCON 2004), Chiang Mai, Thailand, 21–24 November 2004; Volume D, pp. 163–166.
5. Kowal, D.; Patan, M.; Paszke, W.; Romanek, A. Sequential design for model calibration in iterative learning control of DC motor. In Proceedings of the 20th International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzydroje, Poland, 24–27 August 2015; pp. 794–799.
6. Lobosco, O.S. Modeling and simulation of DC motors in dynamic conditions allowing for the armature reaction. IEEE Trans. Energy Convers. 1999, 14, 1288–1293. [Google Scholar] [CrossRef]
7. Bowes, S.R.; Sevinc, A.; Holliday, D. New natural observer applied to speed-sensorless DC servo and induction motors. IEEE Trans. Ind. Electron. 2004, 51, 1025–1032. [Google Scholar] [CrossRef]
8. Cupertino, F.; Pellegrino, G.; Giangrande, P.; Salvatore, L. Sensorless Position Control of Permanent-Magnet Motors With Pulsating Current Injection and Compensation of Motor End Effects. IEEE Trans. Ind. Appl. 2011, 47, 1371–1379. [Google Scholar] [CrossRef]
9. Kiyoshi, O.; Yoshihiro, N.; Yoshihisa, H.; Hirokazu, K. High-performance speed control based on an instantaneous speed observer considering the characteristics of a dc chopper in a low speed range. Electr. Eng. Jpn. 2000, 130, 77–87. [Google Scholar]
10. Castaneda, C.E.; Loukianov, A.G.; Sanchez, E.N.; Castillo-Toledo, B. Discrete-time neural sliding-mode block control for a DC Motor with controlled flux. IEEE Trans. Ind. Electron. 2012, 59, 1194–1207. [Google Scholar] [CrossRef]
11. Liu, Z.Z.; Luo, F.L.; Rashid, M.H. Speed nonlinear control of DC motor drive with field weakening. IEEE Trans. Ind. Appl. 2003, 39, 417–423. [Google Scholar]
12. Scott, J.; McLeish, J.; Round, W.H. Speed control with low armature loss for very small sensorless brushed dc motors. IEEE Trans. Ind. Electron. 2009, 56, 1223–1229. [Google Scholar] [CrossRef]
13. Farkas, F.; Halasz, S.; Kadar, I. Speed Sensorless Neuro-Fuzzy Controller for Brush type DC Machines. In Proceedings of the 5th International Symposium of Hungarian Researchers on Computational Intelligence, Budapest, Hungray, 11–12 November 2004; pp. 147–158.
14. Weerasooriya, S.; El-Sharkawi, M.A. Identification and control of a DC motor using back-propagation neural networks. IEEE Trans. Energy Convers. 1991, 6, 663–669. [Google Scholar] [CrossRef]
15. Aydogmus, O.; Talu, M.F. Comparison of Extended-Kalman- and Particle-Filter-Based Sensorless Speed Control. IEEE Trans. Instrum. Meas. 2012, 61, 402–410. [Google Scholar] [CrossRef]
16. Razi, R.; Monfared, M. Simple control scheme for single-phase uninterruptible power supply inverters with Kalman filter-based estimation of the output voltage. IET Power Electron. 2015, 8, 1817–1824. [Google Scholar] [CrossRef]
17. Radcliffe, P.; Kumar, D. Sensorless speed measurement for brushed DC motors. IET Power Electron. 2015, 8, 2223–2228. [Google Scholar] [CrossRef]
18. Afjei, E.; Ghomsheh, A.N.; Karami, A. Sensorless speed/position control of brushed DC motor. In Proceedings of the International Aegean Conference on Electrical Machines and Power Electronics (ACEMP’07), Bodrum, Turkey, 10–12 September 2007; pp. 730–732.
19. Sincero, G.C.R.; Cros, J.; Viarouge, P. Arc Models for Simulation of Brush Motor Commutations. IEEE Trans. Magn. 2008, 44, 1518–1521. [Google Scholar] [CrossRef]
20. Figarella, T.; Jansen, M.H. Brush wear detection by continuous wavelet transform. Mech. Syst. Signal Process. 2007, 21, 1212–1222. [Google Scholar] [CrossRef]
21. Yuan, B.; Hu, Z.; Zhou, Z. Expression of sensorless speed estimation in direct current motor with simplex lap winding. In Proceedings of the IEEE International Conference on Mechatronics and Automation, (ICMA 2007), Harbin, China, 5–8 August 2007; pp. 816–821.
22. Lott, J.; Burke, D. Brushed Motor Position Control Based Upon Back Current Detection. U.S. Patent 20060261763 A1, 23 November 2006. [Google Scholar]
23. Won-Sang, R.; Hye-Jin, L.; Jin Bae, P.; Tae-Sung, Y. Practical Pinch Detection Algorithm for Smart Automotive Power Window Control Systems. IEEE Trans. Ind. Electr. 2008, 55, 1376–1384. [Google Scholar]
24. Micke, M.; Sievert, H.; Hachtel, J.; Hertlein, G. Method and Device for Measuring the Rotational Speed of a Pulse-Activated Electric Motor Based on a Frequency of Current Ripples. U.S. Patent 7265538 B2, 4 September 2007. [Google Scholar]
25. Vazquez-Sanchez, E.; Gomez-Gil, J.; Rodriguez-Alvarez, M. Analysis of three methods for sensorless speed detection in DC motors. In Proceedings of the IEEE International Conference on Power Engineering, Energy and Electrical Drives (POWERENG ‘09), 18–20 March 2009; pp. 117–122.
26. Kessler, E.; Schulter, W. Method for Establishing the Rotational Speed of Mechanically Commutated DC Motors. U.S. Patent 6144179 A, 7 November 2000. [Google Scholar]
27. Vazquez-Sanchez, E.; Gomez-Gil, J.; Gamazo-Real, J.C.; Diez-Higuera, J.F. A new method for sensorless estimation of the speed and position in brushed dc motors using support vector machines. IEEE Trans. Ind. Electron. 2012, 59, 1397–1408. [Google Scholar] [CrossRef]
28. Moller, D.D.; Schneider, P.K.; Canales, S.A. Voltage-Sensitive Oscillator Frequency for Rotor Position Detection Scheme. U.S. Patent 7352145 B2, 1 April 2008. [Google Scholar]
29. Toliyat, H.A.; Kliman, G.B. Handbook of Electric Motors; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
30. Chiasson, J. Modeling and High Performance Control of Electric Machines, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2005. [Google Scholar]
31. Yarlagadda, R.K.R. Analog and Digital Signals and Systems, 1st ed.; Springer Publishing Company, Incorporated: Stillwater, OK, USA, 2009. [Google Scholar]
32. Egan, W. Phase-Lock Basics, 2nd ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2007. [Google Scholar]