Проектирование ПИД-регулятора для системы управления скоростью двигателя постоянного тока с нелинейностями
Авторы: А.И. Бобиков, А.О. Бозванов
Источник: Рязанский государственный университет имени С.А. Есенина – Информатика и прикладная математика: Межвузовский сборник научных трудов (22), 2016, с. 21-24
Аннотация
Увеличивающийся спрос на использование двигателей постоянного тока для различных промышленных применений за последние несколько десятилетий сделали их одним из самых важных системных приводов. Нелинейные параметры, такие как зона нечувствительности, насыщение и люфт, вызывают наибольшую тревогу при управлении скоростью двигателя постоянного тока. Чтобы уменьшить влияние этих нелинейностей и для того чтобы улучшить эффективность системы в статье предлагается использовать ПИД-регулятор настроенный с помощью пакета Simulink Response Optimization среды MATLAB. Целью работы является проектирование ПИД-регулятора, который будет способен устранить или ослабить влияние нелинейностей на скорость двигателя постоянного тока. В статье рассмотрена система управления скоростью двигателя постоянного тока, построенная с использованием инструмента Simulink в пакете приложений MATLAB.
Ключевые слова: двигатель постоянного тока, нелинейности, ПИД-регулятор, градиентный метод.
Введение.
Двигатели постоянного тока (ДПТ) используются для обеспечения вращательного или прямолинейного движения в различных электромеханических устройствах [1]. Они находят свое применение во многих отраслях производства. Однако, несмотря на интенсивные исследования всё ещё ДПТ до сих пор обладают нелинейными свойствами и имеют параметры, влияющие на их качество и требующие разработки более сложных СУ.
Первым важным нелинейным свойством ДПТ является зона нечувствительности, которое замедляет реакцию системы и требует большего сигнала управления для достижения желаемой скорости. Второе важное нелинейное свойство ДТП–эффект насыщения, при котором выходной сигнал двигателя не может достигнуть требуемого значения. Математическим описанием третьего нелинейного эффекта, имеющего место в ДПТ, является воздушный зазор (люфт) в редукторах двигателя.
В статье [2] для настройки параметров ПИД-регулятора используется метод Циглера- Николса, который представляет собой набор правил для определения значений пропорционального коэффициента усиления, времени интегрирования и времени дифференцирования, на основе переходных характеристик реакции системы управления. Регуляторы, параметры которых рассчитаны по методу Циглера-Николса, не всегда обеспечивают требуемое качество процесса регулирования. Как правило, требуется ручная подстройка их параметров.
Для оптимизации настройки параметров ПИД-регулятора в статье предлагается метод с использованием пакета Simulink Response Optimization среды MATLAB. С помощью данного пакета можно найти оптимальные параметры настройки регулятора, которые обеспечивают требуемый переходной процесс по заданным графическим ограничениям во временной области.
Пакет Simulink Response Optimization.
Пакет Simulink Response Optimization представляет графический интерфейс пользователя для осуществления проектирования СУ во временной области. С помощью пакета Simulink Response Optimization можно найти оптимальные параметры настройки для нелинейной модели системы в SIMULINK, которые обеспечат требуемый переходной процесс по заданным графически ограничениям в окне временной области. Любое число переменных SIMULINK, включая скалярные, векторные и матричные величины, могут быть объявлены настраиваемыми или оптимизируемыми. Для этого надо ввести имена переменных в соответствующем диалоговом боксе. Границы неопределенности можно задать для любых переменных модели СУ [3].
Пакет Simulink Response Optimization автоматически преобразует ограничения во временной области в ограничения задачи оптимизации параметров СУ и затем решает задачу, используя алгоритмы и процедуры, заложенные в пакете. Ход процесса оптимизации можно видеть в графическом окне задания ограничений прямо при выполнении симуляции. По окончанию процесса оптимизации результаты можно просмотреть в рабочем окне MATLAB. Промежуточные результаты выводятся там после каждого шага симуляции. Оптимизацию параметров можно прервать до ее окончания с целью вывода промежуточных результатов или изменения модели.
Теоретические сведения о ДПТ.
Двигатель постоянного тока имеет два основных компонента. Первый – электрический компонент, состоящий из сопротивления R, индуктивности L, входного напряжения V и противоэлектродвижущей силы E. Второй – механический компонент, благодаря которому создается полезное механическое вращательное движение на валу. А именно – вал привода, момент инерции привода и инерции нагрузки J, и затухание b.
На рис. 1 изображена типичная модель ДПТ. Через ω обозначена угловая скорость вала.
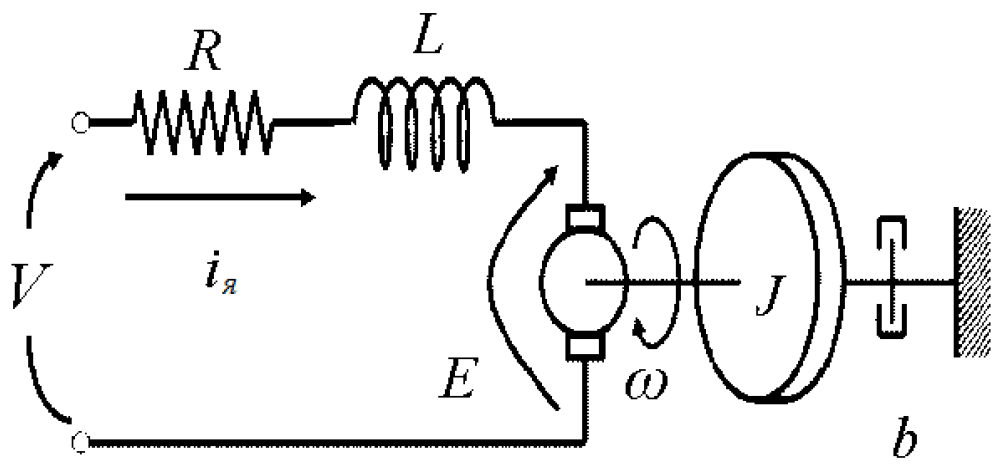
Построение модели ДПТ.
С помощью законов Ньютона и Кирхгофа и рис. 1 получаем передаточную функцию, связывающую входное напряжение V и угловую скорость двигателя ω:
| (1) |
где R – сопротивление, L – индуктивность, J – момент инерции привода и нагрузки, b – вязкое трение, k – конструктивный параметр.
С использованием передаточной функции ДПТ (1) была построена модель ДПТ в Simulink (рис. 2). Также в нее были добавлены нелинейности, присущие двигателю постоянного тока.
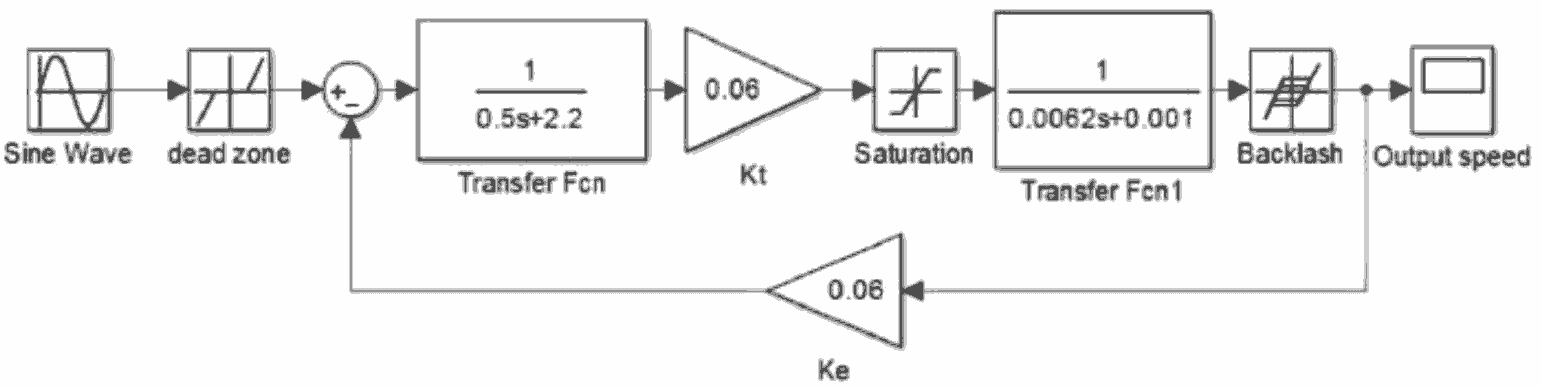
Разработка оптимального ПИД-регулятора.
Задача оптимизации параметров ПИД-регулятора с учетом наложенных ограничений, сформулированная в пакете Simulink Response Optimization [3], последовательно вызывает симуляцию работы модели СУ в Simulink, сравнивает полученные результаты с заданными ограничениями переходного процесса и, используя градиентный метод, изменяет настраиваемые параметры для достижения заданной формы процесса. Схема с обратной связью для модели ДПТ представлена на рис. 3.
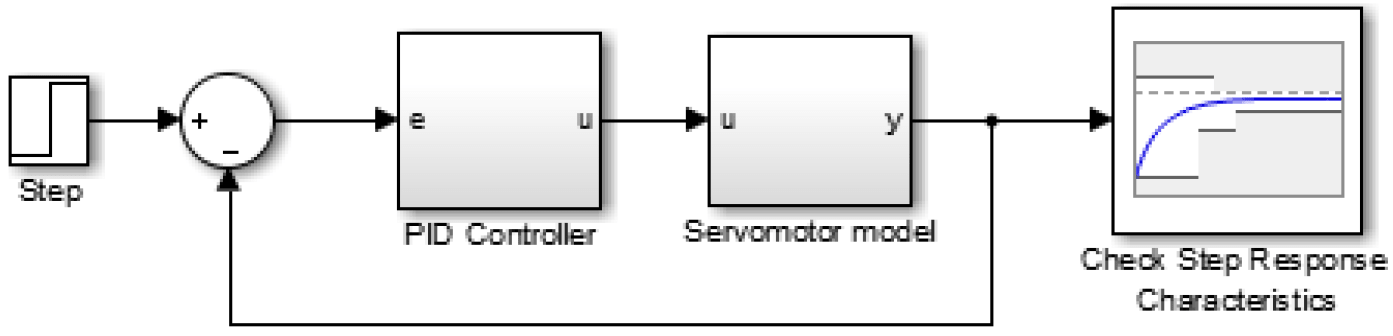
Для сравнение методов, предложенных в данной статье, был использован ступенчатый входной сигнал с максимальным значением, равным 12 вольт, что является максимальным напряжением для используемого ДПТ. Полученные результаты представлены в таблице 1.
Таблица 1
|
Метод Циглера-Николса |
Simulink Response Optimization |
σ, % |
20,41 |
6,42 |
tp, с |
8,58 |
6,33 |
Как видно по характеристикам переходного процесса ПИД-регулятор, настроенный с помощью Simulink Response Optimization имеет меньшую величину перерегулирования и времени регулирования, что повышает качество переходного процесса.
Основным достоинством данного метода перед методом Циглера-Николса заключается в том, что процесс настройки ПИД-регулятора происходит автоматически, что дает оптимальные параметры и повышает точность воспроизведения задающего воздействия СУ ДПТ.
Заключение.
В данной статье разработан ПИД-регулятор настроенный с помощью пакета Simulink Response Optimization, который ослабляет влияние нелинейностей на скорость двигателя постоянного тока и повышает качество переходного процесса, а именно: уменьшает величину перерегулирования и времени регулирования.
Библиографический список литературы
- Гусев Н.В. Алгоритмическое обеспечение систем управления следящими электроприводами // Научно-технический и учебно-образовательный журнал: Известия высших учебных заведений. Электромеханика. – 2006. № 3. – C. 57-60.
- Бобиков А.И., Сурков И.И. Нейросетевое управление скоростью двигателя постоянного тока // Вестник РГРТУ. № 2 (выпуск 52). Рязань, 2015.
- Дьяконов В. П. Simulink 5/6/7: самоучитель //ДМК Пресс, Москва, 2006. – 784с.