НАХОЖДЕНИЕ ОБЛАСТИ УСТОЙЧИВОГО ПРОЦЕССА ШЛИФОВАНИЯ С УЧЕТОМ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ СТАНКА

Аннотация

Чернорай А. А., Полтавец В. В. Нахождение области устойчивого процесса шлифования с учетом динамических характеристик элементов станка В статье рассмотрено определение области устойчивого процесса шлифования с использованием частотного критерия устойчивости, описано построение АФЧХ станка и граничных кривых

Введение

Получение поверхностей изделий требуемого качества при абразивной обработке зависит, как правило, от обеспечения оптимального сочетания динамического состояния станка с технологическими факторами. Проявляющаяся зачастую при обработке нестабильность процесса резания приводит к ухудшению показателей качества обработки вследствие возбуждения в зоне резания колебаний недопустимо высокого уровня. С целью уменьшения вероятности формирования детерминированной вибрации на частотах собственных и вынужденных колебаний обычно используют ограничение режимов резания, что нежелательно отражается на производительности процесса. Улучшение динамических показателей станка чаще всего обеспечивает смещение допустимой границы режимов в сторону их увеличения. Отсюда следует вывод о потенциальной возможности повышения качества обработки путем улучшения динамического состояния станка.

Однако стремление проектировать наиболее ответственные узлы металлообрабатывающего оборудования с улучшенными динамическими характеристиками не всегда приводят к желаемому результату. Это связано со способностью формообразующих подсистем станка образовывать при резании отличающиеся от ожидаемых динамические свойства [1].

Целью работы является рассмотрение метода исследования виброустойчивости шлифовальных станков с помощью частного критерия устойчивости.

Основное содержание работы

Основные особенности динамической системы металлорежущего станка заключаются в ее замкнутости и многоконтурности, рабочие процессы взаимосвязаны друг с другом через упругую систему, причем обратным влиянием упругой системы на рабочие процессы, как правило, пренебречь нельзя. Однако, в отдельных случаях, учитывая только наиболее существенные обратные связи, можно перейти к представлению об эквивалентной динамической системе станка как об одноконтурной системе (рис. 1) [2].

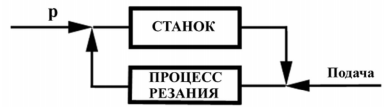
Рисунок 1. Представление станка и процесса резания как замкнутого контура [2]

Свойства элемента контура можно определить, если известны параметры его динамических характеристик. Для шпиндельного устройства шлифовальных станков это коэффициенты матриц А, В, С , где А – коэффициент квазиупругой системы, В – коэффициент диссипативной системы, С – коэффициент инерционной системы [2].

В работе [2] был предложен метод исследования виброустойчивости станков с помощью частотного критерия устойчивости. Данный метод основан на определении АФЧХ шпиндельного узла станка. Оценка виброустойчивости станка осуществляется путем построения областей устойчивости. Для этого определяется зависимость средней ширины стружки B_с или глубины шлифования t, снимаемой в процессе шлифования без вибраций, от скорости резания v_к. Также в работе [2] представлен алгоритм построения АФЧХ, который основан на алгоритме вычисления свободных колебаний. Элементы упругой системы, колебания которых занимают наиболее существенную долю в относительных колебаниях на той или иной частоте, выявляются путем построения форм колебаний на основании данных о величине абсолютных смещений элементов станка в определенный момент времени его работы.

Для построения АФЧХ относительных колебаний (рис. 2) на примере станка модели 3Г71М были рассчитаны, определены экспериментально и впоследствии сравнены динамические характеристики станка с целью выявления зоны, в которой обработка будет вестись наилучшим образом. При построении АФЧХ относительных колебаний были рассчитаны относительные колебания станка при силовых возмущениях от электродвигателя привода круга, при колебаниях фундамента и от действия дисбаланса шлифовального круга.

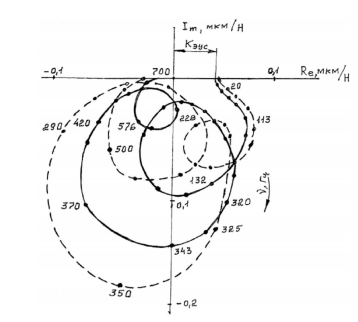
Рисунок 2. АФЧХ эквивалентной динамической системы станка 3Г71М сплошная линия – расчетные данные, штриховая – экспериментальные данные [2]

Расчет показал, что основная доля статической податливости станка модели 3Г71М приходится на шпиндель (44 %), подшипники шпинделя (21 %), консоль шпиндельной бабки (14 %) и механизм вертикальной подачи (15 %) [2]

Для построения граничной кривой в плоскости параметров глубины шлифования t или средней ширины срезаемой стружки B_с и скорости резания v_к (рис. 3) в работе [2] использовали известный из теории регулирования метод Д-разбиения. Таким путем определили границу областей устойчивости системы для обеспечения некоторого удаления режимных параметров от этой границы [3, 4]. Полученные кривые I и II (см. рис. 3) являются границей области устойчивого шлифования.

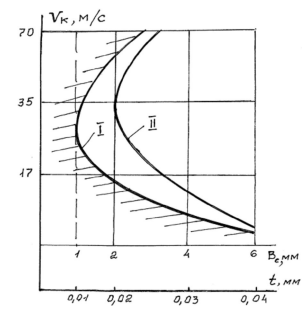
Рисунок 3. Кривая границ устойчивого шлифования: I – для станка 3Г71М, II – для станка 3Е711ИВ [2]

Выводы

В статье рассмотрен метод определения областей устойчивости при шлифовании, основанный на расчете свободных колебаний упругой системы станка. Преимуществом этого метода является то, что с его помощью можно как на этапе проектирования станка, так и при расчетах режимов резания прогнозировать и определять наиболее благоприятную зону для обработки.

Список литературы:

1. Бржозовский, Б.М. Обеспечение качества обработки шлифованием на основе синтеза оптимальных динамических свойств станка / Б.М. Бржозовский, М.Б. Бровкова, И.Н. Янкин // Известия Волгоградского государственного технического ун-та. &ndas; 2006. – № 2. – С. 20-22.
2. Зубарев, Ю.М. Расчет области устойчивого процесса шлифования с учетом динамических характеристик шпиндельных устройств / Ю.М. Зубарев, М.А. Алейникова // Инструмент и технологии. – 2005. – № 21-22. – С. 63-67.
3. Эльясберг, М.Е. Автоколебания металлорежущих станков: теория и практика / М.Е. Эльясберг. – СПб.: ОКБС, 1993. – 181 с.
4. Зубарев, Ю.М. Расчет шпиндельных устройств станка на устойчивость резания / Ю.М. Зубарев, Н.Н. Агаркова, М.А. Сикалова // Физические процессы при резании металлов: Сб. науч. работ. Волгоград-Ижевск. – Волгоград: ВолгГТУ, 1997. – С. 114-119.