МОДЕЛИРОВАНИЕ И ИМИТАЦИЯ ПРОЦЕССА: ВЗАИМОДЕЙСТВИЯ В СТАНКЕ ПРИ ШЛИФОВАНИИ

Модели процессов

Модель процесса шлифования описывает сложную взаимосвязь между процессом и параметрами станка, и результатами работы. Взаимодействие моделируется путем прогнозирования шлифовальных сил, температуры, энергии шлифования, целостности поверхности и т.д., в зависимости от процесса. Несколько подходов к построению модели процесса представлены в [1]. К ним относятся фундаментальные подходы, а также кинематические модели, метод конечных элементов (FEM), молекулярная динамика, физические и эмпирические, искусственные нейронные сети и модели, и основанные на правилах модели.

В этой главе основное внимание уделяется прогнозированию технологических процессов, возникающих во время шлифования, в качестве входного значения для модели станка, чтобы описать взаимодействие между процессом и структурой станка. Из-за большого количества абразивных зерен с неизвестной геометрией, которая изменяется со временем, шлифование представляет собой сложную операцию удаления материала [3].

Большое количество входных переменных усложняет разработку универсальной модели [4]. Из-за различных условий контакта было разработано несколько моделей, учитывающих различные операции шлифования.

Кинематико-геометрическое моделирование является основой представленных моделей процессов. Поэтому рассматривается проникновение между шлифовальным кругом и заготовкой. Кроме того, эти симуляции можно различать между микроскопическими и макроскопическими подходами, которые описаны ниже. Их сложность и точность зависят от выбранного подхода к моделированию и кинематики процесса шлифования [1].

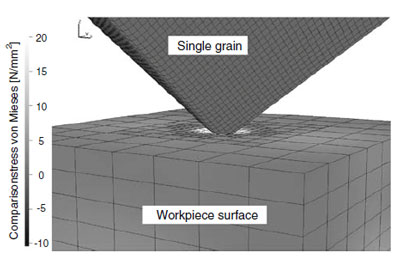
Рис. 1 Напряжение на поверхности детали, моделируемое FEM [5]

Микроскопические подходы

В микроскопических подходах подробно описаны компоненты, участвующие в механической обработке материала. В одном подходе шлифовальный круг состоит из подробного описания сложной трехмерной формы каждого отдельного зерна и его случайно распределенного положения и ориентации на колесе на основе статистических функций, определяемых подробным статистическим анализом топографий шлифовальных кругов [2]. Другие подходы измеряют топографию колеса и используют эти данные для детального моделирования.

Другой микроскопический подход показан на рисунке 1. Используется трехмерная имитационная модель FEM, показывающая возникающие напряжения при прохождении одного зерна. Моделирование может быть расширено за счет рассмотрения множества статистически распределенных зерен для представления зерен по определенным путям. Расчетные напряжения зерен используются для расчета сил процесса.

Основываясь на знании топографии шлифовального круга в сочетании с кинематикой процесса, можно моделировать обработанный материал каждым зерном с помощью 3D FEM.

Другой подход представлен на рисунке 2a. Он показывает идеальное проникновение отдельных зерен и поверхности заготовки на основе кинематики процесса и предположения об идеальном образовании стружки. Возможные параметры для характеристики недеформированных микросхем одиночного проникновения зерна показаны на рисунке 2b. Одиночные зерна моделируются идеальными октаэдрами, кубоидами, тетраэдрами и эллипсоидами, рандомизированными дополнительными плоскостями в разных ориентациях для создания сложной формы [6].

Знание обработанного материала и накопленных поперечных сечений стружки приводит к вычислению возникающих сил с использованием уравнения Киенцле [7], которое адаптировано для процессов шлифования. Из-за постоянно меняющихся условий контакта, особенно при шлифовании и шлифовании инструмента с ЧПУ, можно включить распределение эффективной силы шлифования.

Некоторые экспериментально определенные и смоделированные силы с соответствующими результирующими поверхностями показаны на рисунке 3. Экспериментально определенная специфическая для процесса шлифовальная сила k_c,sim связывает поперечное сечение чипа с силами измельчения. Моделирование приводит к хорошему приближению возникающих сил. Принимая во внимание различные топологии шлифовальных кругов, то есть распределение зерна и размер зерна, может быть достигнуто предсказание поверхности заготовки.

Макроскопические подходы

Макроскопические подходы описывают проникновение заготовки по форме шлифовального круга без подробных характеристик топографии колеса. На рисунке 4 показан 2D-подход для расчета обработанного материала с использованием продольной секции стружки в зависимости от глубины резания, скорости заготовки, выбранной временной ступени и положения шлифовального круга. Таким образом, учитывается обрабатываемый в настоящее время материал, который важен для процессов с быстро изменяющимися силами измельчения, например. во время фазы обкатки или заканчивания в маятниковом и скоростном шлифовании.

На основе модели эмпирического шлифования сила процесса также может быть определена с использованием трехмерного кинематико-геометрического моделирования [10]. Адаптированное уравнение Киенсло связывает обработанный материал с возникающими силами. Следовательно, необходим коэффициент для удельного отношения шлифовальной силы, который должен быть оценен с помощью эмпирических данных. Эмпирические данные генерируются экспериментами, учитывающими свойства материала и трибологические эффекты. В кинематико-геометрическом моделировании поверхности заготовки могут быть описаны с помощью моделей dexel. Модель dexel применяется в процессе шлифования NC-формы в [11, 12]. Таким образом, локальное распределение контактных напряжений может быть рассчитано с помощью макроскопического моделирования FEM.