Оценка напряженно-деформированного состояния рельсов при изготовлении

Авторы: В.В. Муравьев; К.А. Тапков

Приборы и методы измерений №8.3 - 2017

 

Введение

Особую роль в обеспечении безопасной эксплуатации железнодорожного транспорта играет надежность верхнего строения пути, а именно рельсов, наличие опасных дефектов в которых может привести к сходу подвижного состава.

В общем случае прочность элементов конструкций и машин, а также их ресурс задаются на стадии разработки и проектирования. Однако воздействие на деталь знакопеременных нагрузок, коррозионных сред, колебаний температуры и наличие в материале детали технологических или эксплуатационных дефектов существенно снижают срок службы объекта [1–4]. Для предотвращения внезапного разрушения, вызванного развитием усталостных дефектов, проводят плановый неразрушающий контроль ручными дефектоскопами, автоматизированными вагонами-дефектоскопами и автомотрисами. Используемые методы и средства дефектоскопии ориентированы на выявление значительных по размерам, критически развитых дефектов [5, 6].

Одной из наиболее частых причин разрушения многих металлических конструкций, в том числе и рельсов, является высокий уровень остаточных напряжений, которые могут достигать предела текучести, особенно в области дефектов [6, 8]. Остаточные напряжения возникают в процессе производства, при механических и термических нагрузках, в процессе эксплуатации рельса, при сварке. Это приводит к тому, что в вершине трещины некритических размеров появляется концентрация напряжений, которая, суммируясь с остаточными технологическими напряжениями, приводит к ускоренному развитию трещины и существенно сокращает долговечность конструкции [8–11].

Цель работы заключалась в создании модели рельса с учетом термического упрочнения головки и подошвы и сопоставлении результатов моделирования с измерениями, полученными в ходе эксперимента. Знание величины внутренних напряжений в рельсах позволит получить информацию об их техническом состоянии, благодаря чему можно избежать аварийных ситуаций. Направление исследований является особо актуальным в связи с принятой стратегией развития холдинга «РЖД» на период до 2030 года.

Моделирование расхождения подошвы и головки рельса с разрезом

Технологии изготовления рельсов постоянно совершенствуются, так же как и методы неразрушающего контроля. Новая технология производства рельсов ДТ 350 из непрерывнолитой заготовки согласно ГОСТу 51685-2013 «Рельсы железнодорожные. Общие технические условия» при приемо-сдаточных испытаниях не допускает остаточных напряжений в шейке, приводящих к расхождению паза на торце полнопрофильной пробы рельса после ее прорезания по центру шейки, превышающему 2,0 мм. Пробу длиной 600 мм прорезают в холодном состоянии по нейтральной оси рельса на длину 400 мм с шириной паза 6 мм.

Используя нормативы ГОСТа 51685-2013 при моделировании напряженно-деформированного состояния рельса, можно получить ориентировочные допустимые значения остаточных напряжений, возникающих в рельсе после его изготовления. Полученные значения могут найти применение при дальнейшей верификации результатов расчета остаточных напряжений, полученных акустоупругим методом.

Моделирование осуществлялось в программной среде COMSOL Multiphysics. Для проведения моделирования использован подключаемый модуль «Механика твердых тел» с использованием методов конечных элементов и уравнений равновесия всей конечно элементной модели:

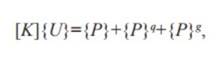
где [K] – общая матрица жесткости конечно-элементной модели; {P} – вектор заданных внешних узловых сил; {P}q и {P}g – общие векторы узловых сил, эквивалентных распределенным и массовым силам.

Обозначенное выше расхождение головки и подошвы рельса возникает вследствие возникновения остаточных напряжений при проведении термического упрочнения рельса. Остаточные напряжения в рельсе возникают из-за неравно- мерного охлаждения рельса и соответственно разной плотности металла в разных элементах рельса. При этом в подошве и головке рельса напряжения носят сжимающий характер, а в шейке рельса напряжения – растягивающий характер[7, 9, 10].

Для моделирования напряженно-деформированного состояния к подошве и головке рельса были приложены распределенные продольные силы, стремящиеся создать растягивающие напряжения в шейке и сжимающие в подошве и головке рельса (рисунок 1), что приводит к возникновению момента, обуславливающего расхождение паза.

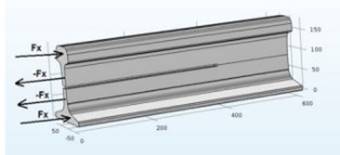
Рисунок 1 – Схематичное распределение приложенных сил

Ниже в качестве примера представлено распределение смещений точек рельса относительно равновесного состояния при значении расхождения паза 2 мм по вертикали (рисунок 2), что является максимально допустимым согласно ГОСТу 51685-2013. Согласно результатам моделирования данное значение наблюдается при значении силы Fx = 55 МН. Обработанные результаты моделирования расхождения паза в зависимости от значения распределенной силы представлены в таблице 1.

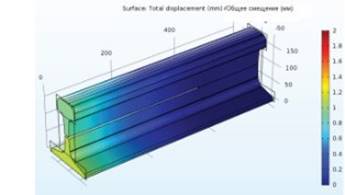
Рисунок 2 – Распределение смещений в рельсе при значении силы 55 МН.

 

Таблица 1

Расхождение паза в рельсе при различных значениях силы Fx

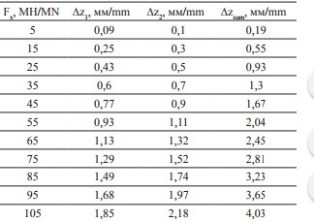
Fx – значение силы, приложенной к элементам рельса согласно схеме, приведенной на рисунке 1; ∆z1  – значение смещения головки рельса по вертикальной оси; ∆z2 – значение смещения подошвы рельса по вертикальной оси; ∆zsum – смещение головки рельса относительно подошвы по вертикальной оси (расхождение паза).

Максимально допустимому значению расхождения паза в 2 мм согласно ГОСТу соответствует значение распределенной продольной силы 55 МН.

Результаты моделирование напряженного состояния рельса

Для осуществления моделирования напряженного состояния к рельсу были приложены такие же значения распределенных сил, как и в моделировании расхождения паза. Пример распределения максимальных напряжений при значении силы Fx = 55 МН, что соответствует расхождению паза в 2 мм, представлен ниже (рисунок 3).

Примеры графиков распределения напряжений в продольном и вертикальном направлениях приведены на рисунках 4 и 5 соответственно. Результаты моделирования напряжений при значении расхождения паза в 2 мм представлены в таблице 2.

Анализ напряжений, возникающих в рельсе, подтверждает, что напряжения в продольном направлении пропорциональны приложенной силе, носят сжимающий характер для головки и подо швы и растягивающий для шейки. Аналогичное распределение можно наблюдать и в вертикальном направлении, однако согласно результатам моделирования напряжения в подошве и головке в данном случае не имеют больших значений в отличие от напряжений в шейке рельса, которые могут достигать больших значений.

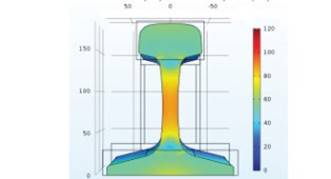
Рисунок 3 – Распределение максимальных напряжений в рельсе при Fx = 55 МН.

Таблица 2. Напряжения в рельсе при значении расхождения паза 2 мм

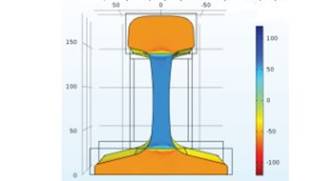
Рисунок 4 – Распределение напряжений в продольном направлении при Fx = 55 МН.

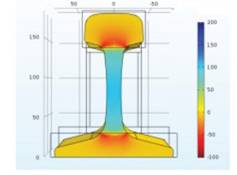
Рисунок 5 – Распределение напряжений в вертикальном направлении при Fx = 55 МН.

Производство рельс ведется из сталей марки Э76Ф, имеющей следующие физико-механические характеристики: модуль Юнга E = 207 ГПа, предел текучести σt = 1080 МПа. Как видно из таблицы 2, значения напряжений в рельсах значительно ниже предела текучести материала, однако в процессе эксплуатации идет процесс накопления остаточных напряжений, в результате чего напряжения в области дефектов могут достигать предела текучести [5, 6]. Нормирование значений напряжений при производстве рельсов позволяет увеличить срок службы изделий.

Описание методики эксперимента

Неразрушающий контроль напряженно-деформированного состояния тел осуществляется различными методами, однако в связи с особенностями конструкции рельсов появляются определенные ограничения, связанные с выбором методики контроля. Одним из наиболее перспективных методов контроля величины остаточных напряжений рельса является акустоупругий метод, успешно применяемый для контроля ободьев железнодорожных колес [10, 12, 13]. Для напряжений, определяемых по данному методу, существует следующая зависимость [6, 10, 12]:

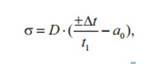
где D = 145 ГПа – коэффициент упругоакустической связи для одноосного напряженного состояния, определяемый экспериментально, a0 – параметр акустической анизотропии материала; Δt – разница между временем распространения сдвиговых волн, поляризованных в продольном и поперечном направлениях относительно оси рельса в напряженном состоянии, с; t1 – время распространения сдвиговой волны, поляризованной вдоль главных напряжений, с.

Структурная схема экспериментальной установки представлена на рисунке 6 [12]. Она включает в себя генератор электрических импульсов 2, формирующий мощный зондирующий электрический импульс в объекте контроля 1, электромагнитно-акустический преобразователь 3, возбуждающий и принимающий короткие акустические импульсы поперечных волн, усилитель 4 и плату АЦП 5, встроенную в ЭВМ, на экране которой отражается осциллограмма отраженных импульсов. Электромагнитно-акустический (ЭМА) преобразователь устанавливается на легкодоступную поверхность головки или шейки рельса [6, 14].

Данный метод является перспективным, и потому для проверки полученных результатов возникает необходимость в предварительном моделировании напряженно-деформированного состояния рельсов. Величина остаточных напряжений, как было сказано выше, зависит не только от наработки рельса, но и от технологии изготовления. Несмотря на это, метод проверки остаточных напряжений в рельсе согласно ГОСТу 51685- 2013 является универсальным для каждого типа рельс. За информативный параметр в данном методе используется увеличение расстояния между подошвой и головкой рельса при выполнении продольного выреза в рельсе на глубину 600 мм, а не значения напряжений в рельсе, в связи с чем возникает необходимость установить связь между двумя методами посредством проведения моделирования.

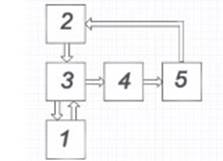
Рисунок 6 – Структурная схема установки: 1 – объект контроля; 2 – генератор; 3 – электромагнитно-акустический преобразователь; 4 – усилитель; 5 – ПК с платой АЦП.

Экспериментальные значения были получены струтуроскопом СЭМА, в основе которого лежит использование метода акустоупругости. Снятие осциллограмм производилось в программной среде ПРИНЦ [15], обработка полученных осциллограмм производилась в программной среде Sensitive, также входящей в пакет регистратора высокочастотных сигналов ПРИНЦ (св-во № 2011614594 от 21.04.2011) Измерения проводились по пяти отрезкам различных рельс, не находившихся в экспуатации. В качестве результатов моделирования взяты значения, полученные при расхождении паза в 2 мм. Результаты измерений представлены в таблице 3.

Таблица 3. Результаты измерения напряжений в рельсах.

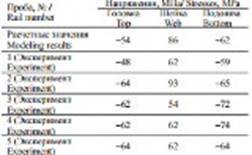
Погрешность измерения напряжений составляет около ±5 МПа, результаты измерений показывают довольно высокий уровень сходства с результатами моделирования. Также экспериментально подтверждается картина распределения напряжений в рельсе (растягивающие напряжения в шейке рельса, сжимающие в головке и подошве рельса).

 

Заключение

Разработана модель, позволяющая проводить анализ напряжений, возникающих в рельсе и связать эти напряжения с требованиями ГОСТа 51685-2013, где нормирование остаточных напряжений ведется с помощью учета расхождения головки и подошвы рельса. Смоделированы напряжения в рельсе при различном расхождении после прорезания паза в шейке.

Выполнено моделирование деформаций в рельсе после прорезания паза в шейке.

Приведено описание остаточных напряжений: в головке и подошве имеют место сжимающие продольные напряжения, в то время как в шейке рельса характер напряжений растягивающий как в продольном, так и в вертикальном направлении.

Результаты моделирования остаточных напряжений показали совпадение характера распределения напряжений с экспериментально полученными данными по пяти пробам рельсов.

 

Литература

1. Громов, В.Е. Микроструктура закаленных рельсов / В.Е. Громов, А.Б. Юрьев, К.В. Морозов, Ю.Ф. Иванов. – Новокузнецк : Изд-во «Интер-Кузбасс», 2014. – 213 с.

2. Бехер, С.А. Экспериментальная методика измерения динамических сил, действующих на рельсы подкранового пути в реальных условиях эксплуатации / С.А Бехер, А.О. Коломеец // Известия вузов. Строительство. – 2016. – № 3. – С. 110–118.

3. Неразрушающий контроль : справочник: в 7 т. / под общ. ред. В.В. Клюева. – Т. 4 : в 3 кн. Кн. 1: Акустическая тензометрия / В.А. Анисимов, Б.И. Каторгин, А.Н. Куценко [и др.]. – М. : Машиностроение, 2004. – 736 с.

4. Deputat, J. Experiences in Ultrasonic Measurement of Rail Residual Stresses / O. Orringer [et al.] (eds.); J. Deputat, J. Szelazek, A. Kwaszczynska-Klimek and A. Miernik // Residual Stress in Rails. – Kluwer academic publishers. – 1992. – No. 1. – Р. 169–183.

5. Степанова, Л.Н. Исследование напряженного состояния рельса с использованием акустоупругости и тензометрии / Л.Н. Степанова, С.А. Бехер, А.Н. Курбатов [и др.]. – Изв. вузов. Строительство. – 2013. – № 7. – С. 103–109.

6. Муравьев, В.В. Электромагнитно-акустический метод исследования напряженно-деформированного состояния рельсов / В.В. Муравьев, Л.В. Волкова, А.В. Платунов, В.А. Куликов // Дефектоскопия. – № 7. – 2016. – С. 12–19.

7. Иванов, Ю.Ф. Формирование структурно-фазовых градиентов в рельсах при длительной эксплуатации / Ю.Ф. Иванов, К.В. Морозов, О.А. Перегудов [и др.] // Проблемы черной металлургии и материаловедения. – 2015. – № 3. – С. 59–65.

8. Иванов, Ю.Ф. Эволюция структурно-фазовых состояний рельсов при длительной эксплуатации / Ю.Ф. Иванов, В.Е. Громов, О.А. Перегудов [и др.] // Известия высших учебных заведений. Черная металлургия. – 2015. – Т. 58. – № 4. – С. 262–267.

9. Покровский, А.М. Численное моделирование температурно-структурного состояния железнодорожного рельса при его закалке / А.М. Покровский, Д.Н. Третьяков // Наука и Образование. МГТУ им. Н.Э. Баумана. Электрон. журн. – 2015. – № 7. – С. 1–13.

10. Никитина, Н.Е. Применение метода акустоупругости для определения напряжений в анизотропных трубных сталях / Н.Е. Никитина, А.В. Камышев, С.В. Казачек // Дефектоскопия. – 2015. – № 3. – С. 51–60.

11. Whithers, P.J. Overview Residual stress / P.J. Whithers, H.K.H Bhadeshia. Part 1 – Measurement techniques // Material Science and Technology. – 2001. – Vol. 17. – P. 355–365.

12. Бехер, С.А. Использование эффекта акустоупругости при исследовании механических напряжений в рельсах / С.А. Бехер, А.Н. Курбатов, Л.Н. Степанова // Вестник РГУПС. – № 2. – 2013. – С. 104–110.

13. Schneider, E. Ultrasonic Evaluation of Stresses in the Rims of Railroad Wheels / E. Schneider, R. Herzer // NDTnet. – June 1998. – Vol. 3, no. 6.

14. Муравьев, В.В. Оценка остаточных напряжений в рельсах с использованием электромагнитно-акустического способа ввода-приема волн / В.В. Муравьев, Л.В. Волкова, В.Е. Громов, А.М. Глезер // Деформация и разрушение материалов. – 2015. – №12. – С. 34–37.

15. Стрижак, В.А. Информационноизмерительная система возбуждения, приема, регистрации и обработки сигналов электромагнитно-акустических преобразователей / В.А. Стрижак, А.В. Пряхин, С.А. Обухов, А.Б. Ефремов // Интеллектуальные системы в производстве. – 2011. – № 1. – С. 243–250.