Математическая модель размещения груза в контейнере

 

Лисицын Д.А. (кафедра ГЗТиЛ Донецкого национального технического университета, г. Донецк, Украина)

 

      Цель: Целью данной работы является выявление правил погрузки груза в контейнеры и создание математической модели размещения емкостей паралелепидной формы в контейнеры при учете максимальной  потребительской оценки.

 

 

       Введение

 

В наше время в связи с увеличением грузопотока важной  проблемой является развитие и разработка методов решения  задач маршрутизации, основной целью которой является понижение расходов при перевозке и доставке разных грузов [1, 2]. Подобные задачи относятся к транспортной логистике, которая включает: создание транспортных систем, планирование транспортных процессов на разных видах транспорта, обеспечение технологического единства транспортно-складского  процесса [3-5]. В статьях [6-8] рассматриваются задачи доставки грузов потребителям, которые сформулированы как многокритериальные задачи комбинаторной оптимизации. Для поиска кратчайшего пути доставки грузов используется интерактивная карта компании Яндекс, с помощью которой реализован алгоритм Дейкстры с учетом технологических ограничений. Для решения задач размещения грузов в транспортные средства (ТС) предложены эффективные методы: ролевая гиперэвристика и эволюционный алгоритм. Для задач размещения грузов в ТС проведены численные эксперименты на случайно сгенерированных данных и тестовых примерах из международной библиотеки тестов OR-library.

 

 

Изложение материала и результаты.

Введем следующие значения:  - множество заказчиков, C,k=1, …,  - подмножество множеств емкостей определяющие отношение между элементами множества V і C.

При этом, должны выполнятся условия:

.

Обозначим через  количество использованных при размещении емкостей паллет, а через множество P= - множество используемых паллет. Пусть P - подмножества емкостей, которые определяют отношение между элементами множеств V і P.

При этом, должны выполнятся условия:

.

Обозначим  - длинна, ширина и высота k-го контейнера, k=1,..., - количество используемых контейнеров;  - длинна, ширина и высота, соответствено,  i-й емкости, - координаты емкости на паллете (рис.1);  - масса i-й емкости,  - длинна, ширина и высота паллеты;- координаты j-й паллеты в контейнере (рис.2).

При размещении емкостей в паллете должны быть соблюдены следующие условия:

- грани емкостей параллельны граням контейнера;

- емкости не перекрывают друг друга:

∧

;

- емкости не выходят за границы контейнера

;

- общая масса емкостей на паллете не должна превышать грузоподъёмность  паллета и погрузчика:

 

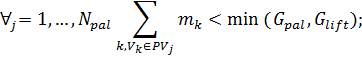
- на одной паллете должны находиться емкости только одного заказчика:

 

 

Рис.1. Обозначение координат и размеров объектов (ёмкость на паллете)

 

 

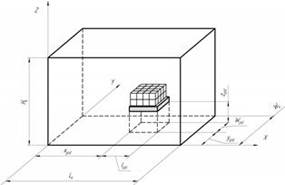
Ріс.2. Обозначение координат и размеров объектов (паллета в контейнере)

Введем емкости двух типов: однородные(Р_1) и неоднородные (Р_2). На паллетах типа Р_1 в одному ярусе высоты емкостей должны быть равными, а на паллетах типа Р_2 в одном ярусе могут находиться емкости разных высот.

Тогда условие размещения емкостей на паллетах можно записать в виде:

При размещении емкостей по паллетам желательно, чтобы все емкости выявлялись в подмножестве Р_1,и каждый ярус был заполненный полностью. При этом обеспечивается максимальная стойкость грузов. Но при реальных условиях исполнения данного условия зависит от количества емкостей разных высот, от их разнообразности и других показателей. Для решения этой проблемы вводят коэффициент заполненной паллеты: 0.

Если отношение  занятой площади в ярусе преувеличивает, то пространство, которое остается, может быть заполненным специальными прокладками (рис.3а).

 

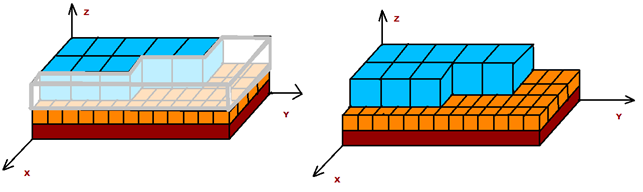
а                                             б

 

Рис.3.Пример заполнения яруса на паллете  м однородными грузами.

 

Иначе, емкостей одинаковой высоты оказывается  недостаточно для заполнения всей площади яруса (рис. 3б).

А это означает, что эти емкости размещают на паллете типа Р_2. Значения коэффициента  зависит от типа емкостей, их крепости и других характеристик.

При выполнении всех условий нужно минимизировать количество контейнеров.

 

Вывод. В данной статье рассмотрены правила погрузки груза в контейнер и  рассмотрена математическая  модель (алгоритм) плотного размещения  емкостей, которые имеют  форму параллелепипеда. Было найдено  такое размещение в ТС, при котором количество используемых ТС будет минимальной при соблюдении технологических ограничений, таких как: стойкость грузовых единиц, нахождение на паллете емкостей одного заказчика, при условии соответствия массы груза и грузоподъёмности паллет.

 

 

 

 

 

 

Литература

 

1. Миротин Л.Б. Логистика интегрированных цепочек поставок : учебник / Л.Б. Миротин, А.Г. Некрасов. - М.: Изд-во «Экзамен», 2003. –256 с.

2. Лукинский В.С. Модели и методы теории логистики / В.С. Лукинский, В.В. Лукинский, Ю.В. Малевич; под ред. B.C. Лукинского. - СПб.: Изд-во «Питер», 2007. –448 с.

3. Будішевський В.О. Транспортно-складська логістика гірничих підприємств / В.О. Будішевський, В.О. Гутаревич, Л.Н. Ширін та ін.; ред. В.О. Будішевський, Л.Н. Ширін. – Д.: Національний гірничий університет, 2010. – 433с.

4. Будишевский В.О. Транспортно-технологическая логистика энергоёмких производств / В.О. Будишевский, В.О. Гутаревич, В.О. Кислун и др.; ред. В.О. Будишевский, А.О.Сулима. – Донецк: РВА ДонНТУ, 2003. – 302с.

5. Gutarevich V. Strefy serwisowe centrów transformacyjnych / V.Gutarevich, A.Ovcharenko, V.Zhuchenko // Problemy transportu. Wydavnictvo Politechniki Slaskiej. Gliwice. – 2009. Tom 4. Zeszyt 3. Czesc 1.– Str. 53-57.

6. Юсупова Н.И., Валеева А.Ф., Рассадникова Е.Ю., Латыпов И.М., Кощеев И.С. Многокритериальная задача доставки грузов различным потребителям / Н.И.Юсупова,А.Ф. Валеева, Е.Ю.Рассадникова и др. // Логистика и управление цепями поставок. – 2011. – №6. –С. 60-82.

7. Bettinelli A., Ceselli A., Righini G. A branch-and-cut-and-price algorithm for the multi-depot heterogeneous vehicle routing problem with time windows// Original Research Article, Transportation Research Part C: Emerging Technologies. – 2011. – Volume 19. – Issue 5. – P. 723-740

8. Dondo R., Cerdá J. A cluster-based optimization approach for the multi-depot heterogeneous fleet vehicle routing problem with time windows // European Journal of Operational Research. – 2007. – Volume 176. – Issue 3. – P. 1478-1507