Динамика мостового крана. Часть 1. Определение характеристик мостового крана

Авторы: Сладковский А., Ханишевский Т., Матыя Т.

Вестник Восточноукраинского национального университета им. Даля№1, 2010. 200-206.

 

Вступление

 

Мостовые краны являются обязательным элементом большинства предприятий, в которых выполняются ремонты тяжелой транспортной техники. Очевидно, что различные депо, локомотиво- и вагоноремонтные заводы относятся к числу таких предприятий. К сожалению, большая часть грузоподъемной техники не является новой, поскольку обычно такая техника проектируется и потом работает многие годы. Чаще всего расчеты такой техники выполнялись достаточно давно, когда современные методы исследования были еще не доступны. Однако и в настоящее время рассмотреть динамическую модель такого оборудования является достаточно сложной задачей. В рассматриваемой статье сделана попытка применить достижения современных численных методов расчета для моделирования подъема грузов при помощи мостового крана. Предлагаемая работа является несмотря на свой утилитарный характер может иметь ценность методологическую, поскольку рассматриваемые методики расчета могут с успехом быть использованы для моделирования других динамических систем, например, движения поезда, взаимодействия пути и подвижного состава и т.д.

Задачей статьи было рассмотреть динамические явления, происходящие при подъеме грузов. Подобные задачи рассматривались ранее [1], однако проблемой обычно было определение распределения приведенных масс, поскольку конструкция мостового крана, несмотря на свою относительно высокую жесткость, также участвует в динамическом процессе. Использование метода конечных элементов (МКЭ) позволяет уточнить вопросы, связанные с распределением масс и жесткостей, и, выполнив их редукцию, определить приведенные массы. С этой целью в задании использовались гибридные расчета с использованием программного обеспечения ABAQUS/MATLAB/SIMULINK. Благодаря использованной методике удалось получить существенную информацию о поведении конструкции во время подъема грузов. Получена также возможность исследования отдельных мест конструкции с целью определения частоты вибраций, которые могут быть опасными для человека, зданий или самой конструкции крана.

 

Геометрическое моделирование мостового крана

 

Зачастую для эксплуатирующихся конструкций мостовых кранов сложно найти соответствующую конструкторскую документацию. На рис. 1 представлена геометрическая модель мостового крана, для которой конструкторская документация была разработана фирмой OBRDiUT – Bytom. Это двухбалочный мостовой кран с грузоподъемностью 20 т и пролетом моста 34,5 м. Проектирование рассматриваемой конструкции было основано на использовании стандартов [2, 3]. Указанная конструкция выбрана потому, что она является достаточно распространенной в различных транспортных предприятиях. Подобные конструкции описаны в книгах [4, 5].

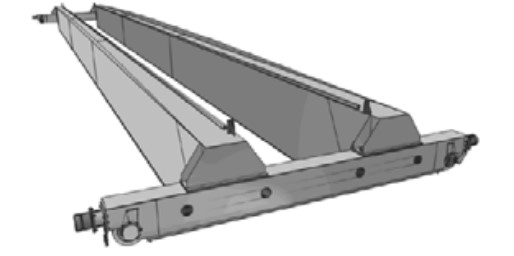
Рис. 1. Геометрическая модель мостового крана

Исследуемая металлоконструкция является сварной листовой балочной конструкцией, которая присуща высокая грузоподъемность. Первым подготовительным этапом перед началом создания конечно-элементной (КЭ) модели являлось упрощение рассматриваемой геометрии. Известно, что определенные детали, которые необходимы для правильной эксплуатации конструкции могут ничего не менять в ее напряженно-деформированном состоянии. Это же относится и к необходимости устранения дополнительных малых отверстий, фасок, скруглений и пр. конструктивных элементов, влияние которые на прочностные свойства конструкции могут быть незначительны, а с другой стороны их наличие может способствовать генерации КЭ сеток имеющих большую густоту. Известно, что каждый лишний узел создает лишние степени свободы КЭ модели. Следует по возможности стараться оптимизировать КЭ сетки. Например, если есть такая возможность использовать линейные или плоские элементы вместо пространственных. Но самое главное состоит в том, что в задачу авторов не входила оценка напряженно-деформированного состояния рассматриваемого мостового крана, тем более, что сомнений в его работоспособности нет, поскольку он успешно эксплуатируется. Задачей авторов была оценка жесткостных характеристик крана с тем, чтобы далее использовать эти данные для анализа динамики подъема груза.

На рис. 2. показан пример упрощения геометрической модели перед генерацией КЭ сетки.

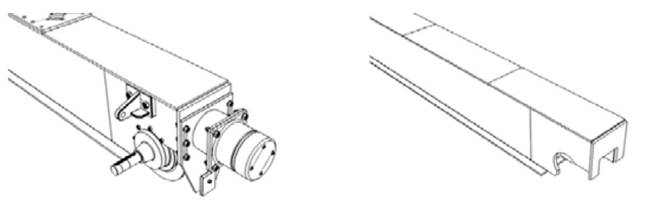
Рис. 2. Упрощение геометрической модели мостового крана перед генерацией КЭ сеток

КЭ модель мостового крана

В качестве основного инструмента КЭ анализа использовался пакет ABAQUS. Для создания КЭ модели использовались оболочечные элементы типа Shell с узлами, имеющими 6 степеней свободы. При этом основными КЭ элементами были элементы типа S4 и S3, соответственно, с 4 и 3 узлами, которые имели средний размер 50 мм. Указанный средний размер использовался для проведения автоматической генерации основной КЭ сетки. В результате дискретизации была создана КЭ сетка, состоящая из 170644 конечных элементов. При этом элементы создавались для отдельных конструкционных элементов, имеющих различную толщину. Соответственно, каждому элементу в зависимости от принадлежности к определенной детали приписывалась толщина и материал. Основным материалом рассматриваемой конструкции являлась сталь. В связи с тем, что материал мостового крана работает в упругой области, для заданного в модели материала использовались только его упругие характеристики:

•  коэффициент Пуассона равный 0.3;

•  модуль Юнга 2,1*10 5 [МПа];

а также

•  плотность материала 7,85*10 -9 [т/мм 3 ].

Опоры концевых балок перенесены из точек, находящихся на оси приводных валов непосредственно на конструкцию концевых балок при помощи элементов типа RIGID, а точнее COUP_KIN (сокращение от английского Coupling Kinematic). Для того чтобы приложить силы, действующие на металлоконструкцию, использована модель рельсов, по которым движется тележка грузоподъемного механизма. Рельс был упрощенно представлен в виде набора линейных балочных элементов (B31). Для данных элементов был задан ряд специфических свойств, который в программе называется BEAMSECTION, таких как:

•  форма поперечного сечения рельса (BOX – рассматриваемая конструкция крана использует рельса, приваренные к верхнему листу главных балок; при этом в качестве рельсов используется прокатный профиль квадратного поперечного сечения с заданной толщиной стенок);

•  размеры поперечного сечения. На представленном рис. 3 с целью большей наглядности моделирования балочных элементов были убран ряд слоев поверхностных элементов, а именно для одной из балок элементы боковых листов, а также верхнего листа. Это также позволяет увидеть внутреннюю структуру главных балок моста с их ребрами жесткости.

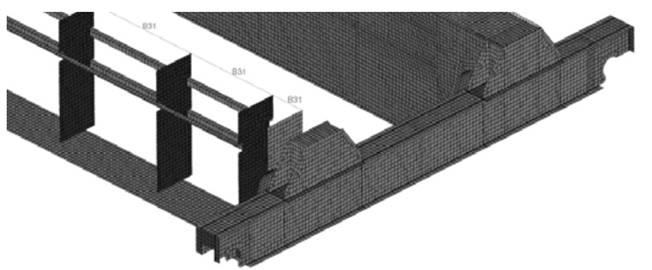
Рис. 3. Моделирование рельсов для движения тележки (элементы B31)

К описанной выше модели добавлены массовые элементы, дополнительные внешние силы, а также задана гравитация, что должно учесть действие собственной массы, а также массу тележки совместно с грузоподъемным механизмом и поднимаемым грузом. Массовые элементы типа MASS позволяют учесть указанные силовые факторы. Силы, также как и массовые элементы были заданы в местах контакта колес тележки и рельсов в среднем ее положении.

Расчетный процесс был поделен на четыре этапа. На первом этапе исследуется влияние гравитации, на втором добавляется действие массы тележки, на третьем учитывается действие силы инициированной подъемом рассматриваемого груза, и наконец, проводится модальный анализ нагруженной конструкции. С целью определения жесткости моста проведен еще один дополнительный расчет (новое моделирование), для которого моделируется исключительно действие нагрузки, связанной с подъемом груза, без учета гравитации.

Определение собственных частот колебаний мостового крана и оценка жесткости металлоконструкции

На рис. 4 представлена модель рассматриваемого мостового крана, где показаны места приложения сил и масс (5), а также места закрепления (1-4) – граничные условия. В области опор 1, 2 убраны 6 степеней свободы, а на опорах 3, 4 устранены только 2 возможности перемещения узлов: в направлениях осей y и z.

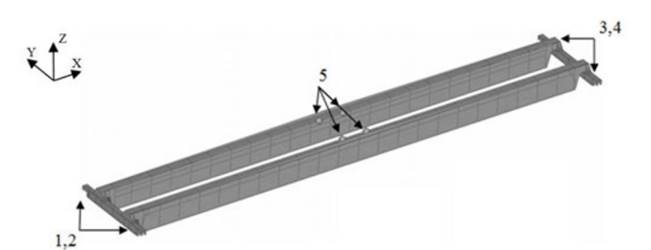
Рис. 4. Задание граничных условий

Расчеты показали, что величина статического прогиба ненагруженной конструкции (под действием собственной массы) составляет посередине между опорами u st =-20,93 мм. В случае догрузки конструкции поднимаемым грузом 20 т статический прогиб становится равным u st =-38,41 мм. Если же рассматривать ту же самую задачу без учета сил тяжести действующей на конструкцию крана, но оставляя силу от действия поднимаемого груза, то прогиб будет равен u st =-17,47 мм. Последние данные используются для нахождения жесткости конструкции мостового крана при центральном расположении механизма подъема груза.

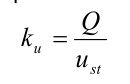
, где ust – прогиб моста, Q – сила тяжести поднимаемого груза. Подстановка расчетных данных в формулу (1) дает следующий результат: k u =11,23*10⁶ Н/м.

Важным моментом исследования динамики работы мостового крана является определение собственных частот и форм колебаний. Указанные данные позволяют устранить возможность проявления резонансных явлений, что может быть небезопасно как для процесса подъема груза, так и для работы крана в целом. Средства КЭ программного обеспечения позволяют провести модельный анализ рассматриваемой металлоконструкции. Такой анализ было проведен и в табл. 1 представлены восемь низших собственных частот колебаний и соответствующие им формы колебаний.

Низшие собственные частоты и соответствующие собственные формы

Заключение

В работе проведено исследование реальной металлоконструкции мостового крана. Определены жесткость, собственные частоты и формы колебаний. В следующей части планируется использовать полученные данные для анализа динамики подъема груза с учетом упругих деформаций самой металлоконструкции.

Список литературы

1. Sładkowski A., Matyja T.: Modelowanie drgań suwnicy spowodowanych podnoszeniem ładunku; Brno 2007.

2. Norma PN-EN 13001-2: 2004: Bezpieczeństwo dźwignic. Ogólne zasady projektowania; Część 2: Obciążenia.

3. Norma PN-ISO 8686-1: 1999: Dźwignice. Zasady obliczania i kojarzenia obciążeń. Postanowienia ogólne.

4. Piątkiewicz A., Sobolski R.: Dźwignice tom I; WNT, Warszawa 1969.

5. Zieliński Z.: Dźwignice i urządzenia transportowe; PWSZ, Wrocław 1972.