Оценка разрушительной способности импульса нагрузок

Аннотация

Комаров А., Громов Н., Соколова Ю. — Оценка разрушительной способности импульса нагрузок Статья дает краткий обзор методологии, чтобы найти динамические коэффициенты нагрузок импульса, типичных для различных чрезвычайных ситуаций (взрывчатый взрыв, массивное падение тела, гидравлический шок, и т.д.). Критерии описанный, под которым динамические коэффициенты определены импульсом воздействуйте один не важный из его формы. Корреляции, как указывают, считают динамичным коэффициенты для нагрузок воздействия, которые сопровождают такие чрезвычайные ситуации.

ВВЕДЕНИЕ

Это — принятая практика строительного дизайна, до которого уменьшены нестатические нагрузки, эквивалентные статические нагрузки. Вычисления динамического воздействия на конструкции здания используют следующая методология. Динамические нагрузки заменяют с его эквивалентными статическими найденными нагрузками этой формулой [1, 2, 3]:

где P maxс — максимальная динамическая ценность груза; Кd—динамический коэффициент, равный максимальной ценности динамической функции Т (t), который описывает движение структуры (ее секции перемена) вовремя.

Как очевидно от (2.2.1), чтобы заменить динамическим грузом с его эквивалентным грузом мы нуждаемся знать динамический фактор Кd .

Например, динамический коэффициент Кd для груза треугольной формы часто известен из диаграмм (Рис. 1), доступный во многих справочных руководствах по вычислению силы структуры, где О и О1 — продолжительность динамического груза и время это берет, чтобы достигнуть максимума; wК -частота главного колебания делает подачу в структуре, найденной использованием методов конструктивной механики.

Диаграмма означает это если O1 склоняется к нолю (пилообразная форма нагрузки), тогда динамическое числовое значение коэффициента приближается 2. Рассматривая это, проектировщики удваивают любой зуб пилы загрузите, когда они делают статические вычисления. Однако, этот подход является неправильным для краткосрочного импульс н. Это — проблема, обсужденная в этой cтатье.

Рисунок 1 — Схемы динамического коэффициента Кd.

Чрезвычайные ситуации создают мгновенные нагрузки скорее часто. Разрядка взрывчатого вещества материал или воздействие массивного падения корпуса (например, контейнеры транспортировки, падающие в охлаждении объединение атомной электростанции), или гидравлический шок и т.д. создает нагрузки, для которых это длится миллисекунды в очень высоком давлении.

Давайте исследуем динамическую методологию фактора на такие нагрузки. Это обсуждение будет придерживайтесь подходов, принятых в структурной динамике.

Мы знаем, что движение структуры в упругой стадии деформации описано уравнение:

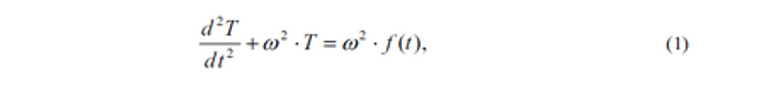
где w - круглая частота собственных вибраций структуры круговая частота; f(t)— функция, чтобы описать изменения во время безразмерных T(t)=S(t)/SМАКС — относительное движение структуры, или динамическая функция; Smax — смещение структура, отвечающая на статическую нагрузку — Рmax.

Решение уравнения (1) с нулевыми начальными условиями появляется как:

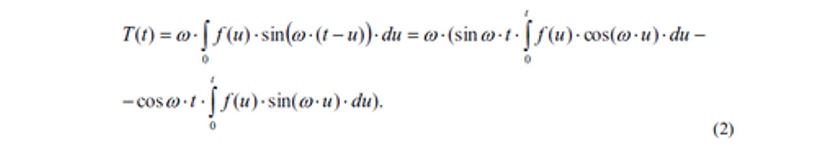
Численное интегрирование выражения (3) производит функцию структуры движение в отвечающем времени вызывает f(t). Максимальное значение функции смещения T(t)- динамический коэффициент Kd.

Чтобы найти динамический коэффициент, мы должны знать частоту структуры собственная подача колебания — w, выраженный формулой [4]:

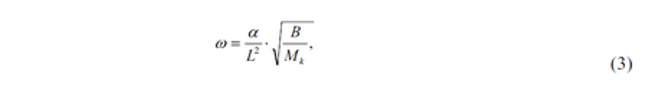
Уравнение (1) может быть решено, решая в цифровой форме эту систему дифференциальных уравнений:

У этого метода есть следующее неудобство. Расчеты предполагают что процесс колебание каждого элемента использует определенную частоту (как правило та из подачи), хотя в колебания действительности происходят через весь спектр собственных частот резинки элемент. Кроме того произвольные ограничивающие условия могут быть установлены с приближением в этом метод, но вычислить силу конструкций здания в чрезвычайной ситуации, когда максимум возможные нагрузки приняты как входы, даже при том, что они маловероятны, этот подход к вычислите Kd оправдан до степени.

Уравнение (1) было объединено для нескольких типов нагрузки и для различных передаточных чисел нагрузки продолжительность (Тload) к собственному периоду колебания структуры (Т0).

Рис. 2 дает значения динамических коэффициентов для различных передаточных чисел продолжительности нагрузки (Тload) к собственный период колебания структуры (Т0), и для пяти типов нагрузки. Очевидно, временное природа нагрузки — влияние на динамический фактор только для продолжительности нагрузки к колебанию передаточные числа периода, больше чем 0.5*Т0. Этот факт фактически иллюстрирован в Рис. 1, подготовленном основанный на довольно длинные нагрузки (относительно собственного периода колебания структуры), но не на импульсе нагрузки.

Рис. 3 дает значения динамических коэффициентов для различной продолжительности нагрузки к колебанию передаточные числа периода, К=0 для ударной нагрузки, и К=1 для типа нагрузки, у которого только есть фаза наращивания. Условно они могут быть расценены как чрезвычайные формы: ударная нагрузка и гладкая нагрузка.

.

Рисунок 2 — Динамические коэффициенты для пяти типов нагрузки.

Рисунок 3 — Динамические коэффициенты для двух чрезвычайных типов нагрузки.

Как указано выше (см. Рис. 2), для передаточных чисел ТНАГРУЗКИ/Т0<0.5, форма нагрузки не делает затроньте числовые значения динамических коэффициентов. Они, главным образом, под влиянием давления импульс:

IP(t)dt. Это замечено по результатам в Рис. 4, который указывает динамичный коэффициенты для формуемых треугольником нагрузок (I=Pmax*Тload) и для формуемых прямоугольником нагрузок (I=Pmax*Тload).

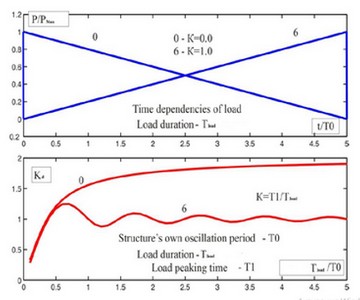
Рисунок 4 — Динамические коэффициенты для передаточных чисел ТНАГРУЗКИ/Т0<0.5 и для треугольника — и формуемые прямоугольником нагрузки

Расчет продемонстрировал, что динамический коэффициент для кратких нагрузок (Тload/Т0<0.5) может быть приблизительно найденный использованием этой формулы:

Например, в случае формуемой треугольником нагрузки (I=0.5*Pmax*Тload), динамическое коэффициент будет приблизительно равняться:

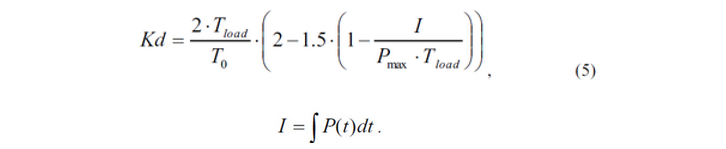
и для формуемой прямоугольником нагрузки (I=Pmax*Тload) динамический коэффициент:

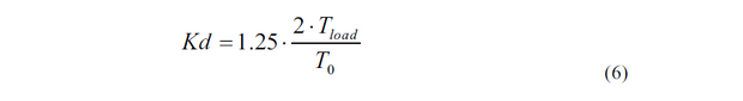
ВЫВОДЫ

Работа рассматривает специфические особенности вычисления динамических коэффициентов для типичных нагрузок импульса из многих чрезвычайных ситуаций. Критерии описаны, под которым динамические коэффициенты зависят только ударной нагрузкой импульс, но не его формой профиля.

Бумага дает передаточные числа, должен был вычислить динамические коэффициенты для ударных нагрузок это сопровождайте чрезвычайные ситуации (разрядка взрывчатых материалов, массивного падения корпуса, гидравлический шок и т.д.).

Список использованной литературы

1. N. Popov, B. Rastorguyev, Dynamic Calculation for Reinforced Concrete Structures, Мoscow, Stroyizdat, 1974.
2. B. Rastorguyev, Methodological Guidance on Design and Examination of New and Existing Structures in Explosive Production Facilities (Version 1), Мoscow, 1996.
3. A. Komarov, Forecasting Loads and Estimating Consequences of Their Impact on Buildings and Structure. Moscow State Construction University National Research University, Moscow, 2001.
4. А. Abrosimov, A. Komarov, Oil, Gas and Bus., 6, 58-61, 2002