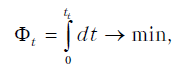
В.О. Гутаревич, Е.Л. Игнаткина

Рассмотрены проблемы эксплуатации шахтных подвесных монорельсовых дорог. Цель работы заключается в повышении эффективности работы и безопасности эксплуатации шахтной подвесной монорельсовой дороги за счет оптимизации переходных процессов, возникающих во время разгона или торможения подвижного состава. Для этого с учетом управляющих воздействий разработана математическая модель движения подвижного состава, установлен критерий оптимальности управления, составлен гамильтониан системы, получена сопряженная система уравнений и ее решение. Установлено, что во время пуска и торможения подвижного состава возникают дополнительные динамические нагрузки, которые через подвеску монорельсового пути передаются на крепь горной выработки. Определен оптимальный режим торможения шахтной подвесной монорельсовой дороги. Найдены зависимости между параметрами подвижного состава и тормозными усилиям. Полученные зависимости позволяют устанавливать целесообразное время включения или отключения тормоза подвижного состава, когда в первоначальный момент еще действует тяговое усилие, частично гасится скорость движения, а затем в момент отключения тяги производится дополнительное торможение до нулевой скорости. Это дает возможность минимизировать время торможения, повысить эффективность и безопасность работы шахтной подвесной монорельсовой дороги.

Ключевые слова: монорельсовая дорога, подвижной состав, динамические нагрузки, пуск, торможение.

Введение

Эффективность эксплуатации шахтных подвесных моно­рельсовых дорог тесным образом зависит от процессов, протекающих при пуске и торможении подвижного состава. Во время его разгона и остановки возникают динамические процес­сы, появляются дополнительные нагрузки, которые действуют на монорельс и его подвеску. Указанные нагрузки передаются на крепь горной выработки, снижая ее устойчивость. Поэтому исследование процессов, происходящих во время пуска и тор­можения подвижного состава шахтной подвесной монорельсо­вой дороги, является важной и актуальной задачей.

Состояние вопроса

Оценка эксплуатационных параметров шахтных подвесных монорельсовых дорог и вопросы повышения эффективности их работы рассмотрены в работах [1, 2]. Авторами предложены ресурсосберегающие технологические схемы комплексного ис­пользования адаптивных возможностей подвесных дизельных монорельсовых дорог для интенсификации подготовительных работ и повышения темпов отработки выемочных столбов в сложных горно-геологических условиях при разработке тонких угольных пластов. Задачей исследований [3 5] стала раз­работка методик расчета параметров анкерной подвески шахт­ной монорельсовой дороги, которые позволяют обоснованно определять нагрузки в системе «анкер-подвеска-монорельс». В работе [6] установлены особенности формирования дополнительных нагрузок от действия подвесных монорельсовых дорог на анкерную крепь горных выработок, рассмотрены условия взаимодействия подвижного состава монорельсовой до­роги и массива горных пород. Кроме того приведены результаты шахтных исследований, в которых получены зависимости изменения дополнительных нагрузок от действия подвижного состава монорельсовых дорог на арочное крепление. В работах [7, 8] проведены теоретические исследования процесса взаимодействия подвесного состава и монорельсового пути. Установлены пределы изменения координат и скорости движения составных частей подвесной монорельсовой дороги. Найдено влияние упруго-диссипативных связей на параметры движения во время торможения подвесного состава. Исследовано движение подвесных экипажей, перевозящих по монорельсо­вому пути крупногабаритный груз. Установлено, что продоль­ные динамические силы более чем в 1,6 раза могут превышать значение прикладываемых тормозных усилий. Возникающие во время торможения перевозимого груза отклонения отно­сительно вертикали периодически изменяются в пределах от 0,05 до 0,67 рад. Для снижения колебаний достаточно увели­чивать значение коэффициента демпфирования сцепок только тормозных тележек, что позволяет не усложнять конструкцию подвижного состава.

Выделение нерешенной части проблемы

Современные тенденции развития монорельсового транспор­та характеризуются стремлением к повышению массы грузовой единицы от 32 т до 40 т и скорости движения подвижного состава от 1,5 м/с до 4,0 м/с. Часто углы наклона монорельсового пути в горных выработках достигают 18° и более. Все это приводит к росту динамических нагрузок, возникающих во время разгона и торможения шахтной подвесной монорельсовой дороги.

Во время движения подвижного состава в режиме тяги или торможения возникают как растягивающие, так и сжимающие силы, направленные вдоль монорельса и приводящие к про­дольным колебаниям подвесной монорельсовой дороги. Воз­никающие при этом динамические нагрузки передаются на монорельсовый путь через тележки и сцепки. Кроме того про­дольные нагрузки воспринимают элементы подвижного соста­ва и перевозимый груз.

Проблемы, связанные с реализацией торможения подвижно­го состава, который перемещается по рельсам, расположенным на почве горной выработки, исследованы достаточно глубоко. Однако подвижной состав и путь монорельсовых дорог имеют существенные отличия, что не позволяет в полной мере исполь­зовать полученные ранее результаты. Для совершенствования шахтных подвесных монорельсовых дорог необходимо учиты­вать динамические процессы, протекающие во время ее дви­жения.

Цель статьи

Заключается в повышении эффективности работы и безопас­ности эксплуатации шахтной подвесной монорельсовой дороги за счет оптимизации переходных процессов, возникающих во время торможения подвижного состава.

Постановка задач

Для достижения указанной цели необходимо решить следу­ющие задачи:

разработать математическую модель движения подвижно­го состава с учетом управляющих воздействий;

установить критерий оптимальности управления;

определить характерные моменты времени изменения управлений, которые позволяют минимизировать время торможе­ния и установить целесообразное время включения или отклю­чения тормоза.

Изложение основного материала

Одним из путей снижения дополнительных динамических нагрузок, возникающих во время пуска и торможения подвиж­ного состава, является оптимизация переходных процессов. Это возможно благодаря созданию управляемых пусковых и тор­мозных устройств, имеющих возможность в широких пределах регулировать тяговые и тормозные усилия.

Особенно важна оптимизация процессов торможения, опре­деляющая эффективность и безопасность работы. При этом ос­новными параметрами переходных процессов, происходящих во время торможения и остановки, являются максимальные динамические нагрузки, деформации и амплитуды колебаний элементов подвижного состава, монорельса и подвесок.

Для определения оптимального управления минимизируется время на торможение подвижного состава из некоторого на­чального состояния в конечное. В этом случае критерий опти­мальности может быть установлен функционалом.

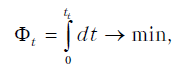
где dt – время торможения из начального состояния в конечное состояние (до полной остановки). С учетом этого установим режим оптимального торможения подвижного состава, который движется вдоль прямолинейно¬го монорельса под действием тягового усилия и сил трения, пропорциональных скорости

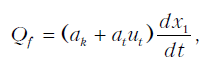
где a_k, a_t – коэффициенты пропорциональности, равные a_k > 0; a_t > 0; u_t – управление, определяющее силу трения тормозной тележки шахтной подвесной монорельсовой дороги; x₁ – коор¬дината движения подвижного состава при торможении. Обозначим действующее тяговое усилие как u_d, массу подвижного состава – m, а скорость движения через x₂. Тогда уравнения движения можно представить как систему

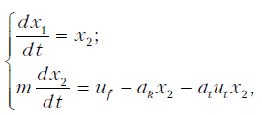
при следующих граничных условиях:

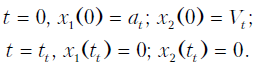
На тяговое и тормозное усилия в рассматриваемой динамической системе наложены ограничения 0< u_t< 1; |u_d| < 1. С учетом этого найдем управление u_t, при котором функционал ?_t принимает наименьшее значение. Используя подходы [9, 10] составим гамильтониан системы

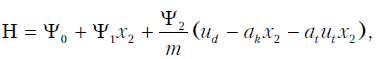
где ψ0, ψ1, ψ2, вспомогательные сопряженные переменные. Сопряженная система уравнений имеет вид

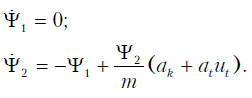
Решая эту систему, получим

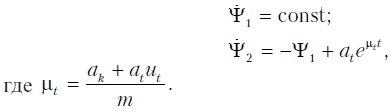
Режим торможения будет оптимальным, если принимает максимальное значение

График оптимального управления торможения приведен на рисунке. Из этого рисунка видно, что для интервала времени [0, t_k] , управления u_t(t) и u_d(t) имеют рад характерных точек. На указанном интервале времени управлению u_t(t) присущи две точки переключения, а управлению u_d(t) – одна. Кроме того, одной точке переключения управления u_t(t) соответствует одна точка переключения u_d(t). Установим характерные моменты времени изменения управлений. Для этого произведем интегрирование уравнений движения при оговоренных граничных условиях. В результате получим

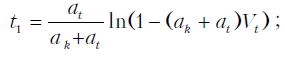
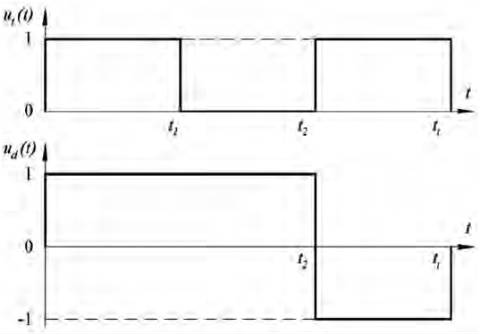
График оптимального управления торможением подвижным составом подвесной монорельсовой дороги

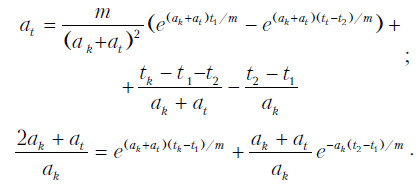
Полученные зависимости позволяют минимизировать вре¬мя торможения, устанавливать целесообразное время включе¬ния или отключения тормоза. Так, при торможении подвиж¬ного состава, когда в первоначальный момент еще действует тяговое усилие, частично гасится скорость движения, а затем в момент отключения тяги производится дополнительное торможение до нулевой скорости. При этом возможно реверсирование тягового усилия.

Выводы

На основании проведенных исследований получены зависимости, устанавливающие взаимосвязь между параметрами движения подвижного состава и тормозными усилиями. Разработана математическая модель движения и составлен гамильтониан системы. Найдены характерные моменты времени изме¬нения управлений, которые позволяют минимизировать время торможения и установить целесообразное время включения или отключения тормоза. Определен оптимальный режим торможе¬ния подвесного состава, что обеспечивает повышение эффек¬тивности и безопасности работы шахтной подвесной монорель¬совой дороги.

Список литературы

1. Ширин Л. Н., Расцветаев В. А., Коваль А. И. Повышение эффек¬тивности работы монорельсовых дорог при подготовке запасов угля к очистной выемке: монография. – Д.: НГУ, 2014. – 144 с.
2. Ширин Л. Н., Посунько Л. Н., Расцветаев В. А. Оценка эксплуатаци¬онных параметров подвесных монорельсовых дорог / Геотехнічна ме-ханіка: Міжвід. зб. наук. праць. Ін-т геотехнічної механіки ім. М.С. По-лякова НАН України. – Дніпропетровськ, 2008. – Вип. 76. – С. 91–96.
3. Ногих В. Р. Методика и алгоритм расчета параметров анкер¬ной подвески шахтной монорельсовой подвесной дороги // Уголь. – 2011. – № 5. – С. 84–85.
4. Расцветаев В. А. Дополнительные нагрузки от действия подвес¬ных монорельсовых дорог на арочное крепление выработок в услови¬ях шахт Западного Донбасса / Геотехнічна механіка: Міжвід. зб. наук. праць. Ін-т геотехнічної механіки ім.М.С. Полякова НАН України. – Дніпропетровськ, 2014.– Вип.117. – С. 53–59.
5. Хлусов А. Е. К расчету параметров анкеров, служащих для подве¬шивания монорельсовой дороги к кровле горной выработки / Сборник научных трудов ВНИМИ // Под ред. Д. В. Яковлева. – СПб.: ВНИМИ, 2012. – С. 317–322.
6. Кузнецов Е. В. Метод выбора параметров сталеполимерных анке¬ров для подвески монорельсовых дорог большой грузоподъемности в выработках // Вестник КузГТУ. – 2005. – № 4. – С. 27–28.
7. Гутаревич В. О. Продольная динамика шахтной подвесной моно¬рельсовой дороги // Науковий вісник НГУ. – 2015. – № 1. – С. 83–88.
8. Гутаревич В. О. Динамика шахтных подвесных монорельсовых дорог: монография. – Донецк: ЛАНДОН-ХХІ, 2014. – 206 с.
9. Понтрягин Л. С., Болтянский В. Г., Гамкрелидзе М. В., Мищен¬ко Е. Ф. Математическая теория оптимальных процессов. – М.: Наука, 1983. – 392 с.
10. Сухарев Э. А. Параметрическая оптимизация машин и оборудо¬вания. – Ровно: НУВХП, 2007. – 179 с.

Коротко об авторах Гутаревич Виктор Олегович – кандидат технических наук, доцент, e-mail: gvodonntu@gmail.com
Игнаткина Евгения Леонидовна – ассистент, e-mail: sel_post@mail.ru
Донецкий национальный технический университет, Украина.

Gornyy informatsionno-analiticheskiy byulleten’. 2016. No. 9, pp. 29–36.

V.O. Gutarevich, E.L. Ignatkina

JUSTIFICATION OF OPTIMAL MODE STARTING AND BRAKING OF MINE SUSPENDED MONORAIL The article deals with the problem exploitation of mine suspended monorails. Objective is to increase the efficiency and safety of operation mine suspended monorail through the optimization of transition that occur during acceleration or deceleration of the rolling stock. Taking into account the operating influences, were developed mathematical model of rolling stock, determined criterion for the optimal control system, composed Hamiltonian of system, obtained conjugate system and solution of equations. Established that during starting and braking of the rolling stock raises additional dynamic loads, by which the suspension monorail track are transmitted to the mine barring. Determined the optimum braking mode of mine suspended monorail and dependences between the parameters of the rolling stock and the braking force. Obtained dependences allow to establish suitable time to enable or disable the brake of rolling stock, when at initial moment point driving forces still valid, velocity partially quenched, and later – at the moment of shutdown barbell is made additional braking to zero speed. This makes it possible to minimize the deceleration time, increase the efficiency and safety of the mine suspended monorail.

Key words: monorail, rolling stock, dynamic loads, starting, braking.

AUTHORS
Gutarevich V.O., Candidate of Technical Sciences, Assistant Professor,e-mail: gvodonntu@gmail.com
Ignatkina E.L., Assistant, e-mail: sel_post@mail.ru
Donetsk National Technical University, Donetsk, Ukraine.

REFERENCES