Е.Л. Игнаткина

ГОУ ВПО Донецкий национальный техничский университет Донецк

Установлена взаимосвязь между динамическими характеристиками подвесного монорельсового пути и конструкцией подвески для определения выгодного соотношения их параметров, обеспечивающего наилучшие динамические показатели монорельсовой дороги. Найдены эквивалентные коэффициенты жесткости подвески и определены собственные частоты колебаний монорельсового пути.

Ключевые слова: монорельсовый путь, жесткость подвески, собственная частота.

Постановка проблемы Подвесные монорельсовые дороги находят все большее применение в горной промышленности. Их конструкция позволяет перевозить грузы и пассажиров в подвижном составе по подвесному монорельсу, который расположен в верхней части выработки и не занимает полезное рабочее пространство.

Основные преимущества подвесных монорельсовых дорог заключаются в том, что они обеспечивают движение по разветвленным трассам со знакопеременным профилем и углами наклона до 45о. При этом масса подвижного состава достигает 32 т, что позволяет транспортировать крупногабаритное оборудование.

Однако во время эксплуатации подвесной монорельсовой дороги возникают динамические процессы в виде периодических колебаний и ударов, которые воздействуют на крепь горной выработки и уменьшают ее срок службы.

Анализ последних исследований и публикаций В научных исследованиях по рельсовому транспорту [1-3] рассматриваются динамические процессы при движении экипажа по рельсовому пути, методы адаптивного управления, позволяющие автоматически настраивать показатели гашения энергии колебаний. В публикациях [4-6] рассмотрены вопросы применения канатных анкеров для монтажа шахтных подвесных монорельсовых дорог, современные технологии анкерного крепления и проведены расчеты параметров анкеров, служащих для подвешивания монорельсового пути к кровле горной выработки. Работы [7-10] посвящены снижению динамических нагрузок, возникающих во время движения шахтных подвесных монорельсовых дорог.

Анализ приведенных публикаций показывает, что исследования шахтных подвесных дорог не учитывают конструктивные особенности подвески монорельсового пути, а это не позволяет в полной мере использовать ранее полученные результаты. Данная работа является продолжением указанных исследований.

Цель (задачи) исследования

Цель настоящей работы заключается в определении взаимосвязи между динамическими характеристиками подвесного монорельсового пути и конструкцией подвески для установления выгодного соотношения их параметров, обеспечивающего наилучшие динамические показатели монорельсовой дороги.

Для достижения указанной цели необходимо решить следующие задачи: составить расчетную схему подвески пути шахтной монорельсовой дороги; определить эквивалентный коэффициент жесткости и частоты колебаний подвески монорельса; установить взаимосвязь собственных частот монорельсового пути и параметров подвески.

Основной материал исследования

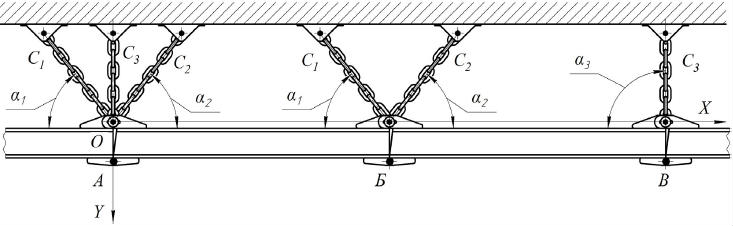
Для определения коэффициента жесткости подвески монорельса, выполненной из нескольких отрезков круглозвенных цепей, составим расчетную схему (рис. 1). На схеме обозначим: α₁, α₂, α₃ - углы установки отрезков цепей; С₁, С₂, С₃ – коэффициенты жесткости соответствующих отрезков цепей и элементов крепления. При составлении расчетной схемы приняты следующие допущения: считаем, что коэффициент жесткости цепи определяет жесткость всего участка; нагрузки, воздействующие на монорельсовый путь, приводят к упругой деформации его подвесок; боковые колебания монорельсового пути ограничены. Здесь вариант А относится к подвеске на трех цепях, вариант Б – на двух цепях, а вариант В – на одной.

Рис.1. Схема подвески пути шахтной монорельсовой дороги.

Рассмотрим деформации δ1, δ2, δ3 соответствующих отрезков цепей, которые происходят при смещении общей точки О (вариант А). Относительно оси x имеем:

δ1 =x cosα₁,

δ2 =-x cosα₂,

δ3 =x cosα₃=0.

Относительно оси y:

δ1 =-y sinα₁,

δ2 =--y sinα₂,

δ3 =-y sin α₃=0.

Уравнения движения вдоль осей x и y:

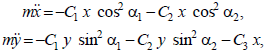
где m – масса монорельсового пути, приходящаяся на один подвес.

На основании этого получим эквивалентные коэффициенты жесткости подвески монорельса относительно соответствующих осей координат:

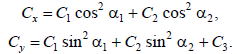
Частоты собственных колебаний подвески монорельса имеют вид:

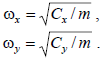
Для крепления монорельсового пути по варианту Б – эквивалентные коэффициенты жесткости подвески монорельса будут:

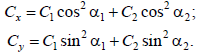
Проведем анализ полученных выражений. На рис. 2а показаны зависимости собственных частот монорельсового пути от параметров подвески стыка монорельса на двух цепях, а на рис. 2б – на трех. Коэффициенты жесткости подвесок, в первом приближении, принимались равными между собой – С_i. Аналогично принимались равными углы α1 и α2–αi.

Из рис. 2а видно, что для подвески на двух цепях с увеличением углов α1 и α2 частота ω_x снижается, а частота ω_y – повышается. Для подвески с коэффициентами жесткости С_i=20000 кН/м при увеличении углов α1 и α2 от 0,1 до 1 рад частота колебаний ωx уменьшается от 100 до 55 с-1, а частота ω_y – увеличивается до 84 с-1. Если уменьшить значения коэффициентов жесткости подвески до 2000 кН/м, то при таком же изменении углов _x – уменьшается с 32 до 18 с-1, а ω_y – увеличивается до 28 с-1. Однако, в зависимости от жесткости подвески, показатели частоты _x значительно отличаются, то есть при Сi=20000 кН/м _x понижается от 100 до 55 с-1, а при Сi=2000 кН/м – от 32 до 18 с-1, что составляет 57% при αi=0,1 рад и 31% при αi= 1 рад. При коэффициенте жесткости С_i=20000 кН/м и αi=0,8 рад значения частоты ω_y в 1,5 раза ниже при подвешивании монорельсового пути на двух подвесках, чем ее же значения при использовании трех подвесок. Показатели частоты ωx уменьшаются в 3 раза при снижении коэффициента жесткости от 20000 до 2000 кН/м.

Аналогичное изменение частот происходит при использовании подвески на трех цепях (рис. 2б), где частота ωx снижается абсолютно идентично подвеске, состоящей из двух цепей, а частота ω_y – повышается, но с другими значениями: при С_i=20000 кН/м повышается на 35%, а если для подвески использовать материал с жесткостью 2000 кН/м, то ω_y изменится всего лишь на 12%.

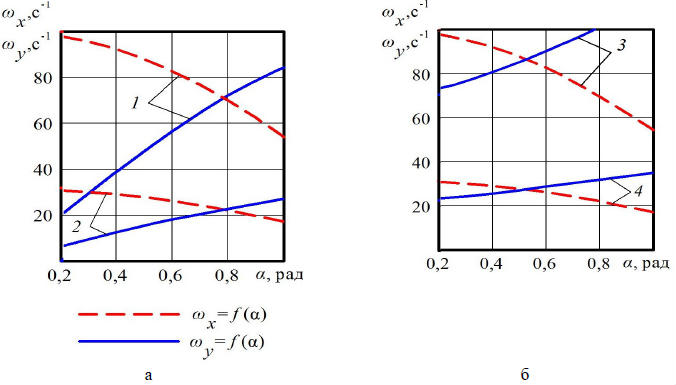
Рис.2. Графические зависимости собственных частот монорельсового пути от параметров подвески: a – на двух цепях; б – на трех цепях; 1, 3 – С_i=20000 кН/м; 2, 4 – С_i=2000 кН/м

Выводы

На основании проведенных исследований определены зависимости эквивалентных коэффициентов жесткости подвески монорельсового пути от способа его крепления в горной выработке. Это позволило найти значения частот собственных колебаний монорельсового пути, которые составляют от 22 до 100 с-1. Анализ результатов показал, что при коэффициенте жесткости С_i=20000 кН/м и α_i=0,8 рад значения частоты в 1,5 раза ниже при подвешивании монорельсового пути на двух подвесках, чем ее же значения при использовании трех подвесок. Установленная взаимосвязь собственных частот монорельсового пути и параметров подвески позволяет обоснованно находить собственные частоты колебаний отдельных элементов подвесной монорельсовой дороги и моделировать динамические процессы, возникающие во время ее движения для определения выгодного соотношения параметров.

Список литературы

1. Математическое моделирование колебаний рельсовых транспортных средств / В.Ф. Ушкалов [и др.]. – К.: Наукова думка, 1989. – 240 с.
2. Говоруха В.В. Механика взаимодействия рельсового пути, подвижных транспортных средств и смежных устройств: монография. – Донецк: Лира, 2006. – 448 с.
3. Шахтарь П.С. Рудничные локомотивы. – М.: Недра, 1982. – 296 с.
4. Еременко В.А. Современные технологии анкерного крепления / В.А. Еременко, Е.А., Разумов, Д.Ф. Заятдинов // Горный информационно-аналитический бюллетень. – М.:Горная книга. - 2012. –№12. – С. 38-45.
5. Применение канатных анкеров для монтажа монорельсовых подвесных дорог / П.В. Гре- чишкин [и др.] // Уголь Украины. – 2013. – №4. – С. 25-26.
6. Хлусов А.Е. К расчету параметров анкеров, служащих для подвешивания монорельсовой дороги к кровле горной выработки / Сб. науч. тр. ВНИМИ / под ред. Д.В. Яковлева. – СПб.: ВНИМИ, 2012. – С. 317-322.
7. Гутаревич В.О. Динамика шахтных подвесных монорельсовых дорог: монография. – Донецк: ЛАНДОН-ХХІ, 2014. – 206 с.
8. Гутаревич В.О. Динамическая нагруженность монорельсовых тележек и подвесного пути / Известия вузов. Северо-Кавказский регион. Технические науки. – 2015. – №4. – C. 85-88.
9. Gutarevych V.O. Mathematical modeling of end carriage motion on the overhead monorail / Metallurgical and Mining Industry. – 2014. – No.5. – P. 51-55.
10. Gutarevych V. Dynamic model of the movement of mine suspended monorail / Transport Problems. – 2014. – Vol.9, Issue 1. – Р. 13-19.

Е.L. Ignatkina

Donetsk National Technical University (Donetsk)

The dynamic characteristics of mine suspended monorail

Background. During the operation of mine suspended monorail arise the dynamic processes in the form of periodic oscillations and bumps, which affect its elements and mine workings support, and reduce their service life. The reduction of these periodic oscillations and bumps is a topical scientific and technical problem.
Materials and/or methods. The objective of this paper is to determine the relationship between the dynamic characteristics of the suspended monorail and the suspension design to establish a favorable proportion of their parameters that ensure the best overall dynamic performance of the monorail. For this purpose, the following tasks solved: a design scheme of spatial suspension of the mine monorail created; equivalent factors of stiffness and frequency of the monorail suspension oscillations defined; the correlation of eigenfrequencies of a monorail and suspension parameters established.
Results. The methodology for determining equivalent stiffness factors of a spatial suspension monorail in mine workings proposed. The options of the joints suspension of a monorail on two and three chains as well as on one chain considered. The dependencies of equivalent stiffness factors of the monorail suspension on its fixation method in mine workings obtained. Based on this, the values of the eigenfrequencies of a monorail obtained, which are from 22 to 100 s-1. Analysis studies have shown that the lowest values of the oscillation eigenfrequencies of a monorail track can be obtained for suspension with three chains, each having a stiffness factor 2000 kN/m. Conclusion. Established interrelation of eigenfrequencies of a monorail and the parameters of suspension allows finding the eigenfrequencies of the individual elements of a suspended monorail and simulate dynamic processes that occur during its movement, to determine a favorable proportion of the parameters that provide the best dynamic performance of the monorail.

Keywords: monorail, suspension stiffness, eigenfrequency.