В.О. Гутаревич /к.т.н./, В.П. Кондрахин /д.т.н./

ГОУ ВПО Донецкий национальный техничский университет Донецк

Разработана математическая модель, описывающая колебательные процессы, возникающие во время движения подвижного состава по стыкам подвесного монорельсового пути. Установлены оптимальные параметры подвески монорельса, позволяющие снизить динамические нагрузки на крепь горной выработки. Предложено устройство для снижения динамических на грузок в подвеске монорельса.

Ключевые слова:горная выработка, монорельсовый путь, подвижной состав, подвеска, динамические нагрузки.

Постановка проблемы Эксплуатация шахтных подвесных монорельсовых дорог неизбежно связана с дополнительными нагрузками, действующими на крепь горных выработок. Во время движения подвижного состава по подвесному монорельсу, кроме статических сил, к верхнякам крепи передаются и динамические силы. Эти силы приводят к колебаниям подвижного состава, монорельсового пути, а также крепи. Колебания крепи вызывают смещения горных пород, что снижает их устойчивость и приводит к уменьшению поперечного сечения выработок. В результате повышается аварийность, снижается эффективность и безопасность работы шахтных подвесных монорельсовых дорог. Поэтому для горных предприятий проблема снижения динамических нагрузок на монорельсовый путь и крепь является актуальной.

Анализ последних исследований и публикаций Вопросы повышения эффективности подвесных монорельсовых дорог при подготовке запасов угля к очистной выемке рассмотрены в работах [1-2]. Авторами предложены ресурсосберегающие технологические схемы комплексного использования адаптивных возможностей подвесных дизельных монорельсовых дорог для интенсификации подготовительных работ, повышения темпов подготовки и отработки выемочных столбов при разработке тонких угольных пластов. Исследования [3-7] посвящены современным технологиям подвешивания монорельсовой дороги к кровле горной выработки и обоснованию параметров анкеров. Установлено, что их применение позволяет снизить материалоемкость крепи, сроки монтажа и трудоемкость транспортных работ. Динамические процессы, возникающие во время эксплуатации шахтной подвесной монорельсовой дороги, рассмотрены в работах [8-9]. Данная статья является продолжением указанных исследований.

Цель (задачи) исследования

Цель настоящей работы заключается в оптимизации параметров монорельсового пути и подвижного состава для установления выгодного их соотношения, обеспечивающего наилучшие динамические характеристики шахтной подвесной монорельсовой дороги.

Для реализации указанной цели решены следующие задачи: составлена расчетная схема воздействия подвижного состава на подвеску монорельсового пути; разработана математическая модель, описывающая колебательные процессы, возникающие во время движения подвижного состава по стыкам монорельса; установлены критерии оптимизации и определены оптимальные параметры подвески монорельсового пути, позволяющие снизить динамические воздействия на крепь горной выработки. При решении указанных задач принимались следующие допущения: боковое раскачивание монорельса исключалось за счет применения растяжек; контакт колес ходовых тележек с монорельсом считался постоянным, скорость движения подвижного состава V_n принималась постоянной.

Основной материал исследования

Рассмотрим процесс воздействия на крепь горной выработки динамических нагрузок, возникающих во время движения подвижного состава по стыкам монорельсового пути в местах их подвески. Расчетная схема динамического воздействия подвижного состава на подвеску монорельсового пути показана на рис. 1. На схеме обозначено: m₁, m₂ - массы монорельса и подвижной единицы состава, приходящиеся на одну подвеску монорельсового пути, соответственно; z₁, z₂ - координаты центров тяжести масс m₁ и m₂, соответственно; m₁, C_p1, β_p1 - соответственно коэффициенты жесткости и вязкого трения подвески монорельсового пути; C_p1, β_p1 - аналогично коэффициенты жесткости и вязкого трения ходовой тележки; η(t) - возмущения от монорельсового пути, воздействующие на ходовую тележку подвижного состава.

Рис. 1. Расчетная схема динамического воздействия подвижного состава на подвеску монорельсового пути: 1 - кровля горной выработки; 2 - подвеска монорельса; 3 -монорельсовый путь; 4 - подвижной состав

При движении подвижного состава по стыку монорельсового пути возмущения η(t), воздействующие на массу m₂, могут быть представлены в виде одиночной неровности, повторяющейся периодически:

где η_0S, η_10S -высота и длина неровности, образуемой при движении ходовой тележки по стыку монорельсового пути, соответственно; x - пройденный путь за время t.

Подобный вид возмущений широко используется при исследовании взаимодействия колеса с рельсовыми стыками для железнодорожного транспорта [10-11] и довольно точно соответствует стыкам (соединениям) секций монорельса. Как функция пройденного пути x=V_nt указанная неровность для одиночного стыка монорельса (при η_0S=0,005 м, η_10S=0,3 м) представлена на рис. 2.

Под воздействием на массу m2 возмущений η(t) за счет деформации подвески возникают колебания и динамические силы, передающиеся на подвижной состав, а также крепь горной выработки. Согласно расчетной схеме, приведенной на рис. 1, указанные колебания описываются следующими уравнениями:

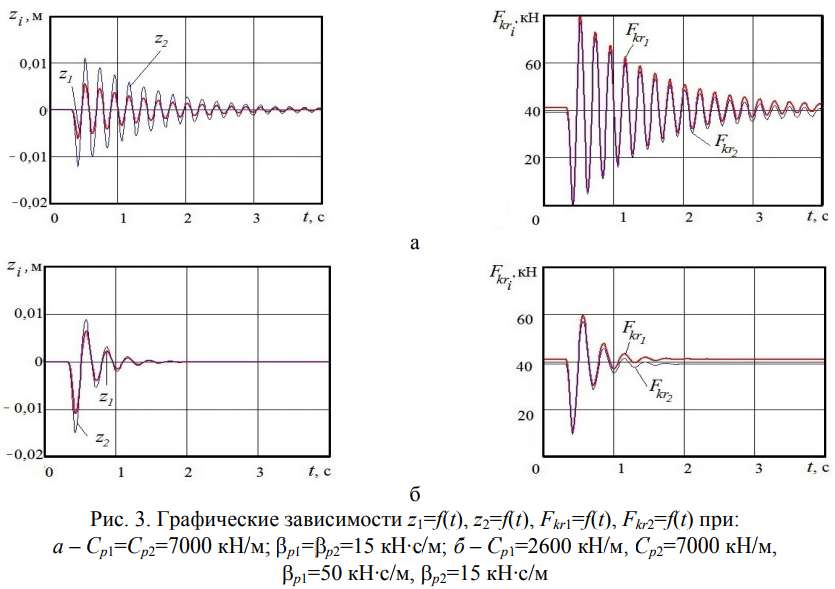
Графические зависимости амплитуд смещений z₁ и z₂, полученные на основании решения этих уравнений, представлены на рис. 3. При этом принимали значения входящих параметров, характерные для большинства современных шахтных подвесных монорельсовых дорог: m₁=0,2 т; m₁=4 т; η_0S=0,005 м, η_10S=0,3 м и V_n=3 м/с. Усилие в подвеске монорельсового пути F_kr1 и усилие в подвеске ходовой тележки F_kr2 находили следующим образом:

Из рис. 3 видно, что для разных значений параметров подвеса колебания происходят с различными амплитудами, частотами, также темпами затухания. Если C_p1=C_p2=7000 кН/м и η_p1=η_p2=15 кН·с/м (рис. 3а), то по абсолютной величине z₁ достигает до 6,1 мм, а z₂ - до 12 мм. Кроме того, наибольшее усилие в подвесе F_kr1 составляет 80,2 кН, а усилие в подвеске тележки F_kr2 принимает значение - 77,3 кН. Как показано на рис. 3б, при C_p1=2600 кН/м и C_p2=7000 кН/м, η_p1=50 кН·с/м и η_p2=15 кН·с/м имеем наибольшее значение z₁ - 12 мм, а z₂ - 17 мм. При этом наибольшие усилия соответственно составляют - 59,6 и 57 кН. В последнем случае наибольшие нагрузки F_kr1 снижаются более чем в 1,35 раза.

Рис. 2. Возмущения от неровности, образуемой во время движения ходовой тележки по стыку секций монорельса: x - пройденный путь: 1 - вертикальные возмущения; 2 - производная от вертикальных возмущений

Следовательно, изменяя значения C_p1, C_p2 и η_p1, η_p2, возможно управлять динамическими нагрузками, воздействующими на подвес монорельсового пути, а также крепь горной выработки. Значения этих параметров, при которых F_kr1 принимает минимальное значение, следует считать оптимальным, при этом вертикальные перемещения, возникающие в подвеске, должны не превышать допускаемых значений f_доп.

В качестве критериев (функций цели) оптимальности следует принять динамические нагрузки в подвеске монорельсового пути, а также вертикальные перемещения, которые возникают во время движения подвижного состава.

В общем случае математическую модель оптимизации параметров подвеса монорельсового пути можно записать в виде:

где X_опт - вектор параметров подвеса монорельсового пути, соответствующий оптимальному значению целевой функции F_kr1=F(X,C); X - вектор параметров подвеса; C - вектор констант, не зависящих от параметров подвеса; f_δi - деформация подвеса под воздействием статических и динамических сил, которые возникают во время движения подвижного состава по монорельсу: f_δi=z₁+δ₁, где δ₁ - деформация подвески от нагрузки (m₁+m₂)g, прикладываемой статически, равная δ₁=(m₁+m₂)g/C_p1.

Согласно нормативным документам для шахтных подвесных монорельсовых дорог прогиб пути должен быть f_δi≤L_s/200, где L_s - длина секции монорельсового пути. Для стандартной секции длиной L_s=3 м прогиб составляет 15 мм, поэтому указанное значение принимаем в качестве ограничения деформации монорельсового пути в месте его подвески и учитываем при проведении оптимизации параметров.

Оптимизацию динамических процессов проводили методом последовательных приближений. При этом на каждом последующем приближении определяли обобщенный критерий и находили значения оптимизируемых параметров, обеспечивающих минимальное значение критерия.

На основании результатов проведенной оптимизации подвеса монорельсового пути и ходовой тележки получены следующие значения: C_p1=5060 кН/м; C_p2=4070 кН/м; β_p1=β_p2=50 кН·с/м. При этом наибольшая нагрузка на подвес составляет F_kr1=54,2 кН. Таким образом, применение подвеса с демпфирующим устройством, имеющим оптимальные параметры, позволяет снизить динамические нагрузки более чем в 1,5 раза. Проведенные исследования позволили разработать способ подвески монорельсового пути в горной выработке (патенты UA109446C2 от 27.08.2013, UA110136С2 от 25.11.2015). Общий вид подвеса, позволяющего реализовать указанный способ и установленные параметры, приведен на рис. 4.

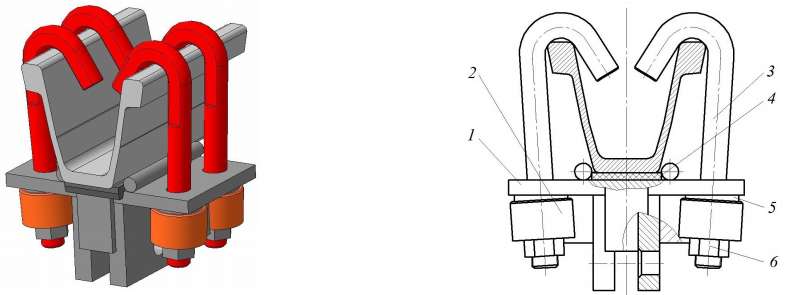
Рис. 4. Общий вид (слева) и конструкция (справа) подвеса для монорельсового пути: 1 - корпус; 2 - упругодемпфирующее устройство; 3 - крепежный болт; 4 - амортизирующая вставка (прокладка); 5 - косая шайба; 6 - гайка

Подвес закрепляется к арочной крепи и служит опорой для подвесного монорельсового пути. В его состав входят тарельчатые пружины и плоские шайбы, располагаемые во втулке и фиксируемые стопорным кольцом. Втулки присоединяются к нижней части корпуса подвеса, который прикрепляется к верхняку арочной крепи крепежными болтами или хомутами. К проушинам подвеса с помощью пальца со шплинтом присоединяется круглозвенная цепь, поддерживающая монорельсовый путь. При этом между корпусом и профилем крепи располагаются амортизирующая вставка из податливого материала и металлический ограничитель сжатия высотой, равной половине толщины вставки в недеформируемом состоянии.

Таким образом, возникающие во время эксплуатации подвесной монорельсовой дороги вертикальные колебания пути воспринимают тарельчатые пружины и амортизирующие вставки, которые обеспечивают энергопоглощение ударов и гашение периодических колебаний.

Выводы

На основании проведенных исследований можно сделать следующие выводы.

1. Разработана математическая модель вертикальных колебаний монорельсовой дороги, которая позволяет установить взаимосвязь между параметрами подвижного состава и динамическими нагрузками, действующими в подвеске. В результате получены значения деформации монорельсового пути и определены динамические нагрузки, воздействующие на крепь горной выработки. работки.
2. Выбраны критерии оптимальности и разработана математическая модель оптимизации параметров подвеса монорельсового пути. Для условий, характерных для большинства современных шахтных подвесных монорельсовых дорог, установлено, что при коэффициентах жесткости подвески монорельсового пути 5060 кН/м, ходовой тележки подвижного состава 4070 кН/м, а также их коэффициенте вязкого трения 50 кН·с/м динамические нагрузки на крепь горной выработки принимают минимальные значения.
3. Предложено устройство для монорельсо- вого пути, позволяющее уменьшить указанные нагрузки более чем 1,5 раза, что дает возможность повысить устойчивость горных выработок, эффективность и безопасность работы шахтных подвесных монорельсовых дорог.

   Список литературы

   1. Ширин Л.Н. Повышение эффективности работы монорельсовых дорог при подготовке запасов угля к очистной выемке: монография / Л.Н. Ширин, В.А. Расцветаев, А.И. Коваль – Днепропетровск: НГУ, 2014. – 144 с.
   2. Расцветаев В.А. Дополнительные нагрузки от действия подвесных монорельсовых дорог на арочное крепление выработок в условиях шахт Западного Донбасса // Геотехническая механика. – 2014. – №117. – С. 53-59.
   3. Ногих В.Р. Взаимодействие подвесных транспортных средств с породами и обеспе- чение безопасности и устойчивости горных выработок // Известия ТулГУ. Науки о Зем- ле. – 2015. – Вып.4. – С. 65-75.
   4. Применение канатных анкеров для монтажа монорельсовых подвесных дорог / П.В. Гре- чишкин [и др.] // Уголь Украины. – 2013. – №4. – С. 25-26.
   5. Chanda E.K. A computer simulation model of a monorail-based mining system for decline development / E.K. Chanda, B. Besa // International Journal of Mining, Reclamation and Environment. – 2011. – Vol.25, Issue 1. – Р. 52-68.
   6. Grujic M. Difficulties with transportation of long and heavy supplies in coal mines / M. Grujic, D. Kuzmanovic // Journal Transport and Logistic. – 2002. – Vol.3, Issue 5. – Р. 27-33.
   7. Tokarczyk J. Migration of computational models in the virtual prototyping of complex mechanical systems // Proceeding of the World Congress on Engineering and Computer Science. – 2012. – Vol.II. – Р. 1334-1337.
   8. Гутаревич В.О. Динамика шахтных подвес- ных монорельсовых дорог: монография. – Донецк: ЛАНДОН-ХХІ, 2014. – 206 с.
   9. Gutarevych V. Dynamic model of the movement of mine suspended monorail // Transport Problems. – 2014. – Vol.9, Issue 1. – Р. 13-19.
   10. Математическое моделирование колебаний рельсовых транспортных средств / В.Ф. Уш- калов [и др.]. – К.: Наукова думка, 1989. – 240 с.
   11. Говоруха В.В. Механика взаимодействия рельсового пути, подвижных транспортных средств и смежных устройств: монография. – Донецк: Лира, 2006. – 448 с.

   V.O. Gutarevych /Cand. Sci. (Eng.)/, V.P. Kondrakhin /Dr. Sci. (Eng.)/

   Donetsk National Technical University (Donetsk)

   Reduction of dynamic loads from suspended monorailL tracks on mine workink supors

   Background. During the rolling stock movement on a suspended monorail, in addition to the static gravity forces of these elements of roads, dynamic forces are transmitted to the mine working support. These forces cause the displacement of rocks, which lowers their stability and leads to the reduction of the cross section of workings. The result is increased accidents, reduced efficiency, and safety of suspended monorail tracks. Therefore, for mining companies the problem of reducing dynamic loads on the monorail track and the support is relevant.
   Materials and/or methods. The objective of this paper is to optimize parameters of the monorail track and rolling stock to establish proportions that provide the best dynamic performance of a suspended monorail track. For this purpose, the following tasks solved: a design scheme of dynamic effects of rolling stock on the monorail track suspension and mining supports created; a mathematical model describing oscillatory processes arising during rolling stock movement on the joints of the monorail developed; the optimization criteria were chosen and optimal parameters of the monorail track suspension defined, allowing to reduce the dynamic effects on mine working support.
   Results. The mathematical model of optimization of parameters of a monorail track suspension developed. It is found that, for conditions typical of the majority of mine suspended monorail tracks, with the stiffness coefficient of a suspended monorail track 5060 kN/m, the undercarriage of the rolling stock 4070 kN/m, and their coefficient of viscous friction 50 kN·s/m, dynamic loading on the mine working support has the minimum value. The device for a monorail track allowing reduction of these loads more than 1.5 times proposed.
   Conclusion.The obtained results will allow establishing parameters of a monorail track, reducing the dynamic loads from rolling stock on mining supports, increasing the stability of mine workings, efficiency and safety of mine suspended monorail tracks.

   Keywords: : mine working, monorail track, rolling stock, suspension, dynamic loads.