Определение октанового числа из спектроскопических данных
Во многих приложениях необходимо определить нехимические параметры из данных спектроскопии. Это часто считается проблемой, поскольку спектроскопические методы были разработаны для отражения химических изменений в образцах, где поиск уникальной пиковой информации для отделения одного компонента от другого. Многомерный метод PLS-регрессии очень эффективен при извлечении информации о дисперсии из сложных, по-видимому, диффузных данных, которые мы можем использовать для связи октанового числа в образцах бензина с поглощением света в ближнем инфракрасном диапазоне длин волн.
Следующее приложение демонстрирует, как UOP / Guided Wave Inc успешно применяет многомерные методы калибровки для оценки октанового числа продуктов нефтепереработки из спектральных данных ближнего инфракрасного диапазона. Это приложение высоко освещает методы, сделанные с помощью многомерного программного пакета Unscrambler для разработки калибровочных моделей для лаборатории и он-лайн. Данные, приведенные ниже, были использованы в технико-экономическом обосновании для одного из их клиентов нефтехимической промышленности, где требуется контроль октанового числа. Заявка также важна для регулирующих органов, ответственных за проверку октанового числа в коммерческих учреждениях. Использование анализа NIR в сочетании с многовариантной калибровкой и прогнозированием обеспечивает большую экономию времени по сравнению с традиционной методологией для этого анализа.
1. Проблема
Сделайте модель, которая предсказывает октановое число из спектроскопических данных. В спектрах нет селективных длин волн, поэтому одномерная регрессия невозможна (см. Раздел 4).
2. Входные данные
Для создания модели мы подготовили набор обучающих данных (набор калибровки): для каждого из 26 репрезентативных образцов (объектов) бензина, которые, как считается, охватывают важные вариации, мы зафиксировали спектры поглощения NIR на 226 длинах волн (X-переменные нет 1 - 226) и октановое число (Y-переменная). Они хранятся в матрицах XTrain и YTrain. Чтобы предсказать (оценить, определить) октановое число в новых образцах, мы имеем 14 образцов бензина с показаниями оптической плотности (226 длин волн), но с неизвестным октановым числом. Они хранятся в матрице XNew. Мы будем использовать модель для прогнозирования октановых чисел этих образцов.
3. Необработанные данные
Мы используем программный пакет Unscrambler для многовариантного анализа и графического представления. Используя графический объект Matrix, построим XTrain, мы можем изучить спектры для всех образцов. Масштабирование показывает, что самый чистый пик составляет 1194 нм.
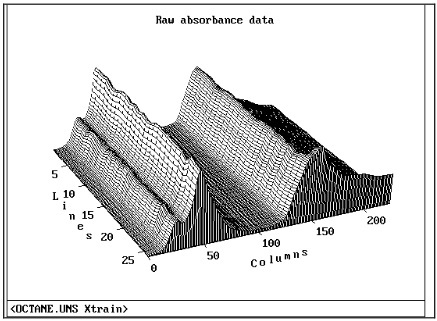
Рис. 1 Спектр поглощения необработанных данных для 26 образцов бензина
4. Однократная регрессия
Общий 2-векторный график позволяет нам попробовать одномерную регрессию, построив самый ясный пик поглощения (X48 = 1194 нм) по сравнению с измеренным октановым числом (Y). Регрессия вовсе не подходит для прогнозирования.
5. Многомерная регрессия
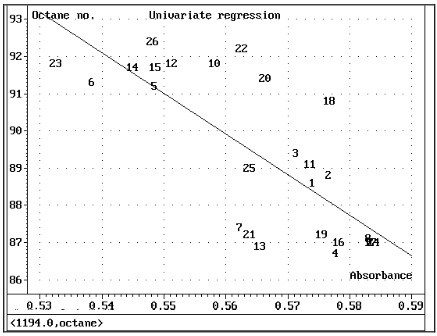
Рис. 2 Одномерная регрессия дает плохое предсказание, хотя мы используем самый чистый пик.
Мы читаем набор данных обучения в программу. В меню «Модель» мы выбираем метод регрессии и параметры модели. Мы выбираем PLS (Частичные наименьшие квадраты, поскольку информация в Y-переменных важна для разложения X-матрицы) и быстрый метод проверки - коррекция плеча - для создания первой модели. Экран калибровки (ниже) дает обзор сгенерированной модели; выбросы и ошибка прогнозирования (остаточная дисперсия) после каждого компонента PLS (ПК) (см. также раздел 7):
+-------------------+ ¦Mo+----------------------------------------------------------+----------+ ¦St¦ # ¦ Warnings ¦ Validation variance ¦ ¦ ¦Ch¦ PC ¦ Outl. Lev. ¦ Y(Res) ¦ ¦ ¦Re¦ 0 ¦ 10 ¦ 4.571 ¦##############################¦ 4.000 ¦ ¦Na¦ 1 ¦ 00 ¦ 5.826 ¦##############################¦ 0.900 ¦ ¦Co¦ 2 ¦ 80 ¦ 0.660 ¦#### ¦ 1 ¦ ¦Ca¦ 3 ¦ 10 ¦ 0.104 ¦# ¦ ¦ +--¦ 4 ¦ 10 ¦ 0.117 ¦# ¦ tion ¦ ¦ ¦----------+ +----------------------------------------------------------+
Мы также получаем обзор модели; имена, комментарии, наборы данных и параметры модели, оптимальное количество ПК и т. д. При сканировании каталога для моделей эта информация доступна, чтобы помочь нам отслеживать все модели и файлы данных.
+-------------------+
¦Model parameter+--------------------------------------------------------+
¦Storage paramet¦Calibration date: Sept 18 1991 ¦
¦Change weights ¦X-matrix: Xtrain octane.UNS ¦
¦Remove objects ¦Y-matrix: Ytrain octane.UNS ¦
¦Name ¦Calibration met. PLS1 with Y-var. octane ¦
¦Comments ¦Validation met. Leverage correction ¦
¦Calibrate ¦ +--------------------------------------¦
+---------------¦ 226 X-var. ¦ Raw data ¦
¦1 Y-var. ¦ ¦
¦26 Objects ¦ ¦
¦0 removed ¦ ¦
¦ ¦ ¦
¦4 PCs ¦ ¦
¦3 is optimal ¦ ¦
+-------- List info Warnings Rem.obj. Variance -------+
X-matrix: octane.UNS Xtrain (26,226) Model: test 1
Y-matrix: octane.UNS Ytrain (26,1) 350000
Обзор модели
Экран калибровочного выхода выше указанных предупреждений о выбросах в нескольких вычислительных компьютерах, то есть предупреждения для образцов (объектов) и / или переменных, которые могут быть ненормальными. Через меню в обзоре модели (выше) мы получаем подробный список предупреждений:
+-------------------+
¦Model parameter+---+--------------------------------------------+-------+
¦Storage paramet¦Cal¦ ¦ ¦ ¦ ¦Outlier¦Leverage¦ ¦
¦Change weights ¦X-m¦PC ¦ Test ¦ Obj ¦ Var ¦ 4.000 ¦ 0.900 ¦ ¦
¦Remove objects ¦Y-m¦0 ¦X-variance ¦ 26 ¦ ¦ 4.110 ¦ ¦ ¦
¦Name ¦Cal¦2 ¦X-data ¦ 25 ¦ 154 ¦ 4.174 ¦ ¦ ¦
¦Comments ¦Val¦2 ¦X-data ¦ 25 ¦ 155 ¦ 4.447 ¦ ¦ ¦
¦Calibrate ¦ ¦2 ¦X-data ¦ 25 ¦ 156 ¦ 4.406 ¦ ¦-------¦
+---------------¦ 2¦2 ¦X-data ¦ 25 ¦ 157 ¦ 4.086 ¦ ¦ ¦
¦ ¦2 ¦X-data ¦ 26 ¦ 154 ¦ 4.198 ¦ ¦ ¦
¦ ¦2 ¦X-data ¦ 26 ¦ 155 ¦ 4.426 ¦ ¦ ¦
¦ ¦2 ¦X-data ¦ 26 ¦ 156 ¦ 4.357 ¦ ¦ ¦
¦ ¦2 ¦X-data ¦ 26 ¦ 157 ¦ 4.027 ¦ ¦ ¦
¦ ¦3 ¦X-data ¦ 17 ¦ 155 ¦ 4.057 ¦ ¦ ¦
¦ ¦4 ¦X-data ¦ 14 ¦ 155 ¦ 4.063 ¦ ¦ ¦
+---¦ ¦-------+
+------------- ↑↑↑↑ ↓↓↓↓ PgUp PgDn-------------+
Предупреждения от калибровочной модели OCT ver 0
Список показывает, что объекты 25 и 26 постоянно указываются как выбросы (а также нет 17, 14 на последующих ПК).
6. Графическое исследование выбросов
Давайте подробнее рассмотрим объекты! Мы покидаем меню «Модель», открываем меню «График» и выбираем график «Оценка», который показывает проекционные местоположения объектов на основные компоненты, т.е. какие образцы влияют на модель и как?
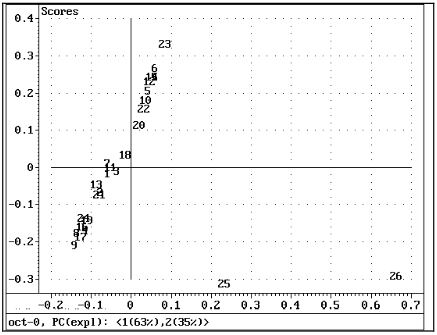
Рис. 3 Оценки для ПК 1 по сравнению с ПК 2
Объекты, расположенные далеко от начала координат, оказывают наибольшее влияние на модель. При построении графика для ПК 1 и ПК 2 мы видим, что объекты, не содержащие 25 и 26, помещаются в группу отдельно от других. Они также сильно влияют на модель (поскольку они имеют высокие значения оценки в ПК 1 (который моделирует большинство общих вариаций). Как показано в нижней части графика, два первых ПК описывают 63% + 35% = 98% общая X-дисперсия.
Кажется разумным полагать, что объекты 25 и 26 действительно являются выбросами - аномальные образцы, которые приводят к смещению модели и делают ее бесполезной для прогнозирования. Совершенно очевидно, что Unscrambler обнаружил ошибки в этих двух образцах, и если вы внимательно посмотрите на матричный график (рис.1), вы можете обнаружить, что спектры для этих выборок немного отклоняются от остальных. Исходные образцы на самом деле содержат алкоголь.
7. Повторная калибровка с удалением
Теперь мы выполним новую калибровку с объектами № 25 и 26, удаленными из калибровочного набора. Вернемся к меню модели, где мы можем отметить, что эти объекты должны храниться вне калибровки. Мы также меняем метод проверки на более консервативную проверку Cross. Затем мы начнем новый калибровочный прогон.
На экране калибровочного экрана (ниже) теперь нет предупреждений о выбросах. Строки # -значений указывают на ошибку предсказания (остаточная дисперсия) после каждого ПК. Даны их численные значения. На этот раз мы также получаем меньше ПК; два первых ПК описывают большинство полных вариаций в Y. Отклонения легче изучаются с использованием готовых графиков зависимости.
+-------------------+ ¦Mo+----------------------------------------------------------+----------+ ¦St¦ # ¦ Warnings ¦ Square error of prediction ¦ ¦ ¦Ch¦PC ¦ Outl. Lev. ¦ Y ¦ ¦ ¦Re¦0 ¦ 00 ¦ 4.747 ¦##############################¦ 4.000 ¦ ¦Na¦1 ¦ 00 ¦ 0.781 ¦##### ¦ 0.900 ¦ ¦Co¦2 ¦ 00 ¦ 0.104 ¦# ¦ 1 ¦ ¦Ca¦3 ¦ 00 ¦ 0.81E-01¦# ¦ ¦ +--¦4 ¦ 00 ¦ 0.66E-01¦ ¦ n ¦ ¦ ¦----------+ +----------------------------------------------------------+
Тем не менее, легче изучить результаты графически, поэтому перейдем в меню «График» еще раз.
8. Интерпретация калибровочной модели
Отклонение
Давайте сначала рассмотрим график Variance, который показывает, насколько хорошо модель описывает изменения в данных. Мы можем изучить дисперсию как дисперсию объяснения или остаточную дисперсию для X-переменных или Y-переменных. Ниже приведено объяснение дисперсии для Y-переменной (число Октана).
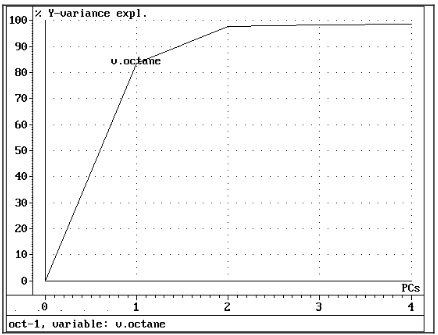
Рис. 4 Разъясненная дисперсия. Два ПК описывают 98% всех вариаций Y.
На основе этого графика мы выбираем, сколько ПК должно быть включено в модель. Как правило, мы ищем количество ПК, которые минимизируют остаточную дисперсию (максимизирует дополнительную объясненную дисперсию), но не принимая больше, чем абсолютно необходимо, чтобы гарантировать, что мы не переоцениваем (модельный шум). Два компьютера объясняют 98%, а три компьютера объясняют 99%.
Результаты
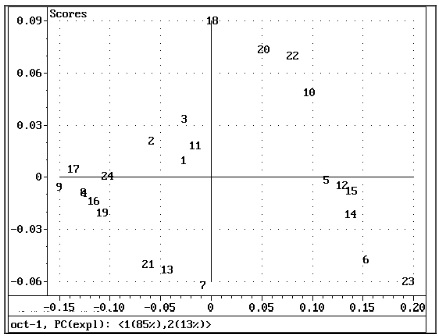
Рис. 5 Комбинация ПК 1 и ПК 2 описывает изменение в образцах, рассматриваемых как подгруппы (окруженные вручную).
При построении оценок для двух первых ПК мы не видим очевидных выбросов. Однако мы видим подгруппы. Изучая образцы и их характеристики, мы можем интерпретировать смысл основных компонентов. Кажется, например, что объекты 1-2-3-11 имеют что-то общее. Мы можем идентифицировать эти группы в зависимости от их типа бензина. (Называя объекты интеллектуальным способом, например, отражая их состав или происхождение, мы можем иногда видеть шаблоны более легко, так как программа позволяет нам при необходимости называть имена вместо чисел.)
Способность предсказания
График Pred / meas (здесь с 3 ПК) показывает соответствие между известными октановыми числами и октановым числом, как это предсказывает модель. Мы видим здесь те же подгруппы, что и в сюжете Score! Группы представляют образцы с тем же октановым числом. Мы также можем записать предсказанные и измеренные с использованием двух моделей ПК. Это дает более низкую корреляцию, 0,995, почему эта модель имеет несколько худшую способность предсказания.
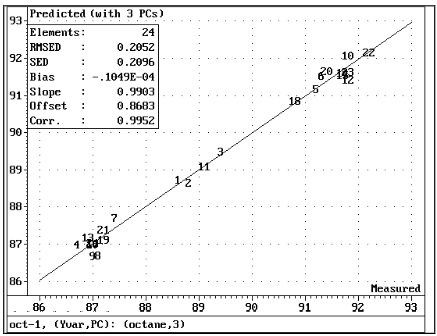
Рис. 6 Прогнозируемые значения измеренных октановых чисел с помощью модели с тремя ПК. Хорошая корреляция: 0,995.
9. Как прогнозировать новые образцы?
Теперь мы можем прочитать новый набор данных XNew, содержащий только показания поглощения для 14 новых образцов бензина. Затем мы открываем меню Predict, вводим имя используемой модели; OCT версии 1 и сколько ПК использовать; 3. Прогнозирование происходит сразу, а информация о прогоне прогнозирования и числовые значения прогнозируемого октанового числа отображаются в окне.
+-+------------- Y-predicted -------+------------------+ ¦ ¦ Object octane Deviation ¦ Aug 09 1991 ¦ ¦ ¦S.003 88.855 0.150 ¦ octane.UNS ¦ ¦ ¦S.004 88.933 0.113 ¦PCs ¦ ¦ ¦S.010 91.064 0.273 ¦ne ¦ ¦ ¦S.016 91.902 0.158 ¦y selected ¦ ¦ ¦S.019 88.907 0.158 ¦------------------¦ ¦ ¦S.022 90.727 0.163 ¦ ¦ ¦ ¦S.025 88.708 0.118 ¦ ¦ ¦ ¦S.026 91.398 0.212 ¦ ¦ ¦ ¦S.034 87.154 0.257 ¦ ¦ ¦ ¦S.055 97.769 7.390 ¦ ¦ ¦ ¦S.056 96.169 7.312 ¦ ¦ ¦ ¦S.057 98.692 8.854 ¦ ¦ +-¦S.058 97.132 7.656 ¦dicted -----------+ +---------------------------------+
Мы также получаем предупреждения об исключениях для объектов 11, 12, 13 и 14.
+---------------------------------------------+ ¦ ¦ ¦ ¦ ¦Outlier¦Leverage¦ ¦ Fac¦ Test ¦ Obj¦ Var¦ 5.000 ¦ 0.900 ¦ ¦3 ¦ X-variance ¦ 10 ¦ ¦ 39.194¦ ¦ ¦3 ¦ X-variance ¦ 11 ¦ ¦ 38.791¦ ¦ ¦3 ¦ X-variance ¦ 12 ¦ ¦ 46.905¦ ¦ ¦3 ¦ X-variance ¦ 13 ¦ ¦ 40.613¦ ¦ ¦3 ¦ Object ¦ 10 ¦ ¦ ¦ 52.910 ¦ ¦3 ¦ Object ¦ 11 ¦ ¦ ¦ 51.182 ¦ ¦3 ¦ Object ¦ 12 ¦ ¦ ¦ 80.198 ¦ ¦3 ¦ Object ¦ 13 ¦ ¦ ¦ 56.218 ¦ +---------------------------------------------+
Однако мы их построим, так как легче оценить графики: в прогнозируемом графике отображается предсказанное октановое число с ограничениями неопределенности. Модель не работает при прогнозировании объектов номер 11-14. Программа снова обнаружила ошибочные образцы. (Это было также проверено человеком, который подготовил образцы. Они содержали алкоголь).
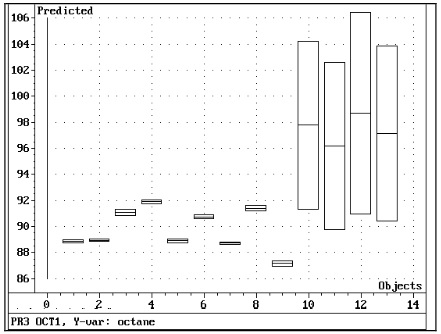
Рис. 7 Калибровочная модель OCT ver 1 была использована для прогнозирования октановых чисел в 14 новых образцах.
10. Модель регрессии PLS
Модель регрессии PLS связывает набор X-переменных (здесь спектров) с множеством Y-переменных (здесь октановые числа). Это достигается посредством набора абстрактных скрытых переменных, называемых ПК или основных компонентов. Каждый ПК представляет собой одно систематическое изменение данных.
Значение каждого ПК для каждого образца называется оценкой. Нагрузки представляют собой коэффициенты регрессии от каждой переменной до каждого ПК. Матричные уравнения, используемые для связи этих терминов:
Y = TP + E
X = TQ + F
где T = оценки ПК, P = X - переменные нагрузки, Q = Y - переменные нагрузки, E = X-остатки (ошибка) и F = Y - остатки.
Как только модель будет завершена, ее можно использовать для определения Y-переменных только на основе X-переменных. Модель регрессии лучше всего интерпретировать и анализировать, используя графическое представление терминов, как мы видели в этой заявке.
11. Традиционная модель регрессии
Однако программа Unscrambler также вычисляет B-коэффициенты, которые могут быть использованы для выражения отношений между X и Y как более общеизвестное уравнение регрессии;
Y = B0 + B1*X1 + B2*X2 + ... + BN*XN
Это уравнение часто реализуется, например, в моделях прогнозирования в режиме онлайн с помощью спектроскопических приборов или других измерительных приборов.
B-коэффициенты можно считывать из графика или таблицы:

Рис. 8. B-коэффициенты с использованием 3 ПК.
12. Выводы
Используя PLS с программным пакетом Unscrambler, мы смогли сделать калибровочную модель, которая давала очень точные прогнозы о нехимическом параметре октанового числа из спектроскопических данных. Программа автоматически обнаружила ошибочные образцы. Готовые графики позволили визуализировать калибровочную модель, упростив интерпретацию.
Источник: http://www.camo.com/downloads/resources/application_notes/Octane-number-prediction.pdf