Источник: Автоматизация технологических объектов и процессов. Поиск молодых
/ Cборник научных трудов ХVII научно-технической конференции аспирантов и студентов в г. Донецке 24-25 мая 2017 г. - Донецк : ДонНТУ, 2017. – 409 с.
УДК 62-551.452
Исследование робастности системы автоматического управления темпом загрузки шихты доменной печи
Быкова А. М., студ, Жукова Н. В., доц.,к.т.н
(ГОУ ВПО «Донецкий национальный технический университет», г. Донецк, ДНР)
Общая постановка проблемы. Исходной информацией для рассматриваемой системы служит величина заданного уровня засыпи и текущие показания зондовых и радиоактивных уровнемеров, на основе которых определяются скорость схода шихты в печь и величина рассогласования действительного и заданного уровней засыпи. Управляющим воздействием является порция шихтовых материалов на горизонтальный конвейер в соответствии с изменением скорости схода шихты в доменную печь. Поскольку объект управления имеет большое транспортное запаздывание τ и малую постоянную времени T такую, что τ/T >> 1, то авторами было предложено применить ПД – регулятор, а компенсацию времени запаздывания обеспечить за счет предиктора Смита [1]. Это позволило на основании прогнозируемой скорости схода шихты определить со значительным предварением требуемую производительность транспортера, и тем самым скомпенсировать большое запаздывание в системе загрузки [1].
При исследовании и моделировании данной системы управления имеет смысл представить процесс изменения скорости схода шихты как полигармонический с наложением широкополосного случайного шума. Такой процесс может быть достаточно точно представлен рядом Фурье:
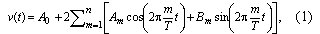
где  .
.
Если обозначить 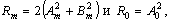 то дисперсия процесса скорости схода шихты v(t) , учитываемая одной гармоникой, равна
то дисперсия процесса скорости схода шихты v(t) , учитываемая одной гармоникой, равна  , а дисперсия, учитываемая различными гармониками, складываясь, дают общую дисперсию процесса σ2. Периодическая функция v(t) довольно точно аппроксимируется этими гармониками [2], так что (1) может быть использована для прогноза будущих значений скорости схода шихты.
, а дисперсия, учитываемая различными гармониками, складываясь, дают общую дисперсию процесса σ2. Периодическая функция v(t) довольно точно аппроксимируется этими гармониками [2], так что (1) может быть использована для прогноза будущих значений скорости схода шихты.
Таким образом, имеет смысл провести исследование динамики разработанной системы с учетом наложения случайных шумов на скорость схода шихты, а также с учет шумов, действующих в цепи измерения на величину уровня шихты на колошнике. Это позволит оценить робастность спроектированного ПД-регулятора, а также дать рекомендации по величине диапазонов изменения параметров объекта управления.
Методика решения. Информация, поступающая от уровнемеров, в реальных условиях зашумлена. Данный сигнал поступает на ошибку рассогласования с неопределённымипомехами, интенсивность зашумления в основном зависит от мощности помех – дисперсии. Скорость схода шихты, является производной по уровню, она также зашумлена. Мощность шума (дисперсию) в цепи измерения выбирается исходя из погрешности уровнемеров – 0,1, а мощность помех, влияющие на скорость схода шихты – 0,13[2]. Схема моделирования САУ темпа загрузки шихты с учетом шумов (рис.1).
Промоделируем систему при начальных коэффициентах ПД-регулятора (Kp=0.83, Kd=0.01 ) (рис.2).

Рисунок 1 – Схема моделирования САУ величиной уровня засыпи на колошнике с предиктором Смита
Из рис. 2 видно, что с учетом шумов при номинальных параметрах объекта a=1.25, b=0.7, c=1.6 имеет время переходного процесса 35 секунд, при худшем сочетании параметров a=1.75, b=0.735, c=1.68 - 25секунд. При сочетании параметров a=0.75, b=0.665, c=1.52 время регулирования составляет 45 сек. Во всех переходных процессах наблюдаются колебания на выходе системы, они превышают 2% критерий. Время регулирования во всех трех переходных процесса не удовлетворяет необходимому времени – желательно получить более затяжной процесс во всех случаях, несмотря на то, что процесс темпа загрузки должен происходить в пределах от 30 до 70 секунд, при разных уровнях засыпи шихты на колошнике. Как видно из рис. 2 при худшем сочетании параметров системы время регулирования выходит за установленные границы и не является робастной.
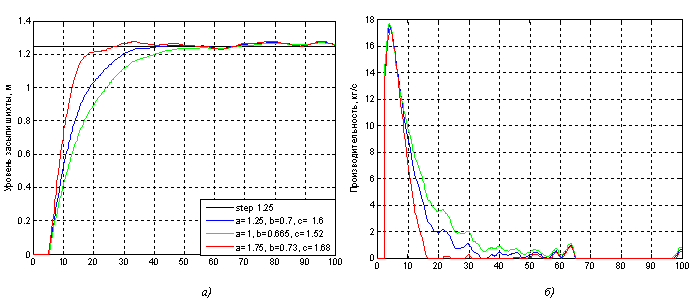
Рисунок 2 – а) переходные характеристики уровня засыпи на колошнике при изменении номинальных параметров объектас учетом шумов; б) производительность транспортера
Следовательно, для обеспечения робастности и желаемого качества переходных процессов при изменении параметров системы и при влияния на нее шумов используем инструментальный пакет CheckStepResponseCharacteristics (ранее называемый NCD). В качестве средства для достижения указанной цели принимается оптимизационный подход, обеспечивающий минимизацию функции штрафа за нарушение динамических ограничений. При помощи данного инструмента можно настраивать параметры нелинейной Simulink-модели, в качестве которых может быть заявлено любое количество переменных, включая скаляры, векторы и матрицы. Особую значимость имеет то обстоятельство, что в процессе настройки могут учитываться неопределенности параметрического типа математической модели, что позволяет синтезировать робастные законы управления [3]. Данный модуль оптимизирует линейные и нелинейные системыуправления автоматической подстройкой заданных параметров модели по ее реакции. Автоматическая оптимизация повышает точность и быстродействие систем, сокращает время проектирования систем управления [4].
Данный блок подключается на выход системы. Далее в настройках задаем время нарастания, в данном случае 45 сек., время установления – 70 сек, финальное значение – 1.25 и перерегулирование 1%. Все параметры выбираем исходя из переходного процесса при номинальных параметрах системы. Далее нажимаем ResponseOptimizationи задаем коэффициенты регулятора в DesignVars, предварительно заменив их буквенными значениями в PIDконтроллере и дав им начальные значения, и переменные варьирования UncVars, также предварительно заменив их буквенными значениями в модели и инициализировав их номинальными параметрами системы. В данном случае, коэффициент a будет варьироваться в пределах от 1 до 1,75, bот 0,63 до 0,77, с от 1,44 до 1,76 (рис.1). При задании таких параметров, к сожалению, NCDне справился с поставленной задачей, поэтому были выбраны параметры, предложенные самим эти блоком: варьирование параметров c и b остались неизменными; параметр aстал варьироваться в пределах от 1,1 до 1,3.
Получены следующие результаты (рис.3): во всех случаях наблюдается более затяжной процесс, время регулирования при номинальных параметрах составило 55 сек., при худших 35 сек., в последнем случае 68 секунд. Колебания наблюдаются при всех сочетаниях параметров, однако они не превышают 2% критерия. Уменьшилась производительность, если раньше она составляла 170 кг/с, то при использовании оптимизатора составляет 111 кг/с. Параметры ПД-регулятора подстроенные блоком CheckStepResponseCharacteristics: Kp=0.54, Kd=0.01.Из рис. 4 видно, при таких параметрах регулятора управляющее воздействие уменьшилось, если при начальных значениях максимальное управляющее воздействие достигало 1,1 В, то при Kp=0.54, Kd=0.01 не превышает 0,8 В. Ошибка рассогласования (рис.5) при Kp=0.54, Kd=0.01 стала больше.

Рисунок 3 – а) переходные характеристики уровня засыпи на колошнике при изменении номинальных параметров объекта с учетом шумов с блоком CheckStep; б) производительность транспортера с блоком CheckStep
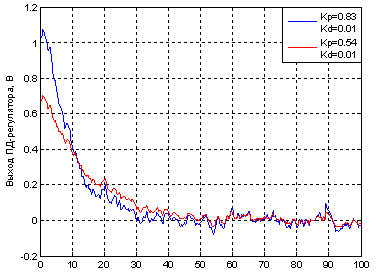
Рисунок 4 – Управляющее воздействие при разных коэффициентах регулятора
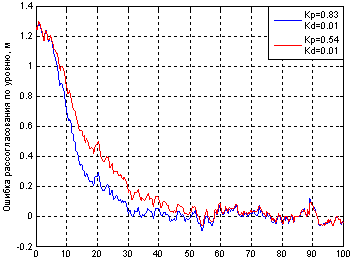
Рисунок 5 – Ошибка рассогласования при разных коэффициентах регулятора
Необходимо отметить, что выбранные коэффициенты ПД-регулятора, обеспечивающие робастность системы, Kp=0.54, Kd=0.01 были рассчитаны по критерию ИВМО. Эти коэффициенты минимизируют оценку ИВМО, при которых, система обладает удовлетворительной реакцией на единичное ступенчатое воздействие [5]. (рис.5).

Исходя из рис. 6 ошибка по критерию ИВМО при коэффициентах ПД-регулятора Kp=0.54, Kd=0.01 составляет 6,33×10-27.

Рисунок 6 – Оценка ИВМО при Kp=0.54, Kd=0.01
Выводы.
- Проведено моделирование системы автоматического прогнозного управления темпом загрузки доменной печи. Процесс изменения скорости схода шихты представлен как полигармонический с наложением широкополосного случайного шума с дисперсией равной 0,13. При моделировании также учтена погрешность в цепи измерения от датчиков уровня шихты на колошнике с дисперсией 0,1, а также возможные изменения параметром объекта управления в процессе загрузки. Это позволило эмитировать условия неопределенности для рассматриваемой системы с целью анализа робастности спроектированного регулятора и условий ограничений функционирования последнего.
- Результаты моделирования показали, что при изменении параметров объекта на 5%и 20% исходная система не обеспечивает требуемые показатели качества регулирования, в частности время регулирование при разных сочетания параметров объекта изменялось от 25 до 45 секунд, а также наблюдалась значительные колебания на выходе системы.
- Для обеспечения свойств робастности, исходные параметры ПД-регулятора (Kp=0.83 и Kd=0.01), рассчитанные по критерию минимума интеграла от взвешенного модуля ошибки, были оптимизированы с использованием пакета прикладных программ CheckStepResponseCharacteristics. При этом время переходного процесса не превысило допустимых границ от 35 до 70с, статическая ошибка на выходе системы при всех сочетаниях параметров не превышала 2 %. При коэффициентах ПД-регулятора Kp=0.54 и Kd=0.01 система является робастной, обеспечивает требуемые показатели качества регулирования.
Перечень ссылок
- Быкова А.М. Исследование динамики системы автоматического управления темпом загрузки шихты доменной печи. / А.М. Быкова, Н.В. Жукова. Завалишинские чтения: молодежная секция. Сб. докл. СПб.: ГУАП, 2016. – 210 c. С.21-23.
- Глинков Г.М. АСУ Технологическими процессами в агломерационных и сталеплавильных цехах: учебник для вузов / Глинков Г.М. , Маковский В.А. М.: Металлургия , 1981. – 360 с.
- Веремей Е.И. Пособие
NonlinearControlDesignBlockset
[Электронный ресурс]: Материалы по продуктам MATLAB & Toolboxes./ Веремей Е.И, Погожев С.В. – Режим доступа:http://matlab.http://matlab.exponenta.ru/nonlinecondes/book1/preface.php - Dr. BobDavidov. Автоматическая оптимизация Simulink моделей и регуляторов [Электронный ресурс] – Режим доступа: http://portalnp.ru/wpcontent/uploads/2013/10/05.01_MATLAB.-Simulink-Response-Optimization_Ed_2.pdf
- Дорф Р. Современные системы управления / Дорф Р., Бишоп Р. – М.: Лаборатория Базовых Знаний, 2002. – 832 с.: ил.