Автор:Gabriel Pérez
Источник: Электронная библиотека Arxiv.org [Электронный ресурс]. URL:https://arxiv.org/abs/0705.1744v1
Перевод с английского: Деговцов И.В.
Аннотация: В данной работе изучаются статистические данные о заклиниваниях и обвалах при моделировании процесса разгрузки двумерного силоса, заполненного полидисперсным материалом представленном в виде дисков. В соответствии с экспериментальными данными найдены экспоненциальные зависимости размеров обвалов для всех диаметров выходного отверстия. Средний размер обвала растет довольно быстро с диаметром выходного отверстия. Данные об этом росте лучше согласуются по критическому отклонению от большой критической экспоненты, как сообщалось для трехмерных экспериментов, чем при экспоненциальном росте для двухмерных экспериментов.
Высыпание гранулированного вещества из емкости является одним из наиболее распространенных явлений в повседневной жизни, но оно еще не до конца изучено. Будь то высыпание соли из солонки, кукурузы из бункера или гравия из грузовика, мы учитываем только несколько эмпирических правил, для объяснения данного процесса [1, 2]. В силу как своей интересности, так и очевидного практического применения, это явление привлекло внимание многих исследователей в последнее время.
Особенно простой и распространенный пример высыпания гранулированного вещества представляют бункеры и силосы [5]. В этих системах были определены три состояния течения: разбавленное (газообразное), густое (похожее на жидкость) и заклинившее (статическое, твердоподобное) [6, 7]. Переход от разбавленного к густому, как функция выходного отверстия, является прерывистым и имеет характер гистерезиса [7]. Известно, что в этих емкостях появляются заклинивания, как только размер выходного отверстия уменьшается до размеров нескольких средних диаметров частиц внутри. Экспериментальная работа как в 2-D, так и 3-D бункерах [8, 9] и силосах [4, 6, 7, 9, 10] показали, что заклинивание зависит только от соотношения размеров частиц и выходных отверстий, если диаметр и высота силоса достаточно велики, то есть силос находится в своем термодинамическом пределе
.
Среди многих вопросов, которые все еще остались в динамике силосов, одним из самых простых и фундаментальных является возможность существования критического размера отверстия, при котором поток не может замяться. Существование такого размера, а именно, критического значения для отношения R = размер-выходного-отверстия / размер-зерна, продемонстрировано в экспериментах для нескольких типов гранулированных сред, включая гладкие и шероховатые сферы, рисовые зерна и чечевицу [10]. Это несколько странный результат, поскольку та же работа показывает, что распределение величины обвала может быть очень хорошо подобрано экспоненциально, и это, в свою очередь, согласуется с простой моделью, где каждое зерно, либо кластер зерен, имеет заданную вероятность выхода из силоса, некоррелированного поведением других зерен (кластеров). Принимая эту модель, становится трудно понять, как полностью некоррелированный процесс может привести к корреляциям на большие расстояния, которые обычно связываются с критичностью. Следует также отметить, что эксперименты, проведенные в [8, 9], также подтверждают гипотезу о фиксированной вероятности выхода из силоса для каждого зерна, но указывают на вероятность заклинивания, которая экспоненциально убывает с ростом R; однако, в [9] также утверждают, что эти экспериментальные данные вполне могут соответствовать любому из двух вариантов поведения.
В этой работе мы провели симуляцию двумерного силоса с переменным размером отверстия, с целью получения статистических данных, связанных с процессом его разгрузки и о возможном наличии критичности в этом процессе. Хоть имитационные подходы и не могут полностью воспроизвести динамику реальных экспериментов, они действительно дают хорошие приближения к реальным потокам и должны иметь возможность находить признаки критического поведения, если они есть. Они имеют дополнительное преимущество, обеспечивающее непрерывную и неограниченную регулировку основных параметров потока. Но у такого моделирования есть очевидное ограничение, которое ставит его в невыгодное положение в отношении натурных экспериментов. Главным образом это тот факт, что отслеживание очень больших обвалов, которые появляются при больших размерах выходных отверстий, занимают чрезмерно большое количество машинного времени. Тем не менее, систематическое исследование обвалов для разных размеров выходных отверстий позволяет определить конкретные тенденции.
Данное моделирование было выполнено над набором из N полидисперсных дисков с диаметром, заданным di = dcp + xΔd, где dcp – средний диаметр, Δd – его максимальное отклонение, а x случайным образом выбирается из [-1, 1] по закону равномерного распределения. Силос имеет диаметр основания D и неопределенную высоту. Центр дна представляет собой отверстие размером dH. Диски имеют 2-мерную плотность массы σ, а гравитационное ускорение g действует отрицательно по оси координат z. При контакте диски взаимодействуют с (абсолютно жесткими) стенками силоса и друг с другом посредством линейной упругости с постоянным коэффициентом, который при загрузке имеет значение k, а при разгрузке уменьшается на коэффициент рекомбинации ε. Это реализация линейной упруго-амортизаторной модели [11, 12] с использованием подхода с двумя муфтами, приведенного в [13]. Этот подход обычно используется из-за его надежности и простоты. Взаимодействие дополняется динамическим и статическим трением, при этом для обоих используется одинаковый коэффициент μ. Для статической части тангенциальная упругая модель приведенная в [11], следует за конкретной формулировкой [12] с поправками, приведенными в [14]. Уравнения движения были интегрированы с использованием скоростного алгоритма Верле [14].
Единственный фиксированный численный вход в задаче задается гравитационной постоянной; все величины можно масштабировать, скажем, к естественным единицам, где средний диаметр и масса дисков установлены равными единице. В этой работе мы предпочли реализовать численный эксперимент со стандартными единицами и использовать N = 2000 дисков с dcp = 0.5, Δd = 0.05, D = 15, σ = 0.8 и k = 4 × 106, причем все величины приведены в системе СГС. Такое значение для k не так велико, как можно ожидать для некоторых жестких реальных систем (например, стальных или стеклянных сфер), но это позволяет повысить эффективность использования машинного времени. Оно может быть достаточно реалистичным для более мягких зерен, таких как рис или чечевица, используемых в [10]. Также сообщается, что изменения на один или два порядка в жесткости зерен мало влияют на результаты этих типов моделирования [16]. Для безразмерных величин μ и ε мы установили соответственно 0.5 и 0.9. Гравитация фиксируется как g = 981. Соотношение диаметров дисков и силоса дает D / dcp = 30, и для числа используемых дисков, бункер заполняется до высоты примерно в 2,5 раза больше, чем D. Эти два значения достаточно велики для того, чтобы поместить силос в термодинамический предел [4, 10, 17], по крайней мере, для трехмерного случая. Временной шаг составляет 0.01 от времени столкновения диска с диском tстолкн, которое для используемого здесь линейного взаимодействия задается выражением.
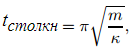
при этом, пренебрегая слабой зависимостью от ε. Для дальнейшего удобства мы также определяем шкалы времени и скорости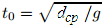 
и v0 = g t0.
Моделирование происходит следующим образом: сначала силос закрывается снизу, а диски помещаются в обычную сетку со случайными начальными скоростями. Затем позволяем системе перейти в состояние покоя только под действием силы тяжести вплоть до момента, когда обнаруженная максимальная скорость не будет составлять малую долю от v0. В этот момент, в дне силоса возникает отверствие даметром dh, и диски начинают высыпаться из него. Эти диски падают до тех пор, пока их центры не пройдут дистанцию ≈ 1.3 dcp ниже дна, и в этот момент они устраняются из выходящего потока и снова вводятся сверху системы на расстоянии 5.5 dcp от поверхности плотной совокупности дисков. При повторном введении, диски сохраняют их z-скорость, но их горизонтальная скорость равна нулю. Точка повторного введения выбрана так, чтобы удерживать верхнюю часть материала примерно плоский. При таких условиях наблюдаемый поток имеет смешанный тип, а не массовый либо воронкоподобный. Диски, расположенные ближе к центру силоса, падают быстрее, чем те, что близки к стенам, но разница в скорости не слишком велика.
Иногда над выпускным отверстием образуется свод, и поток останавливается. Учитывая то, что мы включаем в расчет статическое трение, эти своды не всегда выпуклые. Такое заблокированное состояние обнаруживается путем проверки того, что:
Было установлено, что для целей этого моделирования, значение c = 8 является адекватным. Как только эти два условия выполняются, силос получает толчок заданный вертикальным смещением zсмещ = A sin (2πνt), применяемым в течение половины периода. Для этого, мы использовали параметры A = 0.6 и ν = 8.0. В большинстве случаев этого толчка достаточно, чтобы сломать свод или своды, которые блокируют поток; однако, учитывая, что толчок перемещает весь материал параллельно, иногда случается так, что не хватает перестановки дисков чтобы разбить свод. Таким образом, возможно, что с этим методом разблокировки прохода можно получить нулевые обрушения. Это такие интервалы между двумя метками, когда из бункера не высыпается материал. Эти нулевые обрушения сильно коррелированы между собой, в том смысле, что для небольших отверстий они, как правило, появляются рядом друг с другом в записи времени. Этот тип событий также появился в экспериментах, опубликованных в [18]. Нулевые обрушения характерны для очень небольших размеров отверстий, и менее для больших.
Моделирование проводилось для размеров отверстий от 1.70 до 2.25 с шагом 0.05, соответствующего отношению R = отверстие / частица от 3.4 до 4.5 с шагом 0.1. Во всех случаях мы выполнили несколько прогонов, начиная с разных зерен 3 конфигураций. Для каждого размера мы получили не менее 1000 обрушений. Для всех соотношений дырок / частиц распределения лавин n (s) показывают в основном экспоненциальную форму, за исключением всплеска при s = 0 (нулевые обвалы) и слабого падения для малых s (см. рис.1). Эти две характеристики, вероятно, являются особенностью метода, используемого, чтобы разблокировать силос. Следует заметить, что уменьшение n (s), найденное для малых s, не столь ярко выражено, как указано в экспериментах [10]. Что же касается вероятности нахождения нулевых обвалов, то она идет от максимума 0.20 при R = 3.4 до минимума 0.019 при R = 4.4, но статистических данных недостаточно, чтобы предсказать их присутствие или отсутствие для больших значений R.
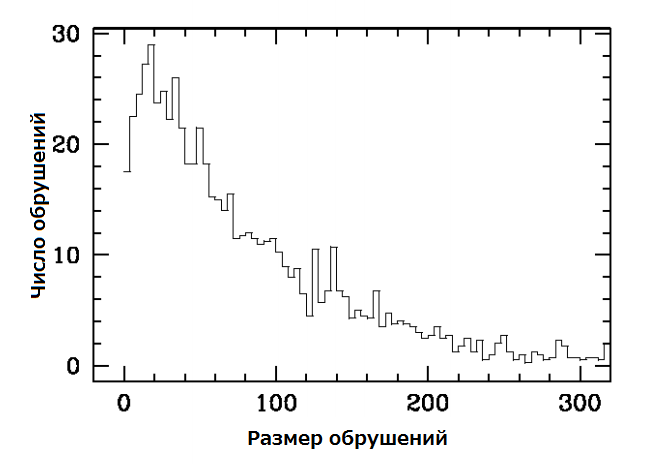
Рисунок 1 – Гистограмма обрушений
Чтобы избежать необходимости фиксировать размер бункера на гистограммах, мы использовали нормированное интегральное распределение
то есть мы подсчитываем количество обрушений с s или более дисками. Обратите внимание, что в таком измерении мы не учитываем нулевые обвалы. Для нормально нормированного экспоненциального распределения нормированное интегральное значение оказывается идентичным самому распределению. На рис. (2) показано интегральное распределение обвалов при R = 3.6.
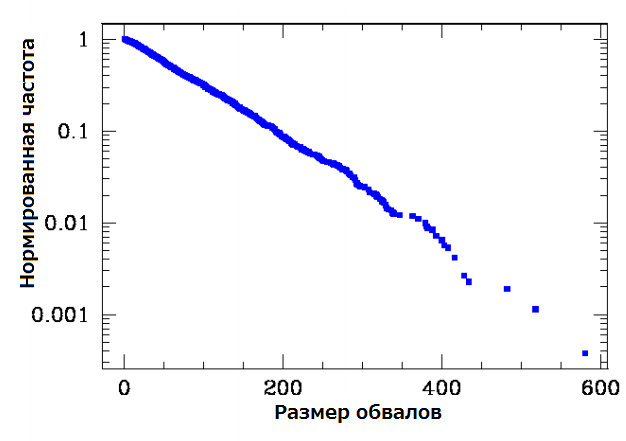
Рисунок 2 – Интегральное распределение обрушений
Учитывая требование, что распределение экспоненциально для всех случаев, должно быть возможно масштабировать s так, чтобы получить обвал всей совокупности. Это показано на рис. (3). Тем не менее, следует помнить, что распределение не является идеальной экспонентой из-за малой вероятности найденной для очень малых обвалов. Но вцелом этот эффект практически не ощутим.
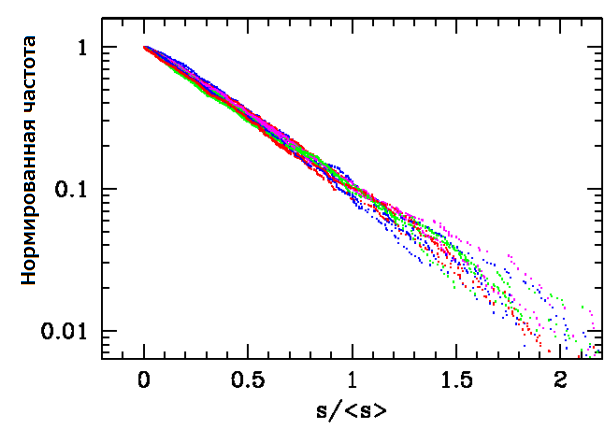
Рисунок 3 – Обрушение всей совокупности для всех значений R
Основной вопрос, который остается выяснить – это поведение обвала среднего размера ‹s› в зависимости от соотношения дыра / частица. Как и ожидалось, можно найти быстро растущую кривую. Этот рост можно интерпретировать как доказательство экспоненциальной расходимости формы ‹s(R)› ≈ s0 exp (R / R0), что означает, что существует ненулевая вероятность заклинивания для любого размера выходного отверстия, даже если для больших отверстий обычно они становятся невероятно большими. Однако, как указано в [9], также можно получить хорошее соответствие степенному закону формы ‹s(R)› ≈ s0 / (Rc-R)γ.
При попытке приспособить оба вида к результатам этого моделирования, мы обнаруживаем, что средние обвалы более соответствуют степенному выражению с Rc = 6.7 ± 0.4 и γ = 8.16 ± 1.10. Для этого соответствия, χ2 / dof составляет 0.41. Для экспоненциального получаем R0 = 0.768 и χ2 / dof 1.61. Два разных случая показаны на фиг.4 (4).
Рисунок 4 – Масштабирование ‹s› относительно R
Тогда ясно, что степенная расходимость благоприятствует экспоненциальному поведению; также ясно, однако, что с доступными данными разница между двумя вариантами на самом деле не достаточно велика, чтобы позволить сделать конкретный вывод. Более того, намекает на некоторые другие типы расхождений, такие как как существенно особая точка, ‹s› ≈ s0 exp [1 / (Rc - R)]. Тем не менее, результаты согласуются с наиболее обширными экспериментами, выполненными в это время, и поэтому добавляет поддержку существования критичности при заклинивании силосов. Это оставляет открытым более фундаментальный вопрос о происхождении корреляций, которые могут привести к критическому поведению в этом типе явлений.
* Electronic address: gperez@mda.cinvestav.mx