Автор: Н.П. Песков
Источник: Современные проблемы науки и образования. – 2011. – № 6.
Система оптимального управления ректификацией этаноламинов с использованием математической модели процесса
Этаноламины получаются путем насыщения концентрированного раствора аммиака окисью этилена и последующим фракционированием полученной смеси методом непрерывной ректификации.
Автоматизация процесса ректификации представляет собой сложную инженерную задачу вследствие большого числа регулируемых параметров, их взаимной связи, сложной и недостаточно изученной динамики процесса. К тому же ректификационная колонна – объект управления со значительной инерционностью и временем запаздывания по каналам управления [1].
Сегодня значительно расширились возможности автоматизации, контроля и регулирования процесса ректификации. Использование микропроцессорных контроллеров как центральных управляющих органов позволяет учесть более широкий спектр технологических требований и повысить надежность поддержания оптимального технологического режима.
Цель исследования состоит в создании системы оптимального управления ректификацией этаноламинов с использованием математической модели процесса непрерывной ректификации в колонне насадочного типа для предвидения величины управляющего воздействия, полностью компенсирующей возмущающие воздействия. Целью управления является поддержание заданного состава целевого продукта.
Первым этапом исследования стал анализ технологического процесса как объекта управления.
На исследуемой стадии производства получают товарные диэтаноламины (дистиллят) и триэтаноламины (кубовая жидкость) методом непрерывной ректификации в насадочной колонне.
Основными регулируемыми технологическими величинами являются составы дистиллята, кубового остатка. На чистоту этих целевых продуктов оказывает влияние ряд возмущающих воздействий процесса – состав сырья, параметры тепло– и хладагентов, давление в колонне и другие величины [2].
Основные управляющие воздействия – расходы флегмы в колонну и теплоносителя в кипятильник. Причем изменение расхода флегмы относительно быстро приводит к изменению состава дистиллята и одновременно с большим запаздыванием и в значительно меньшей степени – к изменению состава кубового остатка. Изменение же расхода греющего пара приводит в основном к изменению состава кубового остатка; состав флегмы при этом изменяется намного слабее.
Применительно к непрерывному процессу ректификации поддержание заданного по технологическому регламенту состава целевого потока является целью управления процессом. Состав потока, не содержащего целевого продукта, может меняться в определенных пределах вследствие изменения состава и скорости подачи исходного питающего потока. Возмущения по составу и расходу питающей смеси приводят к изменению давления, температуры, состава жидкости и паров в колонне. Но эти возмущения являются контролируемыми и могут быть учтены при реализации задач оптимального управления.
Наиболее сложным случаем управления ректификационной установкой является случай, когда целевыми потоками являются как поток дистиллята, так и поток кубовой жидкости. В таком случае требуется поддерживать заданный состав обоих потоков, а воздействие на состав кубовой жидкости или косвенно на ее температуру приводит к возмущению состава дистиллята через изменение расхода пара из кипятильника и, наоборот, воздействие на расход флегмы с целью стабилизации состава дистиллята влияет на состав кубовой жидкости. Взаимное влияние управляющих воздействий по обоим каналам на управляемые параметры вызывает дестабилизацию режима работы ректификационной колонны [5].
Трудности в одновременной стабилизации состава кубовой жидкости и дистиллята могут быть преодолены двумя способами. Первый способ состоит в автономном регулировании обоих параметров путем воздействия не только по основному каналу регулирования, например изменением расхода греющего пара в кипятильник, но и компенсируя возмущение по перекрестному каналу, например изменением расхода флегмы. Настроить такие контуры регулирования при соблюдении полной автономности довольно трудно. Второй способ состоит в управлении по возмущению с использованием математической модели насадочной ректификационной колонны. Функциональная структура подобной системы управления представлена на рис. 1.
Управление предполагается вести следующим образом. Датчики расхода FT и состава QT питающего потока (эти величины являются основными возмущающими воздействиями) измеряют текущие значения технологических параметров. Унифицированный выходной сигнал с датчика поступает на аналоговый вход (AI) микропроцессорного контроллера. Значение аналогового сигнала преобразуется в цифровой код, а затем в значение технологического параметра. Для измеренных текущих значений расхода и состава питающего потока с помощью математической модели находятся производительность кипятильника и расход флегмы (управляющие воздействия), при которых обеспечиваются требуемые составы кубовой жидкости и дистиллята. Требуемый расход флегмы (Lопт) выдается в качестве задания регулятору (FIC) расхода флегмы, а требуемая производительность кипятильника обеспечивается заданием (Pопт) по давлению греющего пара в рубашке кипятильника (регулятор PIC).
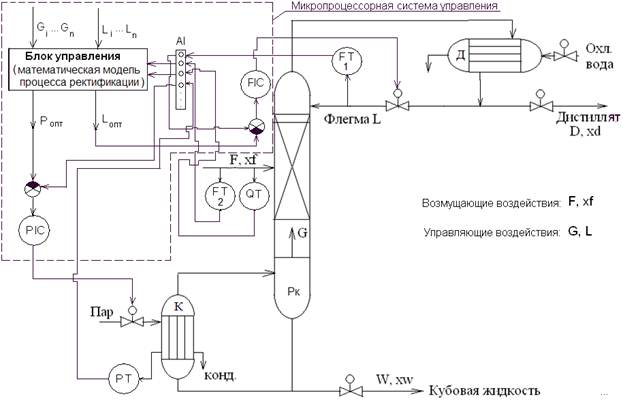Рис. 1. Функциональная структура системы управления процессом ректификации.
Основные обозначения (рис. 1): Рк – ректификационная колонна, К – кипятильник, Д – дефлегматор; FT1, FT2, PT, QT – датчики расхода флегмы, расхода исходной смеси, давления в рубашке кипятильника, состава исходной смеси соответственно; FIC, PIC – регуляторы расхода флегмы, давления пара в рубашке кипятильника; G – расход пара, L – расход флегмы, F – расход исходной смеси, xf – состав питающего потока, D – расход дистиллята, xd – состав дистиллята, W – расход кубовой жидкости, xw – состав кубовой жидкости, Pопт – оптимальное давление в рубашке кипятильника, Lопт – оптимальный расход флегмы.
Для осуществления поставленной цели необходимо решить следующие задачи:
Показателями качества управления могут быть такие свойства системы управления, как, например, энергетические затраты на управление, точность поддержания заданного режима работы объекта управления, время достижения цели управления, значение максимальной ошибки в определенном режиме функционирования, надежность безотказной работы, производительность и качество выпускаемой продукции, затраты сырья или электроэнергии, себестоимость продукции, мощность используемого оборудования и т.д. Конкретизация обобщенного показателя качества в общей теории оптимальных систем не осуществляется и проводится в каждой частной задаче индивидуально. Наиболее часто обобщенный показатель качества представляет функционал, и его можно описать в форме интегрального соотношения [7]:
J=
G (U (t), У (t), F (t), Х (t), t) dt, (1)
где U(t) – управление, Y(t) – управляемый процесс, F(t) – возмущения, X(t) – задающее воздействие, t – время.
Функция G определяет конкретный физический смысл показателя качества. Введение показателя (1) позволяет сформулировать задачу оптимального управления.
Задача оптимального управления заключается в следующем: в области допустимых управлений ? (U) следует найти такое допустимое управление U(t), при котором показатель качества (1) при заданных F(t), X(t) достигает экстремального значения:
J=extremum, U(t) є ? (U), (2)
а объект управления переводится из начального состояния Y(t0) в конечное Y(Т) є Q1, оставаясь в области допустимых состояний Y(t) є Q(Y) при всех t є [to, Т]. Условие (2) называют критерием оптимальности.
Критерий оптимальности в нашем случае – состав выходных целевых потоков (кубовой жидкости (xw) и дистиллята (xd)), заданный технологическим регламентом. Важно получить наилучший состав: xd>=xd,регл; xw<=xw,регл, где xd,регл, xw,регл – регламентные ограничения на состав дистиллята и кубовой жидкости соответственно, кмоль/кмоль.
Для контроля двух составов необходимо использовать комплексный показатель. Его определяют обычно с помощью функции желательности [6].
Рассмотрим построение функций желательности для ограничений:
Xd>=0.96 (3)
Xw<=0.04 (4)
Функция желательности d1 относится к ограничению (3), d1=1 (желательная функция), если ограничение (3) выполняется, и d1=0, если ограничение (3) не выполняется. С точностью до 0.01 функция желательности d1 определяется по следующей логической схеме:
Если xd<0.94, то d1=0;
если xd>0.96, то d1=1;
если xd>0.94 и xd<0.96, то d1=(xd–0.94)/0.02.
Аналогично d1 вводим функцию желательности d2, контролирующую выполнение ограничения (4). Величина d2 определяется по следующей логической схеме:
Если xw<0.04, то d2=1;
если xw>0.06, то d2=0;
если xw>0.04 и xw<0.06, то d2=(0.06–xw)/0.02.
Графически функции желательности d1 и d2 представлены на рис. 2.
Рис. 2. Функции желательности, контролирующие выполнение ограничений.
Комплексный показатель, контролирующий выполнение обоих ограничений (3) и (4), может быть представлен как геометрическое среднее частных функций желательности:
Если удается добиться того, чтобы D=1, то выполняются оба ограничения по составу выходных потоков процесса ректификации. Оптимизационная задача управления процессом состоит в определении значений расхода флегмы и производительности кипятильника, при которых D=Dmax.
Для решения поставленной задачи используется математическая модель процесса ректификации в колонне насадочного типа, которая состоит из системы уравнений, определяющей распределение концентрации в потоках пара и жидкости по высоте колонны [4]. Для построения модели вся насадочная часть колонны высотой H разбивается на бесконечно малые элементы величиной dh, и для каждого такого элемента записываются: основное уравнение массопередачи [3] (для жидкой и паровой фаз, для укрепляющей и исчерпывающей частей колонны), рассчитываются мольные доли легколетучего компонента в жидкой и паровой фазах на каждом элементарно малом участке насадки (рис. 3). В результате итерационного метода решения данной системы уравнений находим реальные значения концентраций кубовой жидкости и дистиллята при определенных условиях работы колонны. И в математическом обеспечении системы управления закладывается эта модель с применением метода сканирования к определению оптимального режима работы колонны.
Рис. 3. Математическое моделирование объекта управления.
Основные обозначения (рис. 3): x, y – концентрация легколетучего компонента соответственно в жидкой и паровой фазах элементарного объема насадки; x1, y1 – концентрация легколетучего компонента соответственно в жидкой и паровой фазах в начале элементарного объема насадки; x2, y2 – концентрация легколетучего компонента соответственно в жидкой и паровой фазах в конце элементарного объема насадки; dy – приращение мольной доли легколетучего компонента в паровой фазе элементарного объема насадки; dx – приращение мольной доли легколетучего компонента в жидкой фазе элементарного объема насадки; y* – равновесная мольная доля легколетучего компонента; Ky – коэффициент массопередачи; S – поверхность контакта фаз; H – высота слоя насадки; dh –высота элементарного объема рассматриваемой насадки; G – расход паровой фазы на выходе из колонны; L – расход флегмы в насадочную колонну. F – расход питающего потока.
Математическая модель, представленная системой уравнений на рис. 3, может быть использована для управления процессом ректификации по возмущению. Для измеренных значений расхода F питающего потока и его состава xf (возмущающие воздействия) с использованием математической модели рассчитываются оптимальные значения расхода флегмы (Lопт) и производительности (Gопт) кипятильника (управляющие воздействия), при которых обеспечиваются заданные составы кубовой жидкости и дистиллята. Найденное значение расхода флегмы выдается в качестве задания регулятору расхода флегмы, а найденная производительность кипятильника обеспечивается заданием по давлению пара в рубашке кипятильника.
Таким образом, предложенный алгоритм оптимального управления процессом непрерывной ректификации этаноламинов в колонне насадочного типа позволит своевременно обнаруживать нестандартные ситуации при работе системы и принимать необходимые меры по их нейтрализации, что в конечном итоге позволит улучшить качество продукта, увеличить производительность установки, сэкономить энергоресурсы. Имитационное моделирование процесса ректификации проводилось в пакете MATLAB. Планируется внедрение системы управления на реально действующей установке.
Рецензенты:
Автоматизация и информационные системы;, Дзержинский политехнический институт (филиал) Нижегородского государственного технического университета им. Р.Е. Алексеева, г. Дзержинск.
НИИ полимеров;, г. Дзержинск.