Преобразование детерминированных конечных автоматов в регулярные выражения

1 Предпосылки

Основная статья Клини определяет регулярные выражения и их связь с конечными автоматами [7]. Клини доказывает эквивалентность конечных автоматов и регулярных выражений, тем самым предоставляя нам первый метод – транзитивный метод замыкания для преобразования детерминированных конечных автоматов (ДКА) в регулярные выражения. Позже Бжозовский расширил метод Клини, введя понятие производных регулярных выражений [3], но его статья не была оцененан должным образом, пока Г. Берри и Р. Сетхи не вывели на передний план статью Бжозовского в [2]. Метод удаления состояний представлен в [4], но Линц представляет более простой метод в [8].

2 Определения

Мы будем использовать модель Мура [9] для конечных автоматов. Для автомата M с входным алфавитом A_k = {0, 1, ···, k - 1} M имеет m состояний M_s = {q1, q2, ···, qm}, где qλ – начальное состояние M и M_f = {qf1, qf2, ···, qfn} – n конечных состояний M, где n ? m. Для ясности мы будем использовать буквы для представления каждого значения в алфавите А вместо использования числового представления (a = 0, b = 1, и т.д.), а для удобства предположим, что q1 является исходным состоянием, если не указано иное.

Мы будем использовать определение Клини [7] регулярных выражений. Регулярные выражения определяются рекурсивно как:

1. Символы 0, 1, ..., k – 1, λ и φ являются регулярными выражениями, где λ – пустая строка, а φ – пустое множество.
2. Установить соединение: если заданы регулярные выражения x и y, объединение x и y, выраженное как x + y, является регулярным выражением.
3. Конкатенация: учитывая регулярные выражения x и y, конкатенация (или произведение) x и y, выраженное как xy, является регулярным выражением.
4. Итерация: если задано регулярное выражение x, итерация (или звездочка) x, выраженная как x*, является регулярным выражением.
5. Для регулярного выражения x, (x) является регулярным выражением.
6. Все регулярные выражения могут быть построены путем конечного применения правил 1-5.

Регулярные выражения в правиле 1 – терминалы. Конкатенация терминалов – это строка. Для данного регулярного выражения x существует множество X, которое содержит все строки, представленные x. Мы будем использовать x и X взаимозаменяемо. Одна строка просто представлена набором, содержащим эту единственную строку.

Мы также будем ссылаться и использовать следующие тождества:

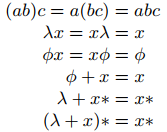
Так как + коммутативна, применяются все коммутативные версии.

3 Метод транзитивного закрытия

Предположим, что данный ДКA M должен быть представлен как регулярное выражение

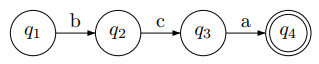
Рисунок 1 – Пример простого автомата

Рассмотрим автомат на рисунке 1. Вход для ребра в автомат является регулярным выражением. Достаточно просто, что регулярное выражение для перехода от q1 к q2 равно b, переход от q2 к q3 равен c и т.д. Более того, регулярное выражение, представляющее переход от q1 к q3, является конкатенацией регулярных выражений, образующих bc. Таким образом, мы можем найти регулярное выражение для автомата bca, так как это выражение является конкатенацией всех переходов из начального состояния q1 в конечное состояние q4

В более общем плане, для пути от q_λ до q_f, конкатенация регулярного выражения для каждого перехода в пути образует регулярное выражение, которое представляет ту же строку, что и путь от q_λ до q_f в автомате. Предположим, что существует единственный единственный путь в автомате M из q_λ до q_f, существует только одно регулярное выражение R такое, что R представляет ту же строку, что и ДКA M. Однако это тривиальный автомат, рассмотрим, как развернуть его в более общий случай.

Рисунок 2 – Пример более сложного автомата

Теперь рассмотрим ДКА на рисунке 2. Ясно, что между q1 и q2 существует несколько путей. Мы не можем получить простое регулярное выражение для представления ДКА, однако, используя другие операторы (объединение и итерация), мы можем опираться на наш предыдущий подход для создания конструкции, которая работает для всех типов ДКА. Мы откажемся от доказательства и оставим его Клини [7]. Доказательство также продемонстрировано Хопкрофтом и Ульманом [5] и достаточно ясно объяснено Саломаа [10].

Предположим, что регулярное выражение R_ij представляет собой совокупность всех строк, которые переводят автомат M из q_i в q_j. Кроме того, предположим, что представляет множество всех строк, которые переводят автомат M из q_i в q_j, не проходя через любое состояние выше q_k. Мы можем построить R_ij путем последовательного построения 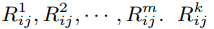, рекурсивно определяемого как

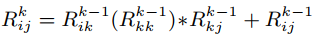
предполагая, что мы инициализировали :

Как мы видим, эта последовательная конструкция создает регулярные выражения, пока мы не получим R_ij. Затем мы можем построить регулярное выражение, представляющее M как объединение всех R_λf, где q_λ – начальное состояние и f ∈ M_f (конечные состояния для M).

Этот метод похож по характеру на проблему с парными краткими путями. Единственное отличие состоит в том, что мы принимаем объединение и конкатенацию регулярных выражений вместо суммирования расстояний. Это решение имеет ту же форму, что и транзитивное замыкание, и относится к совокупности задач, связанных с замкнутыми полукольцами.

Основная проблема подхода транзитивного замыкания состоит в том, что он создает очень большие регулярные выражения. Изучая формулу для , ясно, что значительная длина обусловлена повторным объединением конкатенированных терминов. Даже используя предыдущие идентификаторы, мы все еще имеем длинные выражения.

4 Метод удаления

Подход удаления состояния определяет шаблоны внутри графика и удаляет состояния, создавая регулярные выражения вдоль каждого перехода. Преимущество этого метода в отношении метода транзитивного закрытия заключается в том, что его легче визуализировать. Этот метод описан Ду и Ko [4], но мы рассмотрим гораздо более простой подход, который дает Линц [8].

Во-первых, любые мульти-ребра объединены в одно ребро, которое содержит объединение входов. Предположим, что от q2 до q5 существует ребро a и ребро b, которые будут объединены в одно ребро q2 до q5, которое имеет значение a + b.

Теперь рассмотрим подграф автомата M, который имеет вид, приведенный на рисунке 3. Состояние q может быть удалено, и автомат может быть приведен к форме на рисунке 4. Шаблон может по-прежнему применяться, если края отсутствуют. Для края, который отсутствует, опустить соответствующий край на рисунке 4.

Этот процесс повторяется до тех пор, пока автомат имеет вид, как на рисунке 5. Затем путем непосредственного расчета, регулярное выражение становится равно:

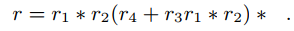
Рисунок 3 – Желаемый шаблон для удаления состояния

Рисунок 4 – Результаты после удаления состояния

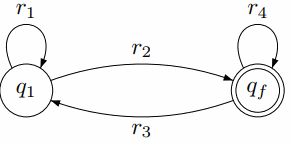
Рисунок 5 – Финальная форма

5 Алгебраический метод Бжозовского

Метод Бжозовского [3] использует уникальный подход к генерации регулярных выражений. Мы создаем систему регулярных выражений с одним регулярным выражением, неизвестным для каждого состояния в M, а затем мы решаем систему для R_λ, где R_λ – регулярное выражение, связанное с начальным состоянием q_λ. Эти уравнения являются характеристическими уравнениями М.

Построение характеристических уравнений является простым. Для каждого состояния q_i в M уравнение для R_i является объединением термов. Каждый член может быть построен так: для перехода a из q_i в q_j этот член является aR_i. Если R_i – конечное состояние, λ также является одним из термов. Это приводит к системе уравнений вида:

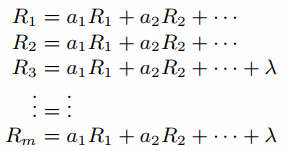
где 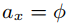если нет перехода от R_i к R_j.

Система может быть решена с помощью простой подстановки, за исключением случаев, когда неизвестное появляется как в правой, так и в левой части уравнения. Такая ситуация возникает, когда для состояния qi существует петля. Теорема Ардена [1] является ключом к решению этих ситуаций. Теорема такова:

Мы используем это уравнение для выделения R_i по левому размеру и последовательно подставляем R_i в другое уравнение. Мы повторяем этот процесс, пока не найдем R_λ без каких-либо неизвестных с правой стороны.

Например, снова рассмотрим автомат на [рисунке 2]. Характеристические уравнения следующие (где Rλ = R1):

Мы решаем для R2, используя теорему Ардена и ранее упомянутые тождества:

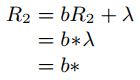
Подставим в R1 и разрешим:

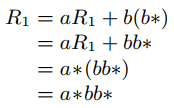
Таким образом, регулярное выражение для автомата на рисунке 2 равно a*bb*.

Выводы

Метод удаления состояний представляется полезным для определения регулярных выражений посредством ручного контроля, но не так просто реализeем в качестве транзитивного подхода закрытия и алгебраического подхода. Переходный подход закрытия дает ясную и простую реализацию, но имеет тенденцию создавать очень длинные регулярные выражения. Алгебраический подход является элегантным, опирается на рекурсивный подход и генерирует достаточно компактные регулярные выражения. Метод Бжозовского особенно подходит для рекурсивно ориентированных языков, таких как функциональные языки, где переходный подход закрытия будет громоздким для реализации.

Литература

1. Dean N. Arden. Delayed-logic and finite-state machines. In Theory of Computing Machine Design, pages 1–35. U. of Michigan Press, Ann Arbor, MI, 1960.
2. G. Berry and R. Sethi. From regular expressions to deterministic automata. TCS: Theoretical Computer Science, 48:117–126, 1987.
3. Janusz A. Brzozowski. Derivatives of regular expressions. J. ACM, 11(4):481–494, 1964.
4. Ding-Shu Du and Ker-I Ko. Problem Solving in Automata, Languages, and Complexity. John Wiley & Sons, New York, NY, 2001.
5. John E. Hopcroft and Jeffery D. Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, Reading, MA, 1979.
6. Richard Y. Kain. Automata Theory: Machines and Languages. Robert E. Krieger Publishing Company, Malabar, FL, 1981.
7. S. C. Kleene. Representation of events in nerve nets and finite automata. In Automata studies, pages 3–40. Ann. of Math. Studies No. 34, Princeton University Press, Princeton, NJ, 1956.
8. Peter Linz. An introduction to Formal Languages and Automata. Jones and Bartlett Publishers, Sudbury, MA, third edition, 2001.
9. E. F. Moore. Gedanken experiments on sequential machines. In Automata Studies, pages 129–153. Ann. of Math. Studies No. 34, Princeton University Press, Princeton, NJ, 1956.
10. Arto Salomaa. Jewels of Formal Language Theory. Computer Science Press, Rockville, MD, 1984.