Горяйнова Анастасия Вячеславовна
Системы искусственного интеллекта
Реферат по теме выпускной работы
Содержание
- Введение
- 1. Цели, задачи и планируемые результаты
- 2. Актуальность темы
- 3. Обзор исследований и разработок
- 3.1 Обзор международных источников
- 3.2 Обзор национальных источников
- 3.3 Обзор локальных источников
- 4. Постановка задачи и полученные результаты
- Выводы
- Список источников
Введение
Конечный автомат (state machine) – модель, которую удобно использовать в самых различных областях, начиная от моделирования логических устройств в технической диагностике и заканчивая структурированием приложений. В частности, одним из приложений конечных автоматов является моделирование неисправностей дискретных устройств. Часто такие неисправности можно описать как переброску дуг в автомате при сохранении выходных реакций.
Представляют интерес такие переброски, которые не изменяют поведения автомата. Известен ряд работ, в которых исследуются свойства перебросок такого рода. В настоящей работе продолжается исследование свойств автоматов, подверженных переброске дуг при условии, что автомат групповой и не изменяет своего поведения под действием переброски.
Будем говорить, что автомат допускает переброску, если в результате неё получается автомат, изоморфный исходному. Такую переброску будем называть допустимой, а допустимую переброску k-дуг, будем называть k-переброской.
Цели, задачи и планируемые результаты
Объектом исследования является поведение конечного приведенного группового автомата при переброске дуг.
Предметом исследования является выявление условий, при которых, автомат допускает переброску k-дуг, сохраняя при этом изоморфизм и свойство быть групповым.
Целью магистерской диссертации является разработка и исследование метода анализа групповых автоматов и допустимых ими перебросок дуг.
Основные задачи работы:
- провести анализ поведения группового автомата в результате переброски k-дуг, где k ≥ 1;
- выяснить существование допустимых k-перебросок и описать структуру автоматов, допускающих их;
- разработать алгоритм построения допустимых k-перебросок;
2. Актуальность темы
Модель конечного автомата прошла хорошую проверку временем. Использование конечных автоматов позволяет разработчикам создавать хорошо организованные логические системы с гибкими возможностями, а также анализировать их поведение в различных условиях.
Например, в играх часто используют различные персонажи, которые перемещаются в области игры и могут действовать в различных режимах. Использование конечных автоматов с четко определенными правилами для каждого персонажа, определяющими возможные варианты его поведения в различных состояниях и допустимые переходы из одного состояния в другое, позволяет создавать сложные варианты поведения как персонажей, управляемых компьютером, так и персонажей, управляемых пользователем [1].
Настоящая работа относится к теории экспериментов с автоматами. Экспериментом называют процесс подачи на автомат последовательности входных сигналов, наблюдение соответствующей реакции автомата и вывод заключения о функционировании и свойствах автомата, основанных на этих наблюдениях и априорной информации об автомате. Основная задача теории экспериментов состоит в разработке эффективных экспериментов, позволяющих получить определенные сведения о строении автомата, его функциях, о характеристиках процесса преобразования информации, осуществляемого этим автоматом.
Таким образом, исследование модели конечного автомата и изучение его поведения является актуальной задачей.
3. Обзор исследований и разработок
3.1 Обзор международных источников
Автоматы, близкие по поведению в том или ином смысле, исследуются достаточно давно, равно, как и структура классов таких автоматов. В основном, эта задача рассматривается в рамках теории экспериментов с автоматами.
Основание теории экспериментов с автоматами было положено Муром [2]. В его работах исследование проводилось в двух направлениях: неотличимость автоматов никаким кратным и никаким простым экспериментом, а также распознавание автомата и его состояний с помощью таких экспериментов. В дальнейшем теория экспериментов получила развитие в работах Ф. Хенни, Мили, Брауэра и других [3-6]. Методы и результаты анализа автоматов и алгоритмов проведения экспериментов с ними достаточно полно представлены в известной книге А. Гилла [7].
3.2 Обзор национальных источников
Отечественные работы в области экспериментов с автоматами связаны с именами A.M. Богомолова и его учеников, М.П. Василевского, В.Н. Носкова, Н.В. Евтушенко, А.Ф. Петренко, И.К. Рысцова, В. А. Твердохлебова, С.В. Яблонского, В.Б.Кудрявцева и др. [8-16].
Теория экспериментов интенсивно развивается и в настоящее время. В [17-18] получен ряд результатов, связанных с анализом поведения автоматов в условиях воздействия на них факторов внешней среды. В ряде работ изучалось влияние перебросок дуг на поведение автомата. В теории графов также рассматривались родственные задачи, где изучалась задача определения, когда один из графов (автомат) может быть получен из другого в результате некоторой последовательности перебросок дуг [19].
3.3 Обзор локальных источников
В донецком национальном техническом университете (кафедра системного анализа и искусственного интеллекта) поведение автомата, подверженного переброскам дуг, исследовалось в работах Копытовой О. М, Бурлаевой Е. И., Швец О.А. и др. В [20-24] получены следующие основные результаты:
- переброска одной дуги в приведенном автомате Мили всегда приводит к неизоморфному автомату;
- переброска двух дуг может порождать автомат, эквивалентный исходному;
- для любого натурального k > 1 существует приведенный автомат, в котором найдется подмножество из k дуг, одновременная переброска которых приводит к изоморфному автомату;
- при переброске двух дуг вход-выходные отметки на перебрасываемых дугах должны совпадать;
- возможны переброски более двух дуг, при которых вход–выходные отметки на перебрасываемых дугах различны;
- получен ряд необходимых и достаточных условий, при которых переброска двух дуг сохраняет изоморфизм исходного и преобразованного автоматов;
- представлена структура автоматов, в которых возможна переброска любого числа дуг ≥ 2, причем эти автоматы не являются сильно связными;
- показано, что переброска дуг, сохраняющая изоморфизм, возможна в автоматах, обладающих определенной симметрией графа переходов, которая отражается и в циклической структуре графа;
- существуют примеры сильно связных автоматов, в которых существует ≥ 3–х перебросок, сохраняющих изоморфизм.
Как видим, для произвольного приведенного автомата пока не получен критерий сохранения изоморфизма при перебросках дуг. В настоящей работе исследуется частный случай перебросок, а именно, переброски в групповых автоматах.
4. Постановка задачи и полученные результаты
Автомат называется групповым, если в нем переход по каждому входному символу задает некоторую перестановку на множестве состояний. Как известно, множество перестановок n элементов с операцией композиции на нём является группой.
Под автоматом будем понимать приведенный автомат Мили А (S, Х, Y, δ, λ), где S, Х, Y – множества состояний, входных и выходных символов соответственно, а δ, λ – функции переходов и выходов, причем ∀ x: { δ(s, x) | s ∈ S} = S.
Напомним определение приведенного автомата. Два состояния s и t одного и того же автомата A или двух разных автоматов A и B соответственно, называются эквивалентными если для всякого входного слова р∈X* выполняется λ(a,p)=λ′(b,p), где λ ′ – функция выходов автомата A или B. Автомат называется приведенным, если все его состояния попарно неэквивалентны. Каждому состоянию s поставим в соответствие множество λs всех вход-выходных слов, порождаемых этим состоянием.
Автомат в нашем случае удобно задавать в виде графа переходов, вершины которого соответствуют состояниям из S, а дугами являются четверки (s,x,y,t), где t = δ (s,x), y = λ(s, x). Пара (x,y) называется отметкой дуги, s – ее началом, а t – концом. Если e=(t, x, y, u) – дуга в графе переходов автомата A, то переброской этой дуги из состояния u в состояние v, отличное от u, называем замену её дугой (t,x,y,v).
Влияние перебросок дуг на поведение автомата будем изучать следующим образом:
- cначала рассмотрим переброску ровно одной дуги;
- затем сформулируем результаты касающиеся переброски ровно 2-х дуг;
- после этого перейдем к изучению переброски k-дуг, где k > 2;
К настоящему времени получены следующие результаты:
Теорема 1. Переброска одной дуги в групповом автомате всегда приводит к неизоморфному автомату.
Действительно переброска дуги (sk, x, y, sk+1) в состояние sj ≠ sk+1 приводит к тому, что состояние sk+1 перестает быть преемником какого-либо состояния по входному символу x, т.е. автомат перестает быть групповым.
Теорема 2. Переброска двух дуг в групповом автомате всегда приводит к неизоморфному автомату.
Доказательство основано на том очевидном факте, что у изоморфных автоматов для любого входного символа существует одинаковое число циклов.
Покажем, что в результате переброски двух дуг это свойство нарушается.
Пусть дуга (sk, x, yk, sk+1) перебрасывается в состояние sj ≠ sk+1, т.е. заменяется дугой (sk, x, yk, sj). Возможны два случая: 1) sj принадлежит тому же циклу, что и sk+1 и 2) sj принадлежит другому циклу. Пусть до переброски состояние sk принадлежит некоторому циклу по x:
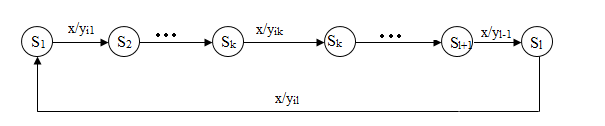
Рисунок 1 – Цикл по x длины 1 ≤ l
Рассмотрим первый случай, который наглядно показан на рисунке 2.
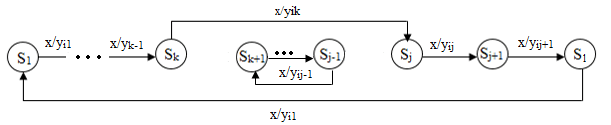
Рисунок 2 – Переброска двух дуг в цикле по xi длины n
Из рисунка видно, что для сохранения автоматом свойства быть групповым
в нём необходимо перебросить дугу (sj-1, x, yij-1, sj) в состояние sk+1, т.е.
заменить её дугой (sj-1, x, yij-1, sk+1). Нетрудно видеть, что в результате
таких двух перебросок один цикл по х (показанный на рисунке 1) заменяется
двумя циклами (показанными на рисунке 2), т.е. количество циклов по х увеличивается.
Рассмотрим второй случай, когда состояния sk+1 и sj принадлежат разным циклам – как показано на рисунке 3.
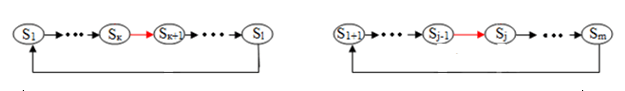
Рисунок 3 – Два цикла по x
После переброски дуги (sk, x, yk, sk+1) в состояние sjдля сохранения
автоматом свойства быть групповым
в нём необходимо перебросить дугу
(sj-1, x, yj-1, sj) в состояние sk+1, т.е. заменить её дугой
(sj-1, x, yj-1, sk+1).
Нетрудно видеть, что в результате переброски дуг вместо двух циклов
по x получаем один цикл (показанный на рисунке 4).
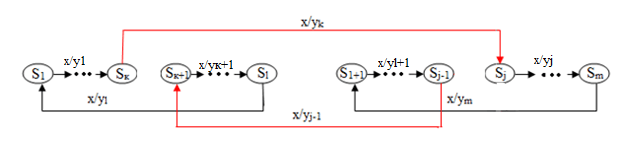
Рисунок 4 – Переброска двух дуг между циклами
Изменение числа циклов по х в обоих случаях доказывает теорему.
Теорема 3. Для любого к ≥ 3 существует групповой автомат, допускающий переброску k-дуг.
Доказательство.Построим групповой автомат с числом состояний k ≥ 3, двумя входными и двумя выходными символами {0,1}. По 0 автомат содержит один цикл, причем все состояния с первого по (k-1)-ое выдают реакцию 0, а k-ое состояние выдает реакцию 1. По 1 для всех состояний имеется петля с выходным символом 0 (показано на рисунке 5).
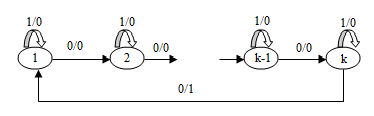
Рисунок 5 – Общий вид группового автомата
Легко видеть, что автомат приведенный и групповой. Выполним следующие переброски: изменим направление всех дуг по 0 на обратное (показано на рисунке 6).
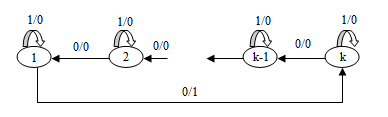
Рисунок 6 – Групповой автомат после переброски k-дуг
Ясно, что в результате переброски получаем автомат изоморфный исходному.
Приведём пример переброски четырех дуг.
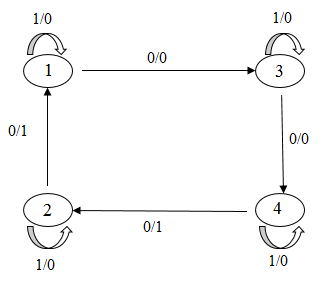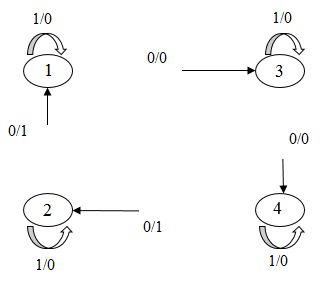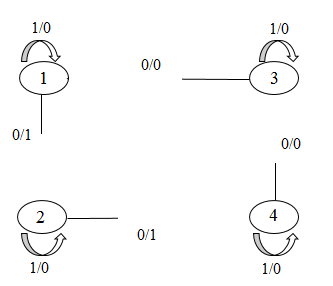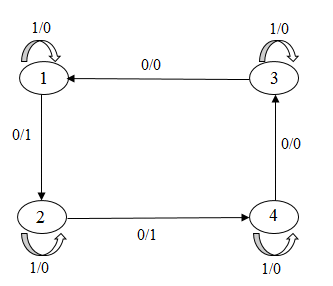
Рисунок 7 – Переброска 4-х дуг в групповом автомате
(анимация: 17 кадров, 3 цикла повторения, 82,1 килобайт)
Выводы
К настоящему времени получены следующие результаты:
- доказано, что переброска одной и двух дуг всегда приводит к неизоморфному автомату;
- доказано, что для любого к ≥ 3 существует групповой автомат, допускающий переброску k-дуг;
- приведен пример переброски четырех дуг с сохранением изоморфизма;
При написании данного реферата магистерская работа еще не завершена. Окончательное завершение: июнь 2017 года. Полный текст работы и материалы по теме могут быть получены у автора или его руководителя после указанной даты.
Список источников
- Салмре И. Программирование мобильных устройств на платформе .NET Compact Framework / И. Салмре. – М.: Вильямс, 2006. – 702 с.
- Мур Э.Ф. Умозрительные эксперименты с последовательностными машинами / Э.Ф. Мур // Автоматы. – М.: Иностранная литература, 1956. – С. 179-210.
- Hennie F. C. Fault detecting experiments for sequential circuits / F. C. Hennie // Proc. 5 Annual Symp. Switch. Circuits Th. and Logic. Design. – 1964. – P. 95-110.
- Bhattacharyya A. Checking experiments on sequential machines / A. Bhattacharyya. – New York: J. Wiley and Sons, 1989. – 155 p.
- Kohavi Z. Switching and finite automata theory / Z. Kohavi. – New York: Mc Graw Hill, 1970. – 522 p.
- Брауэр Р. Введение в теорию конечных автоматов / Р. Брауэр. – М.: Радио и связь, 1987. – 392 с.
- Гилл А. Введение в теорию конечных автоматов / А. Гилл. – М.: Наука, 1966. – 272 с.
- Богомолов А.М., Барашко А.С., Грунский И.С. Эксперименты с автоматами / А.М. Богомолов, А.С. Барашко, И.С. Грунский. – Киев: Наукова думка, 1973. – 144 с.
- Богомолов А.М., Грунский И.С., Сперанский Д.В. Контроль и преобразования дискретных автоматов / А.М. Богомолов, И.С. Грунский, Д.В. Сперанский. – Киев: Наукова думка, 1975. – 176 с.
- Богомолов А.М., Салий В.Н. Алгебраические основы теории дискретных систем / А.М. Богомолов, В.Н. Салий. – М.: Наука, 1997. – 386 с.
- Евтушенко Н.В., Матросова А.Ю. К синтезу контролепригодных автоматных сетей / Н.В. Евтушенко, А.Ю. Матросова // Техническая диагностика. – 1991. № 3. – С. 143-152.
- Евтушенко Н.В., Петренко А.Ф. Метод построения проверяющих экспериментов для произвольного недетерминированного автомата / Н.В. Евтушенко, А.Ф. Петренко // Автоматика и вычислительная техника. – 1990. № 5. – С. 73-76.
- Евтушенко Н.В., Петренко А.Ф. О проверяющих возможностях кратных экспериментов / Н.В. Евтушенко, А.Ф. Петренко // Автоматика и вычислительная техника. – 1989. № 3. – С. 9-14.
- Петренко А.Ф. Эксперименты над протокольными объектами / А.Ф. Петренко // Автоматика и вычислительная техника. – 1987. № 1. – С. 16-21.
- Petrenko A.F., Yevtushenko N., Dsouli R. Grey box finite state machine base testing strategies / A.F. Petrenko, N. Yevtushenko, R. Dsouli // Depart d’informatique et recherch. operat. Univ de Moutreal, 1994. Publ 991. – 22 p.
- Грунский И.С., Копытова О.М. О структуре контрольного эксперимента для определенно-диагностируемого автомата / И.С. Грунский, О.М. Копытова // Теория управляющих систем. – К.: Наук.думка, 1987. – С. 40-54.
- Грунский И.С., Копытова О.М. Неотличимость конечных автоматов в стационарной среде наблюдения / И.С. Грунский, О.М. Копытова // Дискретная математика. – 1993. – Т.5, вып.4. – С. 43-53.
- Копытова О.М. Неотличимость конечных автоматов кратными экспериментами в стационарной среде наблюдения / О.М. Копытова // Дискретная математика. – 1994. – Т.6, вып.2. – С. 120-128.
- Козловский В.А. О классе графов, порожденных локальными преобразованиями заданного графа / В.А. Козловский // Методы и системы технической диагностики. – Саратов: Изд-во Саратов. Ун-та. – 1985. – Вып.5. – С. 65-70.
- Копытова О.М. О структуре автоматов, сохраняющих
поведение при перебросках дуг / О.М. Копытова // Труды VIII Международной конференции
Дискретные модели в теории управляющих систем
(20.04 – 22.04.2015). Москва: Макс-Пресс, 2009. – С. 155-159. - Копытова О.М. Устойчивость автоматов к неисправностям их функции переходов / О.М. Копытова // Тр. ин-та ИПММ АН Украины. – 2010. – № 21. – С. 57-66.
- Бурлаева Е.И., Копытова О.М. Об одном типе локальных
преобразований автомата / Е.И. Бурлаева, О.М. Копытова // Материалы IV всеукраинской научно-технической
конфиренции студентов, аспирантов и молодых ученых
Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2013)
(24.04 – 25.04.2013). Донецк: ДонНТУ, 2013. – С. 479-484. - Копытова О.М. О возможности сохранения поведения автомата
при перебросках дуг / О.М. Копытова // Материалы VI Международной научно-практической конференции
Новости научной мысли – 2010
(27.10 – 05.11.2010), Чехия. Прага. Издательский домОбразование и наука
, 2010. – С. 41-46. - Швец О.С., Копытова О.М. О сравнении поведения ОДk-эталона
и автоматов, порождаемых его локальными преобразованиями / О.С. Швец, О.М. Копытова // Материалы
V всеукраинской научно-технической конференции студентов, аспирантов и молодых
ученых
Информационные управляющие системы и компьютерный мониторинг (ИУС КМ 2014)
(22.04 – 23.04.2014). Донецк: ДонНТУ, 2014. – С. 365-369.
