Аннотация
Койбаш А. А., Кривошеев С. В. Прогнозирование траектории движения подвижного объекта распределенного симулятора тяжелой инженерной техники. Выполнен анализ алгоритма поиска кратчайшего пути А* для подвижных объектов, исследовано применение архитектуры параллельных вычислений CUDA для прогнозирования. Проведен сравнительный анализ работы алгоритма на многоядерном процессоре и на GPU с использованием технологии CUDA.
Ключевые слова: прогнозирование поведения объекта, поиск кратчайшего пути, CUDA.
В настоящее время рост науки неизбежно приводит к внедрению новейших информационных разработок во многие сферы жизни. При помощи современных знаний происходят открытия новейших технологий, и значительную роль в этом играет моделирование. Одним из наиболее важных аспектов является предсказание поведения подвижных объектов с целью снижения влияния человеческого фактора. Для этого используется различные критерии, такие как вероятность определенного действия объекта, возможность выполнения какого-либо действия, а также характеристики действий и самого объекта. Есть множество способов описать схему поведения, и наиболее оптимальным является описание при помощи графов.
Наиболее рациональным является выполнение предсказания поведения объекта с помощью алгоритма А* – нахождение кратчайших путей полученного графа. Современные моделирования очень ресурсоёмки, поэтому важную роль играет и быстродействие. Для повышения эффективности вычислений необходимо распараллеливание процессов на GPU при помощи CUDA. В отличие от CPU, графические процессоры нацелены на максимальную многопоточность.
Задача алгоритма поиска А*состоит в том, что некий подвижный объект должен перейти из точки А в точку B по оптимальной траектории. Участок перемещения объекта содержит различные препятствия, которые необходимо обойти. Кроме этого, возможно добавление различных критериев (минимальный/максимальный угол поворота, ускорение/замедление и т.п.) для перемещения по прогнозируемой траектории.
Для решения этой задачи поле с максимально допустимой детализацией представляется в виде мультиграфа. При этом расстояние является весом ребра. Объект может ходить по горизонтали и вертикали, например, со стоимостью пути 10. Также возможно перемещение по диагонали, стоимость которого является 14 (корень из 102 + 102). Такое поле представлено на рис 1. Чем сильнее детализация поля, тем более точным будет проложенный путь.
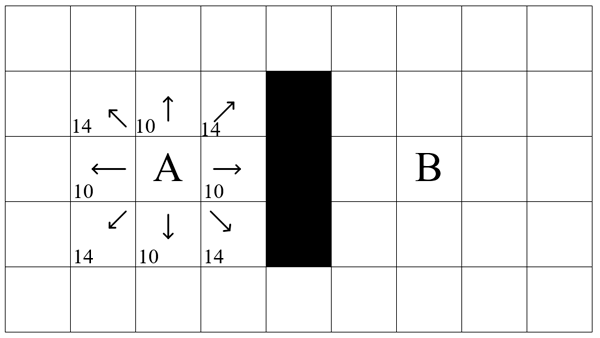
Рисунок 1 – Поле перемещения объекта
Поскольку исследуемым объектом является движущаяся техника, то самым рациональным является алгоритм Дейкстры, так как он наиболее оптимален при условии, что ребра не будут иметь отрицательного веса – нет убыточных движений [1]. Наилучшим решением для просчета кратчайшего пути является эвристический подход к алгоритму Дейкстры – алгоритм А*. В данном алгоритме пошагово просматриваются все пути, ведущие из вершины A в вершину B, пока не найдется путь с минимальной стоимостью.
Алгоритм реализуется следующими шагами:
- Формируются 2 списка вершин: уже рассмотренные вершины и ожидающие рассмотрения. В список рассмотренных заносится A.
- Для каждой соседней вершины производится расчет F = G + H, где G – стоимость пути от старта, а H – эвристическое приближение стоимости пути.
- Выбирается вершина с наименьшим F. Если она является B, то сохраняется путь, двигаясь от B назад к целевой точке. Иначе эта вершина выбирается текущей, удаляется из открытого списка и заносится в закрытый.
- Для каждой из точек, соседних с текущей, производятся следующие действия:
- Если соседняя точка уже рассмотрена, то она пропускается.
- Если соседней точки нет в списке ожидающих рассмотрения, то она добавляется в этот список. Текущая клетка для неё становится родительской. Рассчитывается F, G, H.
- Если соседняя клетка уже в списке ожидающих рассмотрения, то проверяется, не дешевле ли путь через эту клетку. Стоимость сравнивается по G. Если стоимость меньше, то родитель клетки меняется на текущую клетку и для неё пересчитываются стоимости G и F.
- Если список ожидающих рассмотрения пуст, а цели нет, то это означает, что маршрута до цели не существует.
Таким образом, алгоритм А* не только проведет движущийся объект беспрепятственно к цели, но и при этом обходит минимальное количество вершин, поскольку он эффективно использует эвристику.
С точки зрения аппаратных затрат данные вычисления являются ресурсоёмкими, т.к. необходимо учитывать множество факторов при прогнозировании траектории движения объекта. Для повышения быстродействия вычислений возможно применение не только многоядерного процессора CPU, но и графического процессора GPU.
Графический процессор GPU – это устройство, которое выполняет графическую обработку (рендеринг). Сегодня GPU эффективно применяется для обработки данных в компьютерной графике. Главной отличительной особенностью по сравнению с CPU является архитектура, максимально нацеленная на увеличение скорости расчёта.
Для графического просчета необходима параллельная обработка данных. GPU изначально мультипоточен. Архитектура спроектирована так, чтобы использовать большое количество нитей. Если современные CPU содержат несколько ядер (от 2 до 128), то в графическом процессоре количество ядер достигает несколько тысяч. Сравнительная схема CPU и GPU представлена на рис.2.
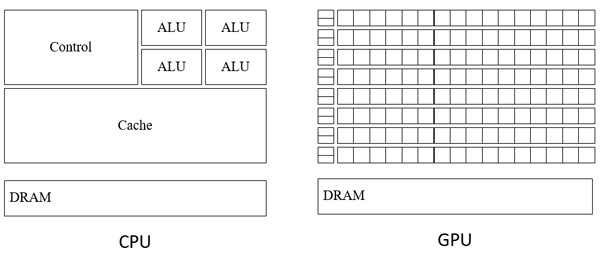
Рисунок 2 – Сравнительная схема CPU и GPU
CPU лучше работает с последовательными задачами. При большом объеме потоков информации преимущество имеет GPU. Для разработки программ, использующих GPU, применяется технология CUDA – программно-аппаратная архитектура параллельных вычислений от компании Nvidia. В технологию CUDA включен унифицированный шейдерный конвейер, позволяющий программе задействовать любое АЛУ в GPU [2]. Схема организации памяти программы CUDA отображена на рис. 3.
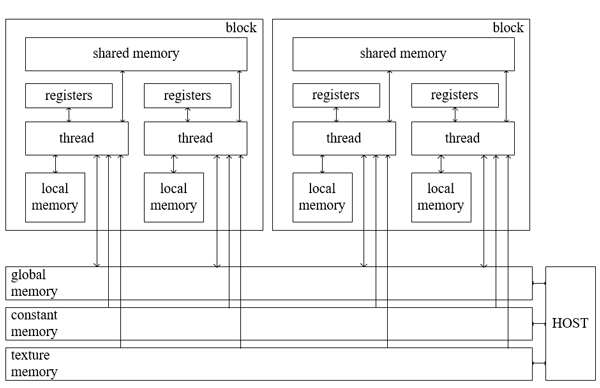
Рисунок 3 – Схема организации памяти CUDA-программы
Сравнение реализации алгоритма на CPU и на GPU показало, что для вычисления оптимальной траектории движения подвижного объекта более эффективно использовать графическую архитектуру. Использование библиотек CUDA дает возможность распараллелить процессы, тем самым увеличив производительность вычислений. Реализация данной программы на GPU также позволяет более точно вычислить траекторию, так как можно повысить интенсивность дискретизации поля.
Для прогнозирования оптимальной траектории движения был использован алгоритм А*, эффективно использующий эвристику. Во время исследования была проведена сравнительная характеристика вычисления алгоритма на многоядерном процессоре и на GPU, которая показала преимущества многопоточного вычисления этой задачи.
Список литературы
1. Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ – 3-е изд. – М.: «Вильямс», 2013. – С. 499–502.
2. Джейсон Сандерс, Эдвард Кэндрот Технология CUDA в примерах. Введение в программирование графических процессоров. – ДМК Пресс, 2011. – С. 20.