Аннотация
Койбаш А. А., Кривошеев С. В. Пути снижения времени прогнозирования траектории движения подвижного объекта распределенного симулятора тяжелой инженерной техники. Выполнен анализ особенностей алгоритма поиска кратчайшего пути А* для подвижных объектов, обоснована актуальность оптимизации вычисления маршрута при помощи средств управления потоками. Предложено несколько вариантов многопоточной реализации алгоритма. Проведен сравнительный анализ работы алгоритма для каждого метода распараллеливания на одном и нескольких ядрах разных процессоров, определены достоинства и недостатки каждого метода.
Ключевые слова: прогнозирование поведения объекта, поиск кратчайшего пути, многопоточность.
По мере развития техники совершенствуются средства передвижения и доставки. При этом маршрут зачастую не является кратчайшим, что приводит к лишним затратам времени и топлива. Сегодня информационные технологии интегрируются во все сферы человеческой деятельности, в связи с чем появляется возможность использовать передовые методы для оптимизации пути.
Существуют различные способы описания возможного поведения и выбора направления движущегося объекта, но самым оптимальным является описание схемы в виде мультиграфа, в котором расстояние принимается за вес рёбра, а перемещение между соседними вершинами возможно в горизонтальном, вертикальном и диагональном направлении. Для решения такого графа могут использоваться различные методы, однако в условиях передвижения и неотрицательного веса рёбер предпочтение отдаётся ускоренному алгоритму поиска пути А*, который представляет собой эвристический подход к алгоритму Дейкстры. Это подразумевает включение в расчёты оценочную стоимость – параметр, который задаёт вектор работы алгоритма. Благодаря этому алгоритм быстро находит путь при обходе наименьшего количества вершин.
Принцип алгоритма состоит в формировании закрытого и открытого списков, из которых выбирается текущая позиция. Для каждого такого положения просчитываются параметры 8 соседних вершин, после чего списки дополняются [1]. Пример обхода соседей вершины A проиллюстрирован на рисунке 1.
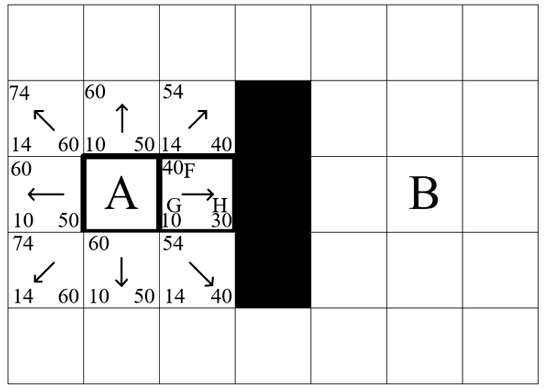
Рисунок 1 – Просчет параметров для соседних вершин
Для каждой вершины высчитывается стоимость пути:
F = G + H, (1)
где: G – стоимость передвижения к текущей вершине из начальной;
H – примерная стоимость передвижения от текущей вершины до конечной.
Следующей текущей вершиной становится соседняя с минимальным параметром F. При нахождении вершины B алгоритм выстраивает маршрут и завершает работу.
Реализация алгоритма играет важную роль. С повышением быстродействия возрастает производительность, что положительно сказывается не только на времени, но и на энергопотреблении и мощностных затратах выполнения просчета. Таким образом, можно гораздо быстрее просчитывать путь и улучшить детализацию маршрута, повышая уровень дискретизации рабочего поля.
Существенного повышения производительности можно добиться путем многопоточной реализации программы. В данном случае, алгоритм вынужден многократно производить последовательный обход 8 соседних вершин для каждой текущей позиции. Такие вычисления являются крайне ресурсоёмкими и по мере увеличения нагрузки, связанной с неудобным позиционированием маршрутных точек и препятствий, сильно возрастает время выполнения программы.
Для реализации алгоритма использован язык C#, так как платформа .NET предоставляет средства разработки и синхронизации многопоточных приложений, а также за счет компиляции исходного кода в байт-код CIL (Common Intermediate Language) с последующим исполнением виртуальной машиной даёт возможность создания кроссплатформенного приложения [2].
Одним из методов распараллеливания является распределение просчета одной или нескольких соседних вершин по разным потокам. Реализовано распределение на 2 потока, первый обрабатывает вершины 1 – 4, второй вершины 5 – 8. Другим вариантом является распараллеливание на 8 потоков, каждый из которых обрабатывает по одной соседней вершине. Оба варианта используют общие списки для потоков, поэтому для синхронизации обращения потоков к памяти используются мьютексы [3].
Для тестирования разработано поле со множеством препятствий и несколькими возможными маршрутами, чтобы усложнить работу для программы. Алгоритм проверялся на двух разных процессорах, поддерживающих многопоточность – Intel Core 2 Duo CPU 2.20 GHz, 2.20 GHz и Intel Pentium CPU B970 @ 2.30 GHz, 2.30 GHz. Однако тесты показали ухудшение производительности как на коротких интервалах, так и на длинных маршрутах. При распределении на 2 потока ухудшение быстродействия незначительно, однако 8-поточная реализация дала критическое падение производительности. Результаты теста показаны на рисунке 2.

Рисунок 2 – Диаграмма времени выполнения разных многопоточных реализаций
При помощи средств профилирования Microsoft Visual Studio 2013 сформирована статистика и определена конкуренция потоков за ресурсы [1]. Диаграмма конкуренции при реализации программы в 8 потоков представлена на рисунке 3.
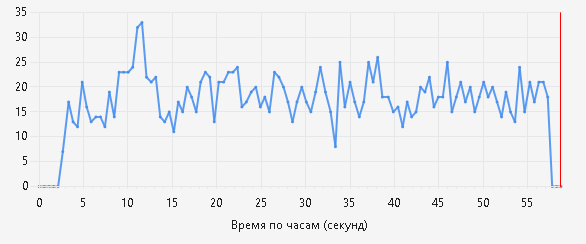
Рисунок 3 – Диаграмма конкуренции 8 потоков при просчете одного маршрута
Данная диаграмма отображает интенсивность конкуренции в секунду и показывает конфликты ресурсов. Повышенный уровень конкуренций негативно влияет на производительность, так как потоки простаивают в ожидании. Как видно из рисунка, частота конкуренции крайне высока - 33 состязания. Таким образом, метод распределения вершин по потокам имеет следующие недостатки: общий список осмотренных вершин, доступ к которому предоставляется синхронизацией мьютексами, что увеличивает задержку при одновременном обращении к одному участку памяти, а также синхронизация всех потоков в одном участке, при котором потоки ждут завершения друг друга. Данный недостаток возникает при каждом перемещении на соседнюю вершину, в связи с чем происходит серьёзное падение производительности.
Альтернативным вариантом является одновременный расчет пути сразу нескольких объектов. В этом случае задаются попарно несколько стартовых и конечных точек. При этом каждый поток имеет свой участок памяти – все переменные в функции являются локальными. Каждому маршруту соответствует свой поток, который формирует собственный список открытых и закрытых вершин. Для испытания такой реализации разработано несколько вариантов выполнения программы: для одного, двух, четырех и восьми маршрутов. Тестирования проведены на процессорах Intel Penuim CPU G2020 @ 2.90 GHz, 2.90 GHz и Intel Pentium CPU B970 @ 2.30 GHz, 2.30 GHz. Данный вариант показывает существенный прирост производительности – за одно и то же время просчитываются два и четыре маршрута. Результаты теста показаны на рисунке 4.
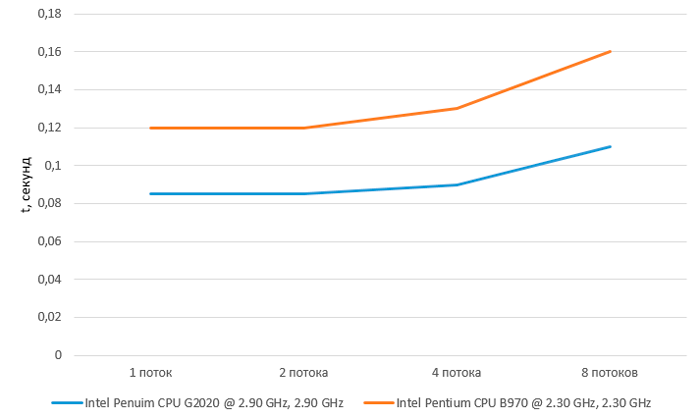
Рисунок 4 – Диаграмма времени выполнения разных многопоточных реализаций
Для двух потоков сформирована статистика и определена конкуренция потоков за ресурсы [1]. Диаграмма конкуренции отображена на рисунке 5.
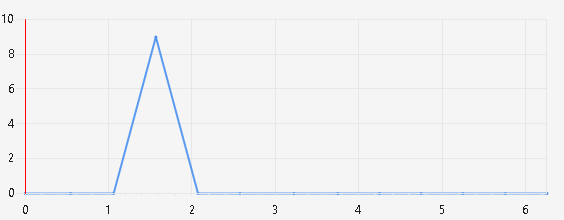
Рисунок 5 – Диаграмма конкуренции 2 потоков при просчете нескольких маршрутов
Конкуренция практически отсутствует, есть лишь состязания за синхронизацию в главном потоке. Существенный плюс данного варианта состоит в отсутствии разделяемой памяти и постоянного ожидания потоками друг друга в цикле.
Таким образом, при распараллеливании вычисления одного маршрута происходит падение производительности из-за синхронизации доступа к памяти и ожидания потоками завершения друг друга. Альтернативный вариант, при котором одновременно вычисляются несколько маршрутов, показывает улучшение производительности. Это связано с раздельной памятью и отсутствием необходимости ожидания потоков. Данный вариант можно комбинировать с методами декомпозиции одного маршрута на несколько участков, после чего выполнять мультипоточный расчет каждой части.
Список литературы
1. Койбаш А. А., Кривошеев С. В. Прогнозирование траектории движения подвижного объекта распределенного симулятора тяжелой инженерной техники. В кн.: Информатика, управляющие системы, математическое и компьютерное моделирование (ИУСМКМ – 2016): материалы VII междунар. науч.-техн. конф., Донецк, 2016. / редкол. А. Ю. Харитонов и др. Донецк: ДонНТУ, 2016. С. 343–346.
2. Кристиан Нейгел и др. C# 5.0 и платформа .NET 4.5 для профессионалов. – М.: «Диалектика», 2013. – 1440 с.
3. Hughes C., Hughes T. Professional Multicore Programming: Design and Implementation for C++ Developers. – Indianapolis: Wiley Publishing, Inc., 2008 – 648 p.