Автоматизированный коллоквиум как новая форма контроля знаний по графическим дисциплинам

Автор: Хейфец Александр Львович

Описание: Рассматривается новый подход в системе проверки геометро- графических знаний студентов.

Источник: http://www.ict.edu.ru/vconf/files/12120.pdf

Соавтор(ы): Хмарова Людмила Ивановна , Усманова Екатерина Александровна

Новая форма контроля знаний заключается в автоматической компьютерной проверке правильности построенных студентом модели или чертежа. Это существенно отличает новое направление от известных форм автоматизированного контроля, заключающихся в выборе правильного ответа из нескольких предложенных.

Новая форма контроля разработана на кафедре графики ЮУрГУ. Она внедрена [1] в учебный процесс в 2005 г. в виде автоматизированного коллоквиума применительно к комплексным задачам из курса начертательной геометрии.

Цель статьи – изложение существа нового метода контроля, обобщение опыта его внедрения.

Сущность автоматизированного коллоквиума состоит в следующем. Компьютер на экране генерирует исходные объекты геометрической задачи. Условия и параметры задачи формируются случайным образом. Студент решает задачу и в качестве ответа указывает построенные им объекты. Программа, заложенная в компьютер, проверяет параметры этих объектов и делает вывод о правильности или ошибочности решения.

Известно [2,3], что комплексные задачи активно формируют пространственное и логическое мышление у студентов. В них для определения искомого объекта необходимо выявить геометрические множества, которым этот объект должен принадлежать, а затем найти объект как общий элемент этих множеств.

На кафедре графики ЮУрГУ комплексным задачам уделяется должное внимание, совершенствуется методика их преподавания (в отличие от многих кафедр, которые в связи с сокращениями часов и сложностью этих задач исключили их из рабочих программ). Именно комплексные задачи были выбраны как первый объект приложения новой формы контроля знаний.

Переход на компьютерные 3d технологии в базовых графических дисциплинах, развиваемый на кафедре графики ЮУрГУ, отразился и на методике решения комплексных задач. Их на кафедре преподают по 3d, то есть на основе прямого моделирования пространственной моделью, без проекционных преобразований. Студенты с первого занятия осваивают AutoCAD, методы 3d моделирования в нем. Методика обучения AutoCAD’у за многие годы отработана и позволяет параллельно с изложением содержательной части курса нарабатывать в необходимом объеме и методы компьютерного моделирования. Курс начертательной геометрии трансформирован в курс теоретических основ геометрического моделирования, в котором начертательная геометрия является составной частью.

Автоматизированный коллоквиум выполнен как оболочка к пакету AutoCAD, созданная на языке AutoLisp [1,4]. AutoCAD рассматривается нами как базовый пакет для кафедр графики. Он позволяет с единой платформы решать задачи теоретического анализа, инженерной графики, дизайна, компьютерной графики, программирования и др.

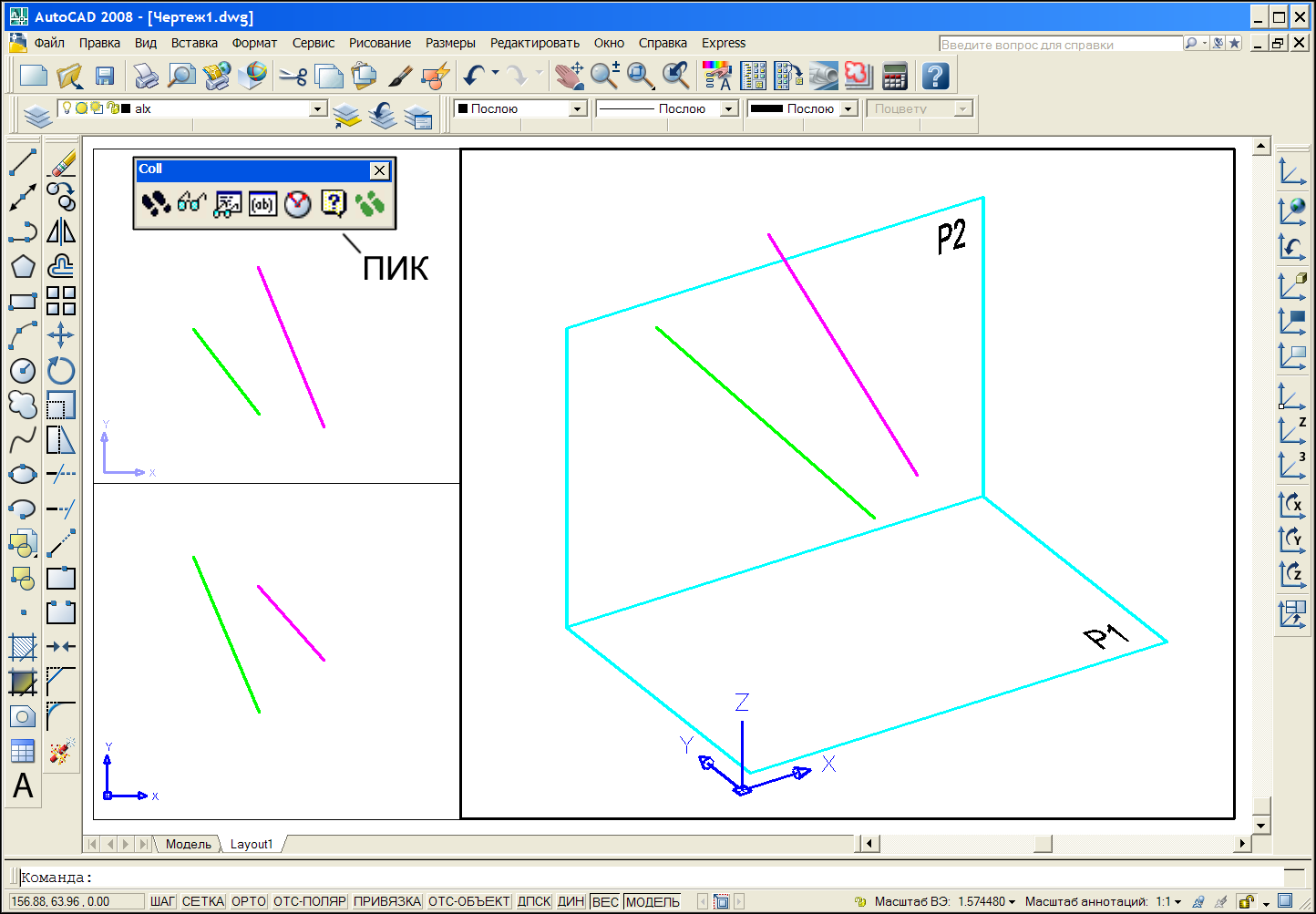
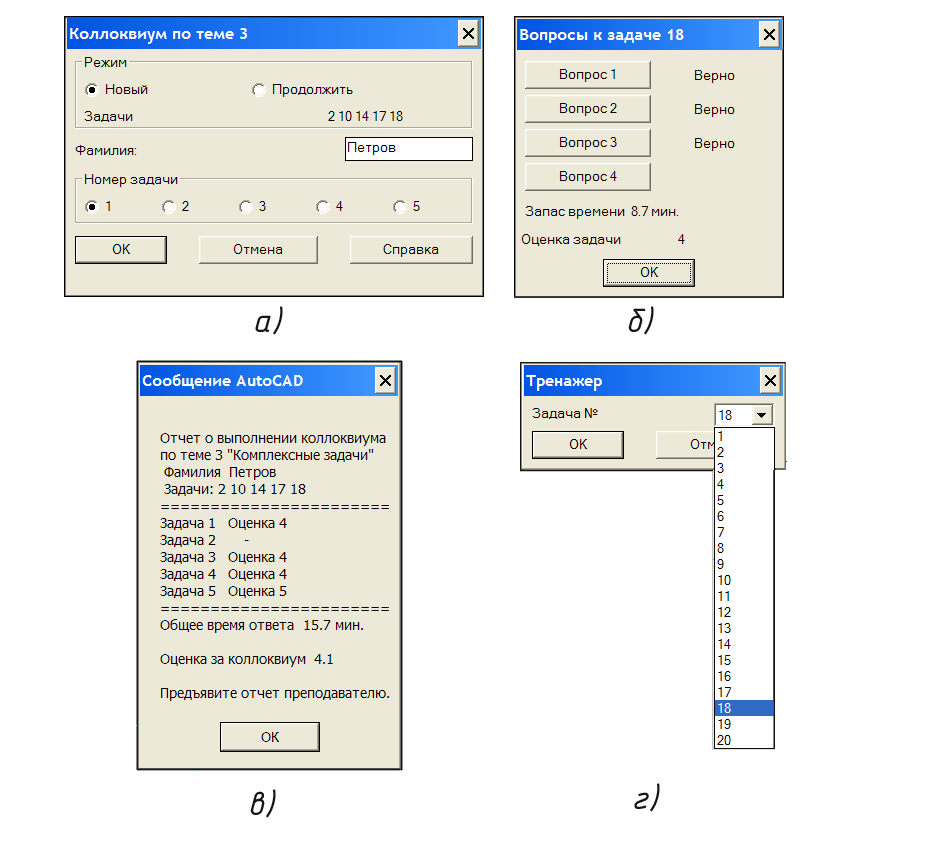
Работа с коллоквиумом происходит следующим образом. При его загрузке на экране возникает специальная панель инструментов коллоквиума (ПИК, рис. 1), содержащая семь кнопок. Далее по тексту статьи номера кнопок ПИК указаны по рис. 1 слева направо. При указании кнопки 1 возникает диалоговое окно (рис. 2, а), в котором студенту предложено зарегистрироваться. В том же окне выводятся номера пяти задач, предложенных компьютером для решения. Эти номера генерируются случайным образом из имеющегося набора задач. Студент выбирает задачу из предложенных – на экране возникают объекты, являющиеся ее исходными параметрами, и текст задачи. Геометрические объекты генерируются со случайными параметрами. Случайным образом назначаются и числовые параметры задачи, если они входят в условия. Объекты образуют 3d модель задачи. В процессе решения доступны все инструменты AutoCAD'а для 3d-построений. С момента генерирования условий начинается отсчет времени. На задачу выделяется 10 минут, за это время нужно ответить на четыре вопроса: первый – основной и последующие три дополнительные. Далее студент указывает кнопку 2 ПИК – возникает диалоговое окно (рис. 2, б), позволяющее вывести на экран вопрос и впоследствии проверить полученный ответ на этот вопрос.

Указав вопрос, студент приступает к решению. Ответ на каждый вопрос требует выполнения геометрических построений: нахождения отрезка, точки, окружности и др. Построив искомый объект, являющийся ответом на вопрос, студент указывает его курсором. Компьютер, “давно решив эту задачу”, сопоставляет предложенное студентом решение с контрольным. Решение должно быть предельно точным (допуск 0.001) и получено с применением известных методов точных построений. После указания объекта, являющегося ответом на вопрос, в том же окне возникает сообщение о правильности ответа или ошибке.

После правильного ответа на первый, основной вопрос задачи, становятся доступными еще три дополнительных вопроса. Студент вызывает эти вопросы, указывает построенные по ним объекты и получает дополнительные оценки. В том же окне приводится накапливаемая оценка за задачу, затраченное и оставшееся время.

Далее по кнопке 1 ПИК студент вызывает следующую задачу из тех, что компьютер предложил ему в начале коллоквиума, и выполняет ее решение в рассмотренной выше последовательности.

При указании кнопки 3 ПИК возникает диалоговое окно (рис. 2, в), в котором студент видит оценку за весь коллоквиум, накапливаемую по мере решения задач.

Экран с диалоговым окном (рис. 2, в), содержащим фамилию студента, “выпавшие” ему задачи, результат их решения, затраченное время и, в итоге, общую оценку за коллоквиум студент предъявляет преподавателю.

По кнопке 4 ПИК можно в любой момент повторно прочесть условия задачи. По кнопке 5 – контролировать затраченное и оставшееся время. По кнопке 6 выводится справочная информация по пользованию коллоквиумом.

Кнопка 7 (крайняя справа) вызывает “режим тренажера” (рис. 2, г), позволяющий при освоении коллоквиума сгенерировать любую его задачу.

На кафедре разработаны три коллоквиума. В первый включены задачи на построение прямых, параллельных или перпендикулярных заданным прямым или плоскостям, на построение скрещивающихся прямых, построение точек пересечения прямой с плоскостью или линии пересечения плоскостей. Ряд задач этого коллоквиума требует определить геометрическое место точек, равноудаленных от трех или четырех точек, или найти плоскость, равноудаленную от ближайших точек двух скрещивающихся прямых. Таким образом, этот коллоквиум обобщает весь материал, пройденный за первые два месяца обучения.

Второй коллоквиум ориентирован на нахождение геометрических множеств как поверхностей второго порядка. Третий – на частные случаи пересечения поверхностей второго порядка. Эти коллоквиумы даются позднее, не всем специальностям, в соответствии с их рабочей программой и изложением материала на лекции.

Остановимся на первом коллоквиуме, который дается всем специальностям и по которому имеется наибольший опыт внедрения. В качестве примера рассмотрим одну из его задач: “Заданы две скрещивающиеся прямые, зеленая и лиловая. Построить прямые, параллельные зеленой прямой, отстоящие от нее на заданное расстояние Δ и пересекающие лиловую прямую”.

После активизации задачи на экране возникают два отрезка, зеленый и лиловый, сгенерированные случайным образом (рис. 1). Экран состоит из трех видовых окон – это виды спереди, сверху и аксонометрия. В прототипе коллоквиума выполнены настройки, необходимые для выполнения 3d-построений. Значение Δ сгенерировано также случайным образом и приведено в тексте задачи, выведенном на экран.

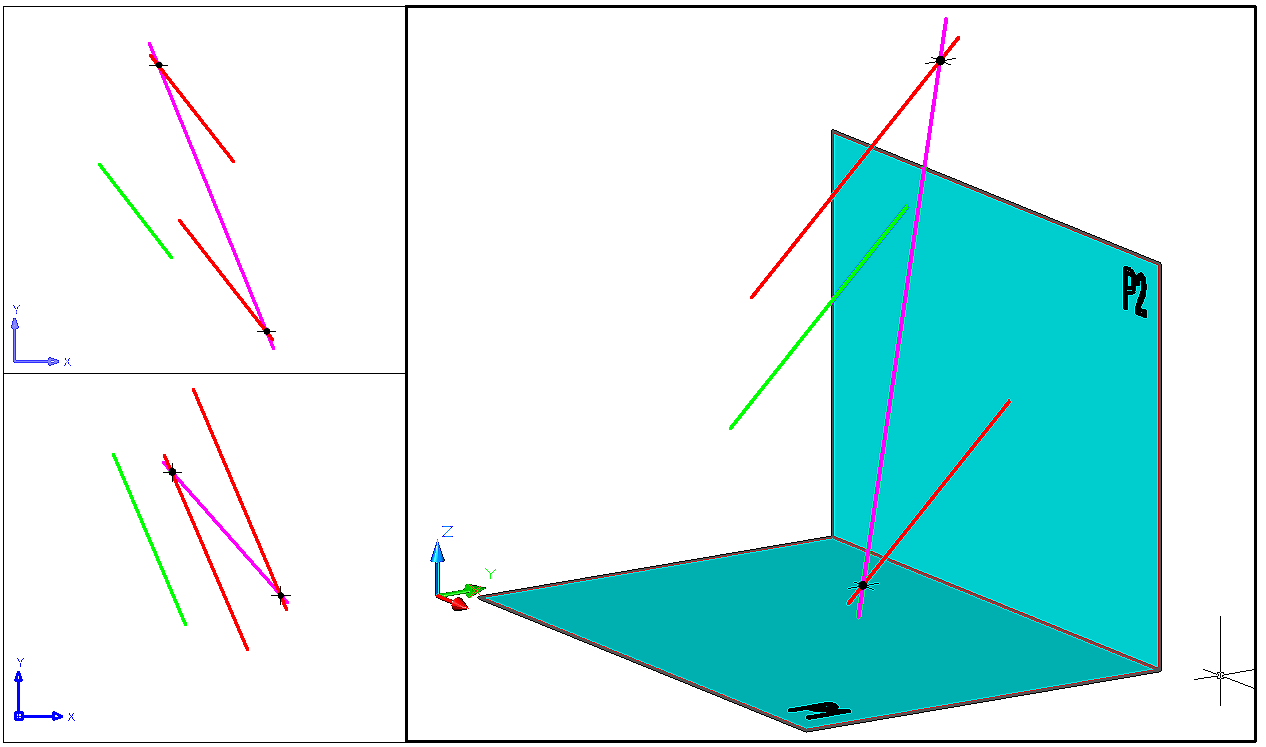
Из анализа задачи следует, что искомые прямые должны удовлетворять двум условиям. Первое – быть параллельными зеленой прямой и находиться от нее на расстоянии Δ. Второе – пересекать лиловую прямую. Из этого следует, что искомые прямые являются образующими цилиндрической поверхности радиуса Δ, осью которой является зеленая прямая. Искомые прямые должны также проходить через точки пересечения цилиндрической поверхности и лиловой прямой. По количеству точек пересечения делается вывод, что задача в общем случае имеет два решения, то есть две искомые прямые. Возможно также одно решение, возникающее, если прямая касается цилиндра. Если лиловая прямая не пресекает цилиндр, решение задачи отсутствует.

Алгоритм решения задачи, выбранный студентом, может быть различным: он зависит от его сообразительности, пространственного мышления и владения техникой пространственных построений на компьютере.

Правильное решение рассматриваемой задачи, получаемое студентом, приведено на рис. 3. Это два отрезка красного цвета.

В задаче имеются три дополнительных вопроса, основанных на правильном ответе на первый вопрос:

1. определите расстояние между точками пересечения найденных прямых с лиловой прямой;
2. определите угол между проекциями зеленой прямой на П1 и П2;
3. при каком расстоянии между зеленой и искомой прямыми задача имеет единственное решение.

Ответы на дополнительные вопросы требуют знания материала по всему курсу, пройденному к этому времени. В других задачах в дополнительные вопросы включено определение угла и кратчайшего расстояния между скрещивающимися прямыми, угла между плоскостями общего положения, построение проекций и следов, нахождение объемов, площадей, периметров центров тяжести и т. д.

Предусмотрено, что наиболее сложным в каждой задаче является последний четвертый вопрос. В данной задаче он требует от студента знания компьютерного 3d алгоритма определения кратчайшего расстояния между скрещивающимися прямыми [3,4].

Разработан программный алгоритм простановки оценки за задачу и за коллоквиум. Он учитывает количество правильных ответов на вопросы по каждой задаче, количество решенных задач и затраченное время. На вопросы, предложенные в задаче, можно отвечать многократно, добиваясь правильного ответа.

За время коллоквиума можно “перерешивать” задачи, добиваясь более высокой оценки. В этом случае условия задачи качественно остаются неизменными (то есть компьютер не позволяет выбрать другую задачу), но каждый раз она генерируется с новыми параметрами. Превышение допустимого времени, выделяемого на решение задачи (10 мин.), приводит к снижению оценки на 0.5 балла.

Диапазон оценок вполне лоялен. Так, для “тройки” за задачу достаточно ответить только на ее первый вопрос. Для “тройки” за коллоквиум достаточно получить “тройки” по трем задачам из пяти. Отличная оценка требует полного ответа на все вопросы по всем задачам.

По усмотрению преподавателя алгоритм оценки может быть ужесточен. Разработка алгоритма оценки – это интересная педагогическая задача.

Составление программ [1] для коллоквиума требует знания основ программирования на языке AutoLisp. Созданная за прошедшее время оболочка, библиотека вспомогательных функций (подпрограмм) и наработанная методика позволяют преподавателям создавать программы после 3-4 месяцев подготовки.

Коллоквиум выдается студентам в ноябре. К этому времени они уже владеют техникой пространственных построений в AutoCAD’е, который изучают с первого сентября. Объяснения по задачам коллоквиума даются на одном-двух практических занятиях. Учитывая, что условия задач генерируются случайным образом, исключающим формальное запоминание решения, файл коллоквиума сразу же выдается студентам на дом для освоения. Защита коллоквиума происходит на занятии в компьютерном классе. На выполнение всех пяти задач коллоквиума выделяется 45 минут. Для ряда специальностей коллоквиум дается в объеме 1-2 задач на экзамене как один из вопросов экзаменационного билета.

50…70% студентов сдают коллоквиум с первого раза. Остальным предоставляется еще одна попытка сдать коллоквиум на занятии. Для оставшихся 5...7% защита переносится на дополнительные занятия, как правило, на коммерческой основе.

Первоначально коллоквиум содержал пять задач. У преподавателей постоянно возникали сомнения в том, что студенты запоминают решение. Тогда количество задач в коллоквиуме было увеличено до десяти, а в последний год доведено до двадцати. Ведется работа по дальнейшему расширению количества задач. Сложно предположить, что студенты запоминают решение такого количества задач, каждая из которых еще содержит по три, как правило, оригинальных дополнительных вопроса. Где в таком случае граница между пониманием и запоминанием? Даже если слабые студенты запоминают решение, в таком объеме этого вполне достаточно для положительной оценки. В этом направлении требуются педагогические исследования.

Опыт внедрения автоматизированного коллоквиума показал, что он вызывает несомненный интерес у студентов. Это как творческий интерес, так и нормальный “детский”. Достаточно отметить стихийно возникающие в группах соревнования на скорость выполнения коллоквиума на отличную оценку.

На кафедре графики ЮУрГУ ведется работа по расширению новой формы контроля применительно к проверке заданий по инженерной графике, то есть автоматизированной проверке моделей и чертежей деталей. Это научное-методическое направление, соответствующее современным направлениям в технике построения чертежа, тенденциям повышения самостоятельности в работе студентов и развития дистанционных форм обучения.

Выводы:

1. Новая форма контроля знаний по графическим дисциплинам, основанная на проверке правильности графического решения студента, а не на выборе им правильного ответа из ряда предложенных, несомненно, является перспективной;
2. В рамках нового направления энергия преподавателя направлена не на то, как ввести студента в заблуждение неправильными ответами, а на разработку интересных задач и составление программ их реализации.

 

Графические материалы