УДК 004.942

Исследование программных моделей нейронных сетей прямого распространения

Авторы: Медгаус С.В., Федяев О.И.

Источник: Информатика, управляющие системы, математическое и компьютерное моделирование в рамках III форума «Инновационные перспективы Донбасса» (ИУСМКМ – 2017): VIII Международная научно-техническая конференция, 25 мая 2017, г. Донецк: / Донец. национал. техн. ун-т; редкол. Ю.К. Орлов и др. – Донецк: ДонНТУ, 2017. – 802 с. с. 181 – 187. [ссылка на сборник]

Аннотация: В данной статье рассмотрены наиболее распространённые стратегий обучения нейронных сетей прямого распространения, а также приведены программные модели нейросетей, для которых применены эти алгоритмы и приведён анализ их эффективности.

Введение

Многие задачи, которые решаются в настоящее время с помощью компьютерных систем, с точки зрения формализма разработки алгоритма решения, относятся к классу трудно формализуемым (а иногда и к неформализуемым) задачам. Для них невозможно чётко определить логику функционирования программы для решения поставленной задачи. К таким задачам относятся задачи распознавания и классификации образов, сжатия данных, идентификации и управления сложными объектами, аппроксимации и интерполяции, прогнозирования динамики процессов и т. д. [1]. Для решения таких задач стали успешно применять искусственные нейронные сети благодаря их способности к обучению и к обобщению полученных знаний. В настоящее время разработано много типов нейронных сетей для указанного класса прикладных задач.

Среди множества существующих типов сетей в качестве важнейших можно выделить нейронные сети прямого распространения (с прямой связью). Согласно теоретическим результатам нейронные сети с прямой связью и с сигмоидальными функциями активации являются универсальным средством для приближения (аппроксимации) произвольных функций. Однако нет никакого правила, позволяющего найти оптимальную топологию сети для решаемой задачи. Таким образом, задача построения адекватной нейронной сети является нетривиальной. Вопросы о том, сколько нужно взять скрытых слоёв, сколько нейронов в каждом из них, какие связи, в имеющейся литературе, как правило, трактуются бездоказательно и предлагаются решать путём простого перебора различных архитектур.

Другая проблема связана с правильной организацией процесса обучения нейронной сети [2]. Насколько качественно он будет организован, зависит способность сети решать поставленные перед ней задачи во время штатного функционирования. Ключевым вопросом в обучении является выбор алгоритма настройки нейросети. Все подобные алгоритмы основаны на методах оптимизации нелинейной многомерной функции ошибки, поэтому длительность процесса обучения и его качество зависит не только от применяемого метода оптимизации, но и от других факторов (особенностей структуры нейросети, обучающего множества). Разработано уже более сотни разных обучающих алгоритмов, отличающихся друг от друга стратегией оптимизации и критерием ошибок. Для задачи многомерной оптимизации предложен большой спектр методов, начиная от градиентного метода наискорейшего спуска и заканчивая методом Монте-Карло и генетическими алгоритмами.

Описанные проблемы приводят к тому, что при практической работе с нейронными сетями прямого распространения приходится экспериментировать с большим числом различных сетей, порой обучая каждую из них по нескольку раз и сравнивая полученные результаты. Главным показателем качества результата является здесь контрольная ошибка. При этом, в соответствии с общесистемным принципом, из двух сетей с приблизительно равными ошибками контроля имеет смысл выбрать ту, которая проще.

Несмотря на значительное количество уже известных практических приложений нейросетей прямого распространения, возможности их дальнейшего использования для обработки сигналов не изучены окончательно. Поэтому цель данной научной работы состоит в разработке программных моделей нейросетей прямого распространения и исследовании их ключевых свойств (представления и обучения) для разработки на их основе качественных программных агентов с нейросетевой архитектурой. Для этого рассмотрены две типовые структуры сетей прямого распространения и алгоритмы их обучения по стратегии обучение с учителем.

1 Однослойная сеть прямого распространения (однослойный персептрон)

Типовая структура однослойного персептрона, ориентированная на решение задачи распознавания графических символов показана на рис. 1.

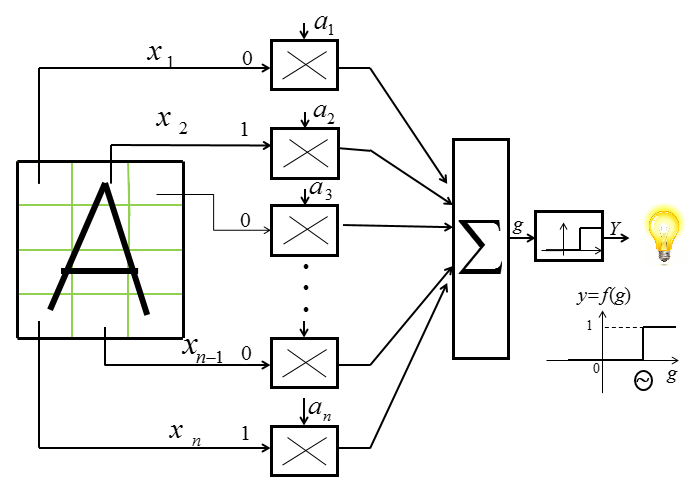
Для обучения нейросети применялась стратегии контролируемого обучения: учитель подаёт на вход сети оцифрованный образ буквы, а на выход сообщает желаемое значение результата распознавания (буква гласная или согласная). Такой набор контрольных примеров был сгруппирован в обучающее множество {(X,Y)}. В ходе обучения по алгоритму дельта-правило вычисляется ошибка δ (дельта), как разность между требуемым сигналом и фактическим выходом.

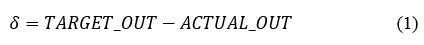
Полученная ошибка служит основой для корректировки весов нейрона. После получения значения ошибки для каждого из нейронов (если их несколько в слое) вычисляется значение новых весов на основании этой ошибки и параметра скорости обучения (2).

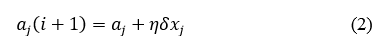
где
i – номер текущей итерации (эпохи) обучения персептрона;
j – номер синаптической связи;
η – коэффициент скорости обучения, позволяет управлять средней величиной изменения весов (0 < η <1);
x_j – величина входа соответствующая a_j синаптическому весу.

Сходимость алгоритма (1 – 2) исследовал Ф. Розенблатт [3], а также другие авторы в более поздних публикациях. Данный алгоритм обучения хороший, но он применим только для однослойных нейросетей, в которых ошибка непосредственно влияет на единственные веса, ведущие ко входам в нейронной сети [2].

Для исследования данной нейросети была разработана её программная модель, которая реализует один нейрон с одним выходом и многими входами с соответствующими весовыми коэффициентами [3] (см. рис. 1). В обучающее множество включены изображения первых 10 букв с разным начертанием и задан признак гласности каждой из букв. После этого НС была обучена по рассмотренному алгоритму на данных примерах с приемлемым уровнем точности (до 100% распознавания) (см. рис. 2).

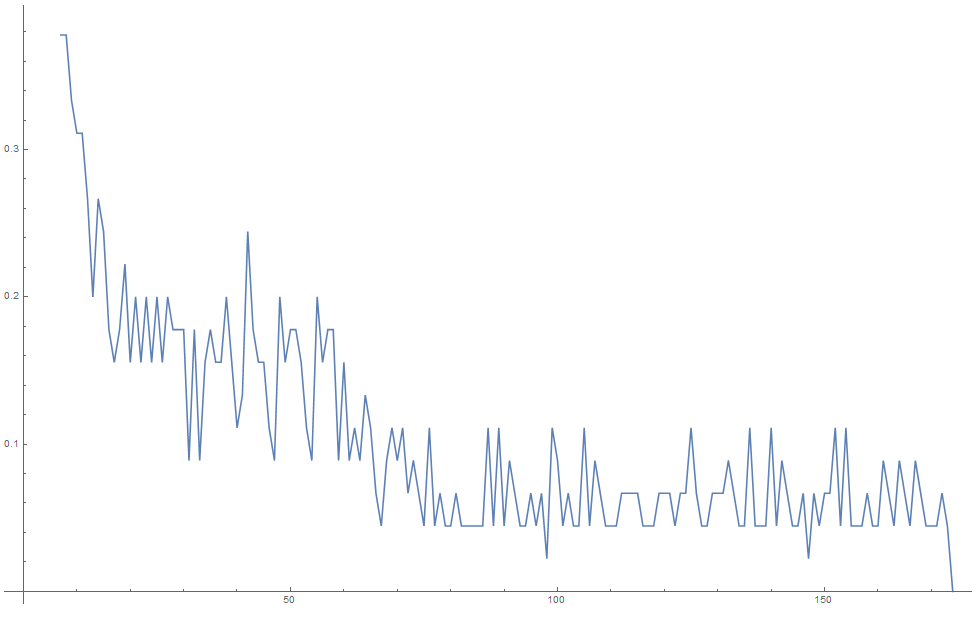
При тестировании программной модели нейросети на её вход подавались новые образы букв, незнакомые системе, и система выдавала в 80% правильные результаты распознавания (см. рис. 3 - 4).

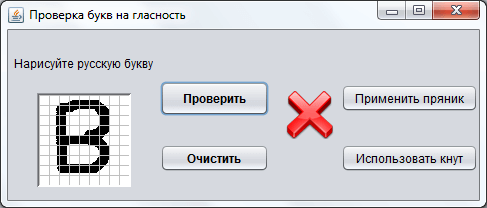
Также разработанная программная модель позволяет дообучать нейросеть с новыми образами, для этого пользователю необходимо нарисовать новый образ и запустить проверку. Если система выдаёт правильный результат, то одобрить её вычисления. Иначе нужно пожурить её, чтобы в следующий раз при обучении она не делала неправильных вычислений.

2 Многослойная сеть прямого распространения (многослойный персептрон)

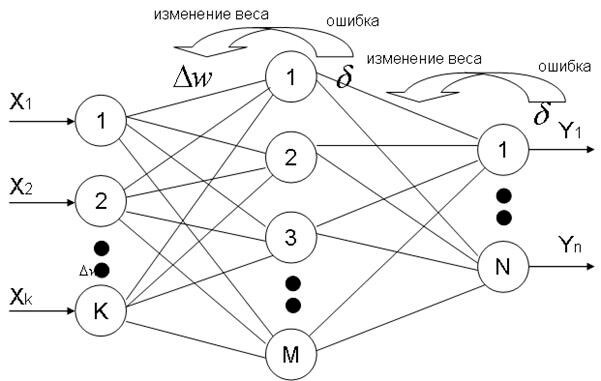
Для обучения многослойных нейронных сетей был программно реализован эффективный алгоритм обратного распространения ошибки (Backpropagation), представляющий собой развитие обобщённого дельта-правила [4, 5]. Этот алгоритм считается наиболее известным и чаще всего применяемым в искусственных нейронных сетях прямого распространения. Эта стратегия обучения применима как для однослойных, так и для многослойных НС. Ошибка из выходного слоя НС последовательно распределяется и передаётся внутренним скрытым слоям, в итоге достигая первого скрытого слоя [4]. Основные действия при обратном распространении ошибки представлены на рис. 5 [5].

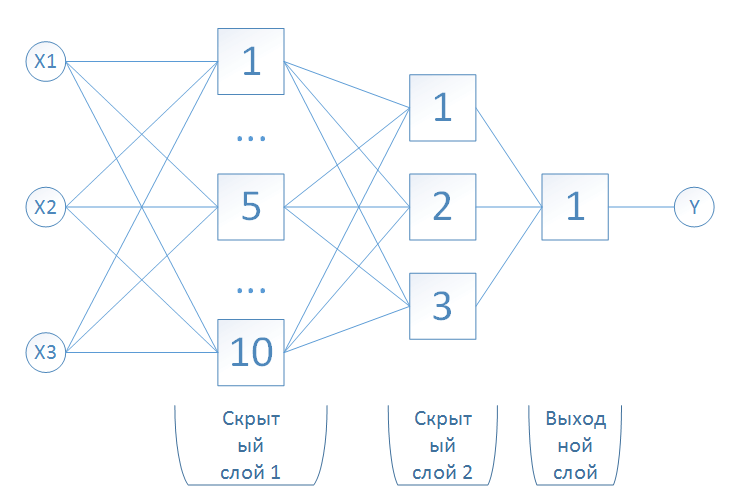
Для исследования этого типа нейросети также была разработана программная модель. Структура многослойной нейросети показана на рис. 6. Она представляет собой трёхслойную НС, которая использует для обучения алгоритм обратного распространения ошибки. Качество данной нейросети оценивалось на решении задачи прогнозирования динамического процесса.

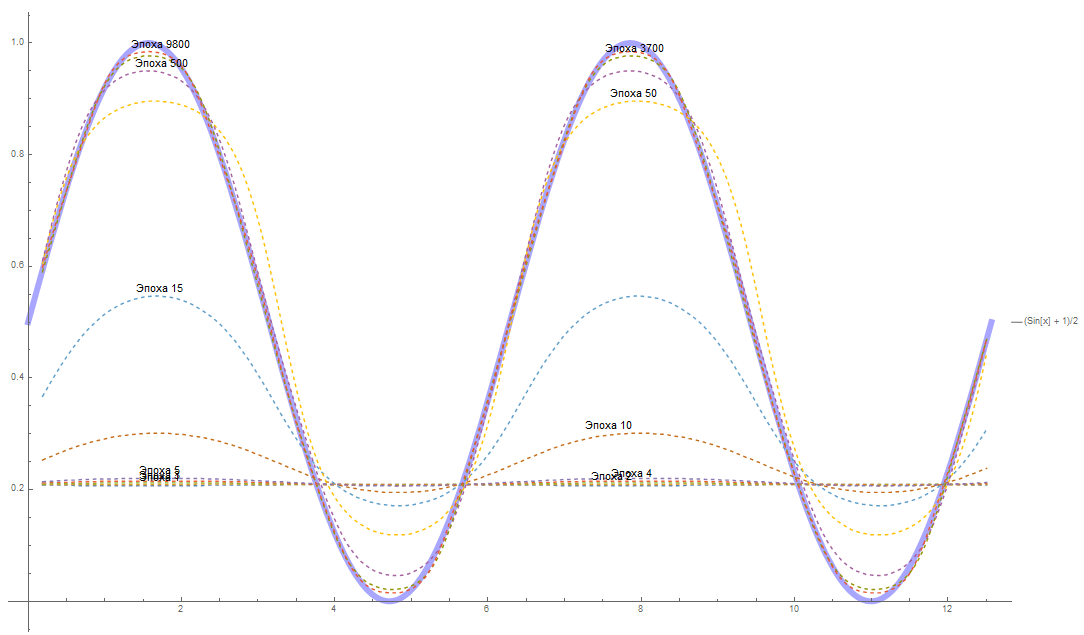
Динамика процесса описывалась синусоидальной функцией. В эксперименте использовалась функция sin(x). Для обучения НС функция была разбита на отрезки и с помощью метода окон (Windowing) было построено обучающее множество [6]. При обучении была достигнута ошибка в 0.005%. С целью ускорения процесса обучения сети предложены многочисленные модификации алгоритма обратного распространения ошибки, связанные с использованием различных функций ошибки, процедур определения направления и величины шага.

На рис. 7 представлена динамика обучения нейронной сети в зависимости от количества эпох обучения.

Выводы

В ходе исследования были проанализированы различные структуры нейронных сетей и методы их обучения. Также были разработаны программные модели вышеуказанных нейросетей с целью проведения экспериментов по анализу их эффективности.

В результате был подтверждён тезис о способности нейросетей распознавать образы и выявлены основные достоинства и недостатки различных алгоритмов обучения нейросетей прямого распространения.

Литература

1. Искусственные нейронные сети [электронный ресурс]. – Режим доступа: https://neuralnet.info/chapter/введение/
2. Алгоритм обучения НС прямого распространения по дельта-правилу [электронный ресурс]. – Режим доступа: http://www.aiportal.ru/articles/neural-networks/perceptron-learning.html
3. Структура персепетрона [электронный ресурс]. – Режим доступа: https://neuralnet.info/chapter/основы-инс/
4. Алгоритм обратного распространения ошибки в многослойных НС [электронный ресурс]. – Режим доступа: http://www.gotai.net/documents/doc-nn-009-06.aspx
5. Основные действия при обратном распространении ошибки [электронный ресурс]. – Режим доступа: http://apsheronsk.bozo.ru/Neural/Lec3.files/image030.jpg
6. Метод плавающего окна [электронный ресурс]. – Режим доступа: http://masters.donntu.ru/2006/kita/kiryan/library/art06.htm