Русский   English
ДонНТУ   Портал магістрів

Реферат по темі Дослідження і розробка методу визначення об'єкта на зображенні з допомогою алгоритму мурашиних колоній

Зміст

                    

ВСТУП

        

В останні роки інтенсивно розробляється науковий напрямок з назвою Природні обчислення (Natural Computing), що об'єднує математичні методи, в яких закладені принципи природних механізмів прийняття рішень. Ці механізми забезпечують ефективну адаптацію флори і фауни до навколишнього середовища на протязі декількох мільйонів років.

        

Серед так званих Soft computing techniques, розроблених за останні десять років для важко вирішуваних задач дискретної оптимізації, числяться:

        

Імітація самоорганізації мурашиної колонії складає основу мурашиних алгоритмів оптимізації. колонія мурах може розглядатися як багатоагентна система, в якій кожен агент (мураха) функціонує автономно по дуже простим правилам. На противагу майже примітивного поведінки агентів, поведінка всієї системи виходить напрочуд розумним.

        

Мурашині алгоритми серйозно досліджуються європейськими вченими з середини 90-х років. На сьогоднішній день вже отримані хороші результати для оптимізації таких складних комбінаторних задач, як задача комівояжера, задача оптимізації маршрутів вантажівок, завдання розмальовки графа, квадратична задача про призначення, завдання оптимізації мережевих графіків, завдання календарного планування і багато інших. Особливо ефективні мурашині алгоритми при динамічної оптимізації процесів в розподілених нестаціонарних системах, наприклад, трафіків в телекомунікаційних мережах.

                 

1. ПОСТАНОВКА ЗАДАЧІ

Метою магістерської дисертаційної роботи є дослідження і розробка методу визначення об'єкта на зображенні за допомогою алгоритму мурашиних колоній.

        

Для досягнення даної мети необхідно виконати ці завдання:

        
                
  1. Проаналізувати сучасний стан проблеми визначення об'єктів на зображенні.
    2.             
  2. Проаналізувати сучасні методи ройовий оптимізації детектування об'єктів на зображенні.
    3.             
  3. Розробити ройовий метод визначення об'єктів на зображенні за допомогою алгоритму мурашиних колоній.
    4.             
  4. Запропонувати модифікацію ройового алгоритму, для оптимізації алгоритму мурашиних колоній для визначення об'єкта на зображенні.
    5.             
  5. Розробка програмного забезпечення, ройового алгоритму, для оптимізації алгоритму мурашиних колоній і проведення його тестування.
    6.             
  6. Проведення порівняння ефективності розробленого ройового алгоритму з існуючим алгоритмом.
                 

2. ОГЛЯД СУЧАСНОГО СТАНУ ПРОБЛЕМИ

Розглянемо основні наукові роботи пов'язані з дослідженням можливості використання алгоритму мурашиних колоній для обробки зображень:

У роботі "Ant Colony Optimization towards Image Processing" K. Kavita, A. Madan розглядаються різні завдання обробки зображень, які можуть бути досягнуті за допомогою оптимізації алгоритму мурашиних колоній - важлива область м'яких обчислень. Алгоритм мурашиних колоній, є підхід, заснований на обчислювальному інтелекті, який використовується для вирішення комбінаторних проблема оптимізації. Простота і оптимальний підхід алгоритму мурашиних колоній привела до його застосовності до маршрутизації, планування, проблеми з підмножиною, завданням і класифікацією. Виявлення краю, прив'язка до країв, витяг функції, сегментація і стиснення зображень - це різні завдання обробки зображень, в яких алгоритм успішно застосовується.

У роботі "An application of ant colony optimization to image clustering" T. Piatrik, E. Izquerto розглядається можливість кластеризації зображення за допомогою оптимізації алгоритму мурашиних колоній. Автори прийшли до того, що вихідний пошук зображень може бути значно покращено за рахунок забезпечення гарної первісної кластеризації візуальних даних. Проблема кластеризації зображень полягає в тому, що більшість сучасних алгоритмів не можуть ідентифікувати окремі кластери, що існують в різних підпросторах ознак. У даній статті пропонується новий підхід для кластеризації підпросторів на основі оптимізації колоній мурашок і механізму навчання. Пропонований алгоритм змінює припущення про те, що все кластери в наборі даних знаходяться в одному наборі вимірювань, привласнюючи ваги функцій відповідно до локальних корреляциями даних уздовж кожного виміру. Результати експериментів з наборами даних реальних зображень показують необхідність вибору функцій в кластеризації і переваг вибору функцій локально.

У роботі "A Novel Image Segmentation Algorithm Based on Artificial Ant Colonies" Huizhi Cao, Peng Huang, and Shuqian Luo представлений новий алгоритм сегментації, в якому використовується біологічно натхненна парадигма, відома як колонії штучних мурах. З огляду на особливості колоній штучних мурах, використовується розширена модель, що застосовується при сегментації зображення. Кожна мураха в моделі наділений здатністю запам'ятовувати контрольний об'єкт, який буде оновлюватися при виявленні нової мети. Міра нечіткої зв'язності приймається для оцінки подібності між цільовим об'єктом і еталонним об'єктом. Поведінка одного мурашки залежить від сусідніх мурах, і співпраця між мурахами здійснюється шляхом обміну інформацією за допомогою оновлення феромонів. Моделюються результати показують ефективність нового алгоритму, який здатний зберігати деталі об'єкта і нечутливий до шуму.

В работе “Image Feature Selection Based on Ant Colony Optimization” Ling Chen, Bolun Chen, Yixin Chen представляется алгоритм выбора признаков, основанный на оптимизации колонии муравьев (ACO). Для n функций большинство методов выбора объектов на основе ACO используют полный граф с ребрами O (n2). Однако искусственные муравьи в предлагаемом алгоритме пересекаются на орграфе с только 2n дугами. Алгоритм использует производительность классификатора и количество выбранных функций как эвристическую информацию и выбирает оптимальное подмножество функций с точки зрения размера набора функций и эффективности классификации. Экспериментальные результаты на разных изображениях показывают, что алгоритм может получить лучшую точность классификации с меньшим набором функций по сравнению с другими алгоритмами.

                 

3. СУЧАСНI МЕТОДИ РОЇВ ОПТИМІЗАЦІЇ ДЕТЕКТУВАННЯ ОБ'ЄКТІВ НА ЗОБРАЖЕННІ

3.1 Мурашний алгоритм

        

Мурахи відносяться до соціальних комах, що створює колективи. Колективна система здатна вирішувати складні динамічні завдання з виконання спільної роботи, яка не могла б виконуватися кожним елементом системи в окремо в різноманітних середовищах без зовнішнього управління, контролю або координації. У таких випадках говорять про ройовий інтелект (Swarm intelligence), як про хитромудрих способи кооперативного поведінки, тобто стратегії виживання.

        

Одним з підтверджень оптимальності поведінки мурашиних колоній є той факт, що мережа гнізд суперколоній 

близька до мінімального остовного дерева графа їх мурашників.

  

Основу поведінки мурашиної колонії становить самоорганізація, що забезпечує досягнення загальних цілей колонії на основі низкоуровневого взаємодії. Колонія не має централізованого управління, і її особливостями є обмін локальної інформацією тільки між окремими особинами (прямий обмін - їжа, візуальні і хімічні контакти) і наявність непрямого обміну, який і використовується в мурашиних алгоритмах. Таким чином, в загальному випадку розглядаються сліпі мурахи, не здатні відчувати близькість їжі.

        

Непрямий обмін - стігмержі (stigmergy), являє собою рознесенихе в часі взаємодія, при якому одна особина змінює деяку область навколишнього середовища, а інші використовують цю інформацію пізніше, коли в неї потрапляють. Біологи встановили, що таке відкладене взаємодія відбувається через спеціальне хімічна речовина - феромон (pheromone), секрет спеціальних залоз, відкладається при переміщенні мурашки. Концентрація феромону на шляху визначає перевагу руху по ньому.

Мурашині алгоритми являють собою імовірнісну жадібну евристику, де ймовірності встановлюються, виходячи з інформації про якість рішення, отриманої з попередніх рішень. Вони можуть використовуватися як для статичних, так і для динамічних комбінаторних оптимізаційних задач. Збіжність гарантована, тобто в будь-якому випадку ми отримаємо оптимальне рішення, однак швидкість збіжності невідома.

3.2 Історія створення мурашиних алгоритмів

Почалося все з вивчення поведінки реальних мурах. Експерименти з Argentine ants, що проводяться Госсом в 1989 і Денеборгом в 1990 році послужили відправною точкою для подальшого дослідження ройового інтелекту. Дослідження застосування отриманих знань для дискретної математики почалися на початку 90-х років XX століття, автором ідеї є Марко Дориго з Університету Брюсселя, Бельгія. Саме він вперше зумів формалізувати поведінку мурах і застосувати стратегію їхньої поведінки для вирішення завдання про найкоротших шляхах. Пізніше за участю Гамбарделло, Тайлларда і Ді Каро були розроблені і багато інших підходи до вирішення складних оптимізаційних задач при допомогою мурашиних алгоритмів. На сьогоднішній день ці методи є досить конкурентоспроможними порівняно з іншими евристиками і для деяких завдань дають найкращі на сьогоднішній день результати.

3.3 Концепція мурашиних алгоритмів

Ідея мурашиного алгоритму - моделювання поведінки мурах, пов'язаного з їх здатністю швидко знаходити найкоротший шлях від мурашника до джерела їжі і адаптуватися до умов, що змінюються, знаходячи новий найкоротший шлях. При своєму русі мураха мітить шлях феромоном, і ця інформація використовується іншими мурахами для вибору шляху. Це елементарне правило поведінки і визначає здатність мурах знаходити новий шлях, якщо старий виявляється недоступним.

Розглянемо випадок, показаний на малюнку, коли на оптимальному досі шляху виникає перешкода. В цьому випадку необхідно визначення нового оптимального шляху. Дійшовши до перепони, мурахи з однаковою ймовірністю будуть обходити її справа і зліва. Те ж саме буде відбуватися і на зворотному боці перешкоди. Однак, ті мурахи, які випадково виберуть найкоротший шлях, будуть швидше його проходити, і за кілька пересувань він буде більш збагачений феромонами. Оскільки рух мурах визначається концентрацією феромону, то наступні будуть віддавати перевагу саме цей шлях, продовжуючи збагачувати його феромоном доти, поки цей шлях з якої-небудь причини не стане недоступний.

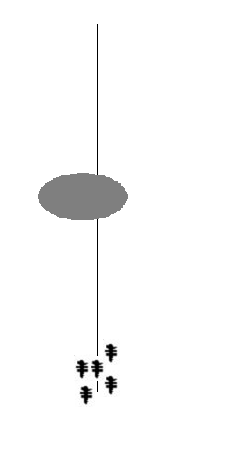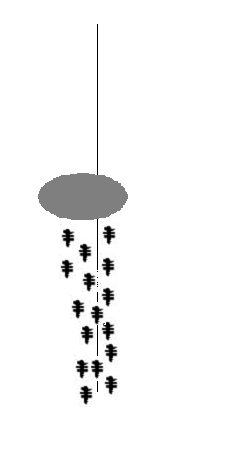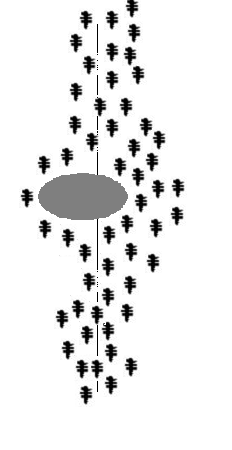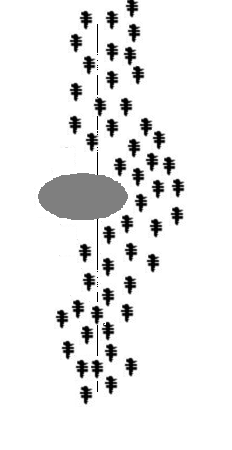
anim.gif

Маршрут руху мурахiв

Очевидна позитивний зворотний зв'язок швидко призведе до того, що найкоротший шлях стане єдиним маршрутом руху більшості мурашок. Моделювання випаровування феромону - негативного зворотного зв'язку - гарантує нам, що знайдене локально оптимальне рішення не буде єдиним - мурашки будуть шукати й інші шляхи. Якщо ми моделюємо процес такої поведінки на деякому графі, ребра якого являють собою можливі шляхи переміщення мурашок, протягом певного часу, то найбільш збагачений феромонами шлях по ребрах цього графа і буде рішенням завдання, отриманим за допомогою мурашиного алгоритму.

3.4 Узагальнений алгоритм

Будь-мурашиний алгоритм, незалежно від модифікацій, уявімо в наступному вигляді:

Тепер розглянемо кожен крок в циклі більш докладно:
  1. Створюємо мурах.
    • Стартова точка, куди поміщається мураха, залежить від обмежень, що накладаються умовами завдання. Тому що для кожного завдання спосіб розміщення мурах є визначальним. Або всі вони поміщаються в одну точку, або в різні з повтореннями, або без повторень.
    • На цьому ж етапі задається початковий рівень феромону. Він инициализируется невеликим позитивним числом для того, щоб на початковому етапі ймовірності переходу в наступну вершину були нульовими.
  2. Шукаємо рішення.
  3. Оновлюємо феромон.
    • Рівень феромона оновлюється відповідно до наведеної формулою:

      • 1245

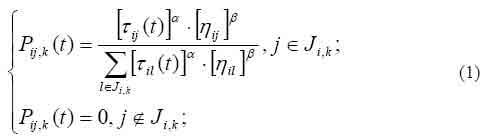
      Де - інтенсивність випаровування, L (t) - ціна поточного рішення для k-ого мурашки, а Q - параметр, що має значення порядку ціни оптимального рішення, тобто - феромон, що відкладається k -м мурахою, викользующім ребро (i, j).

  4. Додаткові дії.
    • Зазвичай тут використовується алгоритм локального пошуку, проте він може також з'явитися і після пошуку всіх рішень.

3.5 Етапи вирішення завдань за допомогою мурашиних алгоритмів

Для того щоб побудувати відповідний мурашиний алгоритм для вирішення якої-небудь задачі, потрібно:

Також визначальними є:

4 РОЇВ МЕТОД ВИЗНАЧЕННЯ ОБ'ЄКТІВ НА ЗОБРАЖЕННІ ЗА ДОПОМОГОЮ АЛГОРИТМА МУРАШНОЇ КОЛОНІЙ

завдання формулюється як задача пошуку мінімального за вартістю амкнутого маршруту по всіх вершин без повторень на повному зваженому графі з n вершинами. Змістовно вершини графа є містами, які повинен відвідати комівояжер, а ваги ребер відображають відстані (довжини) або вартості проїзду. Це завдання є NP-важкою, і точний переборний алгоритм її рішення має факторіальною складність.

Моделювання поведінки мурах пов'язано з розподілом феромону на стежці - ребрі графа в задачі комівояжера. При цьому ймовірність включення ребра в маршрут окремого мурашки пропорційна кількості феромону на цьому ребрі, а кількість відкладали феромона пропорційно довжині маршруту. Чим коротше маршрут, тим більше феромона буде відкладено на його ребрах, отже, більшу кількість мурах буде включати його в синтез власних маршрутів. Моделювання такого підходу, що використовує тільки позитивний зворотний зв'язок, призводить до передчасної збіжності - більшість мурашок рухається по локально оптимальним маршрутом. Уникнути цього можна, моделюючи негативний зворотний зв'язок у вигляді випаровування феромону. При цьому якщо феромон випаровується швидко, то це призводить до втрати пам'яті колонії і забування хороших рішень, з іншого боку, великий час випаровування може привести до отримання стійкого локального оптимального рішення.

Тепер з урахуванням особливостей задачі комівояжера, ми можемо описати локальні правила поведінки мурах при виборі шляху.

  1. Мурахи мають власну пам'ять. Оскільки кожне місто може бути відвіданий тільки один раз, то у кожного мурашки є список вже відвіданих міст - список заборон. Позначимо через список міст, які необхідно відвідати мурашки k, що знаходиться в місті i.
  2. Мурахи мають зором - видимість є евристичне бажання відвідати місто j, якщо мураха знаходиться в місті i. Будемо вважати, що видимість обернено пропорційна відстані між містами.
  3. Мурахи мають нюхом - вони можуть вловлювати слід феромона, що підтверджує бажання відвідати місто j з міста i на підставі досвіду інших мурах. Кількість феромону на ребрі (i, j) в момент часу t позначимо через.
  4. 4. На цій підставі ми можемо сформулювати вероятностно-пропорційне правило, що визначає ймовірність переходу k-ого мурашки з міста i в місто j:

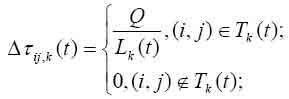
    Де, - параметри, що задають ваги сліду феромону. При = 0 алгоритм вироджується до жодного алгоритму (буде обраний найближче місто). Зауважимо, що вибір міста є імовірнісним, правило (1) лише визначає ширину зони міста j; в загальну зону всіх міст кидається випадкове число, яке і визначає вибір мурашки. Правило (1) не змінюється в ході алгоритму, але у двох різних мурах значення ймовірності переходу будуть відрізнятися, тому що вони мають різний список дозволених міст.

  5. 5. Пройшовши ребро (i, j), мураха відкладає на ньому деяку кількість феромону, яке повинно бути пов'язано з оптимальністю зробленого вибору. Нехай є маршрут, пройдений мурахою k до моменту часу t, - довжина цього маршруту, а Q - параметр, що має значення порядку довжини оптимального шляху. Тоді відкладається кількість феромону може бути задано у вигляді:

    Правила зовнішнього середовища визначають, в першу чергу, випаровування феромону. Нехай є коефіцієнт випаровування, тоді правило випаровування має вигляд:

    де m - кількість мурах в колонії.

На початку алгоритму кількості феромону на ребрах приймається рівним невеликого позитивного числа. Загальна кількість мурах залишається постійним і рівним кількості міст, кожен мураха починає маршрут зі свого міста.

Додаткова модифікація алгоритму може складатися у веденні так званих елітних мурах, які підсилюють ребра Наїлучшего маршруту, знайденого з початку роботи алгоритму. Позначимо через T * найкращий поточний маршрут, через L * - його довжину. Тоді якщо в колонії є e елітних мурах, то ребра маршруту отримають додаткову кількість феромону

4.1 Мурашиний алгоритм для задачі комівояжера в псевдокоді

алгоритм:

Складність даного алгоритму, як нескладно помітити, залежить від часу життя колонії () міст (n) і кількості мурах в колонії (m).

5 МОДИФІКАЦІЯ АЛГОРИТМУ МУРАШНОЇ КОЛОНІЙ ДЛЯ ВИЗНАЧЕННЯ ОБ'ЄКТА НА ЗОБРАЖЕННІ

Оскільки в основі мурашиного алгоритму лежить моделювання пересування мурашок по деяких шляхів, то такий підхід може стати ефективним способом пошуку раціональних рішень для задач оптимізації, що допускають графову інтерпретацію. Ряд експериментів показує, що ефективність мурашиних алгоритмів зростає зі зростанням розмірності вирішуваних завдань оптимізації. Гарні результати виходять для нестаціонарних систем із змінними в часі параметрами, наприклад, для розрахунків телекомунікаційних і комп'ютерних мереж. В Інтернеті можна знайти опис застосування мурашиного алгоритму для розробки оптимальної структури знімальних мереж GPS в рамках створення високоточних геодезичних і знімальних технологій. В даний час на основі застосування мурашиних алгоритмів отримані хороші результати для таких складних оптимізаційних задач, як задача комівояжера, транспортна задача, задача календарного планування, завдання розмальовки графа, квадратична задача про призначення, завдання оптимізації мережевих трафіків і ряд інших.

Якість одержуваних рішень багато в чому залежить від настроювальних параметрів в вероятностно- пропорційному правилі вибору шляху на основі поточної кількості феромону і від параметрів правил відкладання і випаровування фе Ромон. Можливо, що динамічна адаптаційна налаштування цих параметрів може сприяти отриманню кращих рішень. Важливу роль відіграє і початковий розподіл феромона, а також вибір умовно оптимального рішення на кроці ініціалізації.

Перспективними шляхами поліпшення мурашиних алгоритмів є різні адаптації параметрів з використанням бази нечітких правил і їх гібридизація, наприклад, з генетичними алгоритмами. Як варіант, така гібридизація може складатися в обміні через певні проміжки часу поточними найкращими рішеннями.

5.1 Переваги

5.2 Недоліки

ВИСНОВКИ

Мурашині алгоритми засновані на імітації самоорганізації соціальних комах за допомогою використання динамічних механізмів, за допомогою яких система дост Гаета глобальної мети в результаті локального низкоуровневого взаємодії елементів. Ефективність мурашиних алгоритмів збільшується зі зростанням розмірності задачі оптимізації. Мурашині алгоритми забезпечують рішення і дІНШІ комбінаторних задач не гірше загальних метаеврістіческіе технологій оптимізації та деяких проблемно-орієнтованих методів. Особливо хороші результати мурашиної оптимізації виходять для нестаціонарних систем, параметри яких змінюються в часі, наприклад телекомунікаційних і комп'ютерних мереж. Важливою властивістю мурашиних алгоритмів є неконвергентность: навіть після великої кількості ітерацій одночасно досліджується безліч варіантів рішення, внаслідок чого не відбувається тривалих тимчасових затримок в локальних екстремуму. Все це дозволяє рекомендувати застосування мурашиних алгоритмів для вирішення складних комбінаторних задач оптимізації. Перспективними шляхами поліпшення мурашиних алгоритмів є online адаптація параметрів за допомогою бази нечітких правил, а також їх гібридизація з іншими методами природних обчислень, наприклад генетичними алгоритмами.

Список джерел

  1. Вадим Конушін, Володимир Вежневець, Методи сегментації зображень: інтерактивна сегментація, // Вісник МДУ ім Ломоносова - №4, 2008. - С. 107-118
  2. L. Lucchese and S.K. Mitra Color Image Segmentation: A State-of-the-Art Survey, 2001
  3. N. R. Pal and S. K. Pal, A Review on Image Segmentation Techniques, Pattern Recognition, Vol. 26, No 9, 2000.
  4. R. Laptik, D. Navakauskas, Application of Ant Colony Optimization for Image Segmentation [Електронний ресурс]. - Режим доступу: http: //www.ktu .lt / lt / mokslas / ....
  5. Ruobing Zou, Weiyu Yu, Image Segmentation Based on Local Ant Colony Optimization [Електронний ресурс]. - Режим доступу: http://www.computer.org/portal/web/csdl/ ....
  6. Ахметшин А.М., Ахметшина Л.Г., Сегментація низькою контрастністю медичних радіологічних зображень методом просторово-резонансного відображення [Електронний ресурс]. - Режим доступу: http: //www.uacm.kharkov.ua/download / ....
  7. Tomas Piatrik, Ebroul Izquierdo, An application of ant colony optimization to image clustering [Електронний ресурс]. - Режим доступу: http: // citeseerx.ist.psu.edu / ....
  8. Dzung L.Pham, Chenyang Xu, Jerry L.Prince, A survey of current methods in medical image segmentation [Електронний ресурс]. - Режим доступу: http: //www.mcs.csueastbay.edu / ... .
  9. Huizhi Cao, Peng Huang, Shuqian Luo, A novel image segmentation algorithm based on artificial ant colonies [Електронний ресурс]. - Режим доступу: http://books.google.ru/ .. ..
  10. Myung-Eun Lee, Soo-Hyung Kim, Wan-Hyun Cho, Soon-Young Park, Jun-Sik Lim, Segmentation of Brain MR Images Using an Ant Colony Optimization Algorithm [ Електронний ресурс]. - Режим доступу: http://www.computer.org/....